Hvad er en overspringsliste?
En overspringsliste er en probabilistisk datastruktur. Overspringslisten bruges til at gemme en sorteret liste over elementer eller data med en sammenkædet liste. Det gør det muligt at se processen med elementerne eller dataene effektivt. I et enkelt trin springer den flere elementer af hele listen over, hvorfor den er kendt som en overspringsliste.
Overspringslisten er en udvidet version af den sammenkædede liste. Det giver brugeren mulighed for at søge, fjerne og indsætte elementet meget hurtigt. Den består af en basisliste, der inkluderer et sæt elementer, som opretholder linkhierarkiet for de efterfølgende elementer.
Skip listestruktur over
Den er bygget i to lag: Det nederste lag og det øverste lag.
Det nederste lag på overspringslisten er en almindelig sorteret sammenkædet liste, og de øverste lag på overspringslisten er som en 'ekspreslinje', hvor elementerne springes over.
Kompleksitetstabel for Skip-listen
| Ja Nej | Kompleksitet | Gennemsnitligt tilfælde | Værste tilfælde |
|---|---|---|---|
| 1. | Adgang til kompleksitet | O(logn) | På) |
| 2. | Søgekompleksitet | O(logn) | På) |
| 3. | Slet kompleksitet | O(logn) | På) |
| 4. | Indsæt kompleksitet | O(logn) | På) |
| 5. | Rumkompleksitet | - | O(nlogn) |
Overspringslistens arbejde
Lad os tage et eksempel for at forstå, hvordan overspringslisten fungerer. I dette eksempel har vi 14 noder, sådan at disse noder er opdelt i to lag, som vist i diagrammet.
Det nederste lag er en fælles linje, der forbinder alle noder, og det øverste lag er en ekspreslinje, der kun forbinder hovedknuderne, som du kan se i diagrammet.
Antag, at du vil finde 47 i dette eksempel. Du starter søgningen fra den første knude på ekspreslinjen og fortsætter med at køre på ekspreslinjen, indtil du finder en node, der er lig med 47 eller mere end 47.
Du kan se i eksemplet, at 47 ikke findes i ekspreslinjen, så du søger efter en node på mindre end 47, hvilket er 40. Nu går du til den normale linje ved hjælp af 40 og søger på 47, som vist i diagrammet.
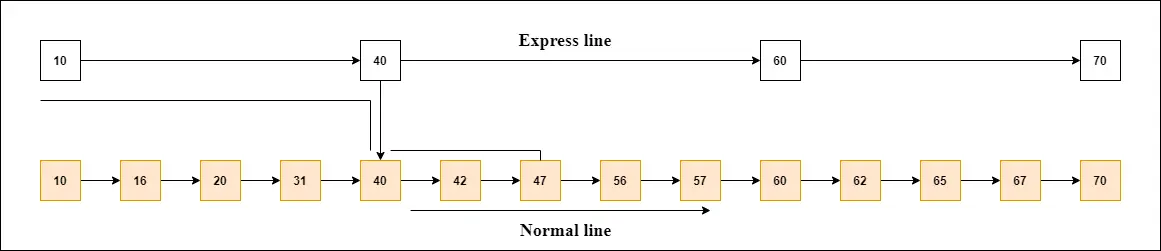
Bemærk: Når du finder en node som denne på 'ekspreslinjen', går du fra denne node til en 'normal bane' ved hjælp af en markør, og når du søger efter knudepunktet i den normale linje.
Spring over liste grundlæggende handlinger
Der er følgende typer operationer i overspringslisten.
Algoritme for indsættelsesoperationen
Insertion (L, Key) local update [0...Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] lvl = random_Level() if lvl > L → level then for i = L → level + 1 to lvl do update[i] = L → header L → level = lvl a = makeNode(lvl, Key, value) for i = 0 to level do a → forward[i] = update[i] → forward[i] update[i] → forward[i] = a
Algoritme for sletningsoperation
Deletion (L, Key) local update [0... Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] if a → key = Key then for i = 0 to L → level do if update[i] → forward[i] ? a then break update[i] → forward[i] = a → forward[i] free(a) while L → level > 0 and L → header → forward[L → level] = NIL do L → level = L → level - 1
Algoritme for søgeoperation
Searching (L, SKey) a = L → header loop invariant: a → key level down to 0 do. while a → forward[i] → key forward[i] a = a → forward[0] if a → key = SKey then return a → value else return failure
Eksempel 1: Opret en overspringningsliste, vi ønsker at indsætte disse følgende nøgler i den tomme overspringningsliste.
- 6 med niveau 1.
- 29 med niveau 1.
- 22 med niveau 4.
- 9 med niveau 3.
- 17 med niveau 1.
- 4 med niveau 2.
Flere år:
Trin 1: Indsæt 6 med niveau 1

Trin 2: Indsæt 29 med niveau 1

Trin 3: Indsæt 22 med niveau 4

Trin 4: Indsæt 9 med niveau 3

Trin 5: Indsæt 17 med niveau 1

Trin 6: Indsæt 4 med niveau 2

Eksempel 2: Overvej dette eksempel, hvor vi vil søge efter nøgle 17.

Flere år:

Fordele ved Skip-listen
- Hvis du ønsker at indsætte en ny node i overspringslisten, så indsætter den noden meget hurtigt, fordi der ikke er nogen rotationer i overspringslisten.
- Overspringslisten er enkel at implementere sammenlignet med hash-tabellen og det binære søgetræ.
- Det er meget nemt at finde en node på listen, fordi den gemmer noderne i sorteret form.
- Overspringslistealgoritmen kan meget nemt ændres i en mere specifik struktur, såsom indekserbare overspringslister, træer eller prioritetskøer.
- Overspringslisten er en robust og pålidelig liste.
Ulemper ved Skip-listen
- Det kræver mere hukommelse end det balancerede træ.
- Omvendt søgning er ikke tilladt.
- Overspringslisten søger i noden meget langsommere end den sammenkædede liste.
Anvendelser af skipningslisten
- Det bruges i distribuerede applikationer, og det repræsenterer pointerne og systemet i de distribuerede applikationer.
- Det bruges til at implementere en dynamisk elastisk samtidig kø med lav låsekonflikt.
- Det bruges også sammen med QMap-skabelonklassen.
- Indekseringen af overspringslisten bruges til at køre medianproblemer.
- Overspringslisten bruges til delta-kodningsposteringen i Lucene-søgningen.
