I datalogi findes der nogle problemer, hvis løsninger endnu ikke er fundet, problemerne er opdelt i klasser kendt som Kompleksitetsklasser . I kompleksitetsteori er en kompleksitetsklasse et sæt problemer med relateret kompleksitet. Disse klasser hjælper videnskabsmænd med at gruppere problemer baseret på, hvor meget tid og plads de kræver for at løse problemer og verificere løsningerne. Det er grenen af teorien om beregning, der beskæftiger sig med de ressourcer, der kræves for at løse et problem.
forskel mellem program og script
De fælles ressourcer er tid og rum, hvilket betyder, hvor meget tid algoritmen tager at løse et problem og den tilsvarende hukommelsesbrug.
- Tidskompleksiteten af en algoritme bruges til at beskrive antallet af trin, der kræves for at løse et problem, men den kan også bruges til at beskrive, hvor lang tid det tager at verificere svaret.
- Rumkompleksiteten af en algoritme beskriver, hvor meget hukommelse der kræves for at algoritmen kan fungere.
Kompleksitetsklasser er nyttige til at organisere lignende typer problemer.
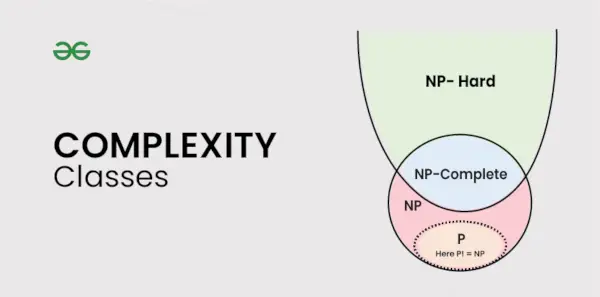
Typer af kompleksitetsklasser
Denne artikel diskuterer følgende kompleksitetsklasser:
- P klasse
- NP klasse
- CoNP klasse
- NP-hårdt
- NP-komplet
P klasse
P'et i P-klassen står for Polynomisk tid. Det er samlingen af beslutningsproblemer (problemer med et ja eller nej svar), der kan løses af en deterministisk maskine i polynomisk tid.
Funktioner:
- Løsningen til P problem s er let at finde.
- P er ofte en klasse af beregningsmæssige problemer, der kan løses og løses. Tractable betyder, at problemerne kan løses i teorien såvel som i praksis. Men de problemer, der kan løses i teorien, men ikke i praksis, er kendt som uløselige.
Denne klasse indeholder mange problemer:
- Beregning af den største fælles divisor.
- At finde en maksimal matchning.
- Flet sortering
NP klasse
NP i NP-klassen står for Ikke-deterministisk polynomisk tid . Det er samlingen af beslutningsproblemer, der kan løses af en ikke-deterministisk maskine i polynomisk tid.
streng til int i java
Funktioner:
- NP-klassens løsninger er svære at finde, da de løses af en ikke-deterministisk maskine, men løsningerne er nemme at verificere.
- Problemer med NP kan verificeres af en Turing-maskine i polynomiel tid.
Eksempel:
Lad os overveje et eksempel for bedre at forstå NP klasse . Antag, at der er en virksomhed, der har i alt 1000 medarbejdere har en unik medarbejder ID'er . Antag, at der er 200 ledige værelser for dem. Et udvalg af 200 medarbejdere skal være parret sammen, men den administrerende direktør i virksomheden har data fra nogle medarbejdere, der ikke kan arbejde i samme rum på grund af personlige årsager.
Dette er et eksempel på en F.EKS problem. Da det er nemt at tjekke om det givne valg af 200 medarbejdere foreslået af en kollega er tilfredsstillende eller ej, dvs. intet par taget fra kollegalisten vises på listen givet af den administrerende direktør. Men at generere en sådan liste fra bunden ser ud til at være så svært, at det er fuldstændig upraktisk.
Det indikerer, at hvis nogen kan give os løsningen på problemet, kan vi finde det rigtige og forkerte par i polynomisk tid. Således for F.EKS klasseproblem, er svaret muligt, som kan beregnes i polynomisk tid.
Denne klasse indeholder mange problemer, som man gerne vil kunne løse effektivt:
- Boolean Satisfiability Problem (SAT).
- Hamiltonsk vejproblem.
- Graffarvning.
Co-NP klasse
Co-NP står for komplementet til NP-klassen. Det betyder, at hvis svaret på et problem i Co-NP er Nej, så er der bevis, der kan kontrolleres i polynomisk tid.
Funktioner:
- Hvis et problem X er i NP, så er dets komplement X' også i CoNP.
- For et NP- og CoNP-problem er der ikke behov for at verificere alle svarene på én gang i polynomisk tid, der er behov for kun at verificere et bestemt svar ja eller nej i polynomiumtid for at et problem skal være i NP eller CoNP.
Nogle eksempler på problemer for CoNP er:
- For at kontrollere primtal.
- Heltalsfaktorisering.
NP-hård klasse
Et NP-hårdt problem er mindst lige så svært som det sværeste problem i NP, og det er en klasse af problemer, således at hvert problem i NP reduceres til NP-hårdt.
Funktioner:
- Alle NP-hårde problemer er ikke i NP.
- Det tager lang tid at tjekke dem. Det betyder, at hvis der gives en løsning på et NP-hårdt problem, så tager det lang tid at kontrollere, om det er rigtigt eller ej.
- Et problem A er i NP-hårdt, hvis der for hvert problem L i NP eksisterer en polynomisk tidsreduktion fra L til A.
Nogle af eksemplerne på problemer i Np-hard er:
java version linux
- Stoppe problem.
- Kvalificerede booleske formler.
- Ingen Hamilton-cyklus.
NP-komplet klasse
Et problem er NP-komplet, hvis det både er NP og NP-hårdt. NP-komplette problemer er de svære problemer i NP.
Funktioner:
- NP-komplette problemer er specielle, da ethvert problem i NP-klassen kan transformeres eller reduceres til NP-komplette problemer i polynomisk tid.
- Hvis man kunne løse et NP-fuldstændigt problem i polynomiel tid, så kunne man også løse et hvilket som helst NP-problem i polynomiel tid.
Nogle eksempler på problemer omfatter:
- Hamiltonsk cyklus.
- Tilfredsstillende.
- Vertex dæksel .
| Klasse kompleksitet | Karakteristisk træk |
| P | Let opløselig i polynomiel tid. |
| F.EKS | Ja, svar kan kontrolleres i polynomiel tid. |
| Co-NP | Nej, svar kan kontrolleres i polynomiel tid. |
| NP-hårdt | Alle NP-hårde problemer er ikke i NP, og det tager lang tid at tjekke dem. |
| NP-komplet | Et problem, der er NP og NP-hårdt, er NP-komplet. |
