NEWTONS LOV OM AFKØLING: DEFINITION, BEVIS, FORMLER OG EKSEMPLER

Newtons lov om afkøling er den grundlæggende lov, der beskriver hastigheden af varmeoverførsel fra et legeme til dets omgivelser gennem stråling. Denne lov siger, at den hastighed, hvormed kroppen udstråler varme, er direkte proportional med forskellen i kroppens temperatur fra dens omgivelser, givet at forskellen i temperatur er lav. dvs. jo højere forskellen er mellem temperaturen på kroppen og dens omgivelser, jo mere varme går der tabt, og jo lavere temperatur, jo mindre varme går der tabt. Newtons lov om afkøling er et specialtilfælde af Stefan-Boltzmanns lov.

I denne artikel vil vi lære om Newtons lov om afkøling, Newtons lov om afkøling, dens afledning, eksempler og andre i detaljer.

Definition af Newtons lov om afkøling

Newton var den første til at studere forholdet mellem den varme, et legeme tabte til dets omgivelser. Han siger, at jo større forskel i temperaturen mellem objektet og dets omgivelser, jo mere varme udstråles af kroppen.

Newtons lov om afkøling anfører, at

Satsen for varmetab fra en krop er direkte proportional med forskellen i temperatur mellem kroppen og dens omgivelser, givet at temperaturforskellen ikke er stor.

Denne lov bruges til at forklare, hvorfor varmt vand eller mælk efterladt på et bord afkøles hurtigere end lidt varm mælk eller vand tilbage på bordet. Newtons lov om afkøling hjælper os med at måle temperaturen på nogen uden faktisk at måle den, givet kroppens begyndelsestemperatur og omgivelsernes temperatur.

Newtons lov om køleformel

Newtons lov om køleformel er en formel til at beregne temperaturen af et materiale, da det taber varme til dets omgivelser gennem stråling.

Ifølge Newtons lov om afkøling,

Satsen for tab af varme ( – dQ/dt) af kroppen er direkte proportional med forskellen i temperatur [ΔT = (T ₂ – T ₁ )] af kroppen og omgivelserne.

gør mens du er i java

Vi kan repræsentere det som

– dQ/dt ∝ (T ₂ – T ₁ )

– dQ/dt = k(T ₂ – T ₁ )

hvor,
k er en proportionalitetskonstant

Ved at løse ovenstående differentialligning får vi,

T(t) = T _s + (T _O – T _s ) Det er ^-kt

hvor,
t er tiden
T(t) er kroppens temperatur på tidspunktet t
T _s er den omgivende temperatur
T _O er kroppens begyndelsestemperatur
k er proportionalitetskonstanten

Afledning af Newtons lov om afkøling

Newtons lov om afkøling kan udledes ved hjælp af løsningen af differentialligningen. Lad et legeme med massen m, med specifik varmekapacitet s, have temperatur T₂og T₁er omgivelsernes temperatur.

Hvis temperaturen falder med en lille mængde dT ₂ i tide dt , så er mængden af tabt varme,

dQ = ms dT ₂

Hastighed for tab af varme er givet ved,

dQ/dt = ms (dT ₂ /dt)

Ifølge Newtons lov om afkøling,

– dQ/dt = k(T ₂ – T ₁ )

Sammenligning af ovenstående ligning

– ms (dT ₂ /dt) = k (T ₂ – T ₁ )

dT ₂ /(T ₂ –T ₁ ) = – (k / ms) dt

dT ₂ /(T ₂ – T ₁ ) = – Kdt

hvor, K = k/m s

Integration af ovenstående ligning

log _{det er} (T ₂ – T ₁ ) = – K t + c

T ₂ = T ₁ + C' og ^–Kt

hvor, C' = e ^c

Forholdet mellem faldet i kroppens temperatur og tiden vises ved hjælp af afkølingsgrafen. Hældningen af denne graf viser temperaturens faldhastighed.

Kølekurven er en graf, der viser sammenhængen mellem kropstemperatur og tid. Temperaturfaldets hastighed bestemmes af hældningen af tangenten til kurven på ethvert punkt. Billedet tilføjet nedenfor viser temperaturfald og tidsforhold.

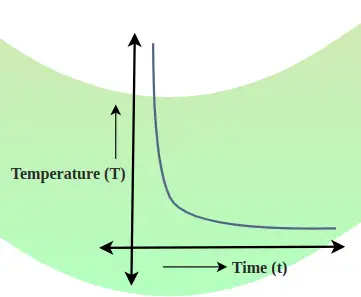
Generelt,

T(t) = T _EN +(T _H -T _EN )Det er ^-kt

hvor
T(t) er temperaturen på tidspunktet t
T _EN er omgivelsernes omgivelsestemperatur eller temperatur
T _H er temperaturen på den varme genstand
k er den positive konstant og t er tiden

Metoder til at anvende Newtons lov om afkøling

Ved en konstant afkølingshastighed er afkølingshastigheden relateret til kroppens gennemsnitlige temperatur i intervallet, så kan vi beregne den omtrentlige værdi ved hjælp af Newtons lov om afkøling

dθ/dt = k(q – q _s )

hvor,
q er kroppens temperatur
q _s er temperaturen i omgivelserne

Hvis kroppens gennemsnitlige temperatur er q, hvor

java int til streng

q = (q _jeg + q _f )/2

Verifikation af Newtons lov om afkøling

Vi kan nemt verificere Newtons lov om afkøling ved eksperimentet beskrevet nedenfor:

I forsøget tager vi et dobbeltvægget kar (V) med vand i mellem de to vægge. Inde i det dobbeltvæggede kar tager vi et kobberkalorimeter (C) indeholdende varmt vand.

Vi bruger to termometre T₂at måle temperaturen på vandet i kalorimeteret og T₁at måle temperaturenaf det varme vand mellem de dobbelte vægge. Efter lige store tidsintervaller noteres begge temperaturer og en graf mellem loggen_{det er}(T₂–T₁) og tiden (t) er plottet, der vises som en ret linje med negativ hældning.

Newtons lov om afkøling graf

Grafen for Newtons lov om afkøling er tilføjet nedenfor, i denne graf er log over forskellen mellem de to temperaturer og tiden vist.

Begrænsninger af Newtons lov om afkøling

Forskellige begrænsninger af Newtons lov om afkøling er,

Newtons lov om afkøling gælder, hvis temperaturforskellen mellem kroppen og miljøet er lille.

Kroppens varmetab er kun i form af Stråling .

Temperaturen i omgivelserne skal forblive konstant under afkølingen af kroppen, hvis ikke, så holder Newtons lov om afkøling ikke.

Anvendelser af Newtons lov om afkøling

Forskellige anvendelser af Newtons lov om afkøling er,

At vurdere, hvor lang tid en varm genstand vil tage om at køle ned til en bestemt temperatur.

At bestemme temperaturen på en drink i et køleskab, efter at der er gået et bestemt tidsrum.

Det hjælper med at angive dødstidspunktet ved at se på den mulige kropstemperatur på dødstidspunktet og den aktuelle kropstemperatur.

Læs mere,

Specifik varmekapacitet

Grundlæggende koncept for termodynamik

Termodynamiske processer

Løste eksempler Newtons lov om afkøling

Eksempel 1: En pande fyldt med varm mad afkøles fra 94 °C til 86 °C på 2 minutter, når rumtemperaturen er på 20 °C. Hvor lang tid tager det at afkøle fra 71 °C til 69 °C?

Løsning:

Gennemsnit på 94 °C og 86 °C er 90 °C,

T₂= 90 °C

T₁= 20 °C

Drop in tem. mad er 8 °C på 2 minutter.

Ifølge Newtons lov om afkøling,

– dQ/dt = k(T ₂ –T ₁ )

8 °C /2 min = k(90 – 20)

4 = k(70) …………(1)

Gennemsnit på 69 °C og 71 °C er 70 °C

T₂= 70 °C

T₁= 20 °C

Ifølge Newtons lov om afkøling,

2 °C/dt = k(70 – 20) ……(2)

Fra ligning (1) og (2),

Ændring i tid = 0,7 min = =42 sek

Maden vil således tage 42 sekunder at afkøle fra 71 °C til 69 °C.

Eksempel 2: Et legeme ved en temperatur på 40ºC holdes i omgivelser med en konstant temperatur på 20ºC. Det observeres, at dens temperatur falder til 35ºC på 10 minutter. Find ud af, hvor meget mere tid det tager for kroppen at opnå en temperatur på 30ºC.

Løsning:

hvad er 10 af 100

givet,

q_jeg= (40 – 20)ºC

q_f= (35 – 20)ºC

Ifølge Newtons lov om afkøling

q _f = q _jeg det er ^-kt

Nu, for det interval, hvor temperaturen falder fra 40 ºC til 35 ºC.

(35 – 20) = (40 – 20) og^-(10k)

det er^-10k= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

Bruger nu Newons formel igen,

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

det er^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

Ved at bruge værdien af k,

t = 0,40546/0,02876

t = 14,098 min

Således er den tid, det tager kroppen at nå temperaturen på 30ºC, 14.098 min.

Eksempel 3: Olien opvarmes til 70 ºC. Den afkøles til 50 ºC efter 6 minutter. Beregn den tid, det tager olien at afkøle fra 50 ºC til 40 ºC givet den omgivende temperatur T _s = 25 ºC

Løsning:

givet,

Oliens temperatur efter 6 minutter, dvs. T(t) er lig med 50 ºC

Omgivelsestemperatur T_s= 25 ºC

Temperatur af olie, T_O= 70 ºC

Tid til afkøling til 50ºC = 6 min

Ifølge Newtons lov om afkøling,

T(t) = T_s+ (T₀– T_s) Det er^-kt

{T(t) – T_s}/(T_O– T_s) = og^-kt

-kt = ln[(T(t) – T_s)/(T_O– T_s)] ………(1)

Erstat værdierne

-kt = ln[(50 – 25)/(70 – 25)]

-k = (ln 0,55556)/6

k = 0,09796
maven installere

Gennemsnitstemperatur fra 50 ºC til 40 ºC er lig med 45 ºC

Igen ved at bruge Newtons lov om afkøling

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8,278 min

Den tid, det tager olie at køle fra 50 ºC til 40 ºC, er således 8,278 min

Eksempel 4: Vand opvarmes til 80 ºC i 10 min. Hvor meget ville dens temperatur i grader Celsius være, hvis k = 0,056 pr. min og den omgivende temperatur er 25 ºC?

Løsning:

givet,

Omgivelsestemperatur T_s= 25 ºC

Vandets temperatur T₀= 80 ºC

Tid, hvori vand opvarmes (t) = 10 min

Værdi af konstant k = 0,056.

Ifølge Newtons lov om afkøling,
25 af 100

T(t) = T_s+ (T₀– T_s) Det er^-kt

Erstatning af værdien

T(t)= 25 + (80 – 25)e^-(0,056×10)

T(t) = 25 + 55 e^-(0,056×10)

T(t) = 25 + 31,42

T(t) = 56,42

Efter 10 minutter ville vandtemperaturen være 56,42 ºC.

Ofte stillede spørgsmål om Newtons lov om køling

Q1: Hvad er Newtons lov om afkøling?

Svar:

Newtons lov om afkøling siger, at en krops varmetabshastighed er direkte proportional med forskellen i temperatur mellem kroppen og dens omgivelser.

Q2: Hvad er Newtons lov om køleformel?

Svar:

Newtons lov om afkøling siger, at

T(t) = T _s + (T _O – T _s ) Det er ^-kt

Q3: Hvad er k i Newtons lov om afkøling?

Svar:

Det k i Newtons lov om afkøling er den konstant, der afhænger af materialet, dvs. ændring af materialet ændrer k i Newtons lov om afkøling.

Spørgsmål 4: Hvorfor er varm mælk nemmere at drikke fra en skål end fra et glas?

Svar:

Skålen har et større overfladeareal end glas, derfor taber mere varme til omgivelserne i form af varmestråling gennem skålen og dermed er det nemmere for os at drikke varm mælk fra skålen.