Luhn-algoritmen, også kendt som modul 10 eller mod 10 algoritme, er en simpel kontrolsumformel, der bruges til at validere en række identifikationsnumre, såsom kreditkortnumre, IMEI-numre, canadiske socialforsikringsnumre. LUHN-formlen blev skabt i slutningen af 1960'erne af en gruppe matematikere. Kort efter vedtog kreditkortselskaber det. Fordi algoritmen er i det offentlige domæne, kan den bruges af alle. De fleste kreditkort og mange offentlige identifikationsnumre bruger algoritmen som en simpel metode til at skelne gyldige numre fra forkert indtastede eller på anden måde forkerte numre. Det er designet til at beskytte mod utilsigtede fejl, ikke ondsindede angreb.
Trin involveret i Luhn-algoritmen
Lad os forstå algoritmen med et eksempel:
Overvej eksemplet med et kontonummer 79927398713 .
Trin 1 – Startende fra cifferet længst til højre, fordoble værdien af hvert andet ciffer,
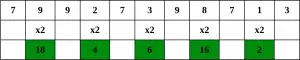
Trin 2 – Hvis fordobling af et tal resulterer i et tocifret tal, dvs. større end 9 (f.eks. 6 × 2 = 12), skal du tilføje cifrene for produktet (f.eks. 12: 1 + 2 = 3, 15: 1 + 5 = 6), for at få et enkeltcifret nummer.

Trin 3 – Tag nu summen af alle cifrene.
hvad er dvale

Trin 4 – Hvis den samlede modulo 10 er lig med 0 (hvis totalen ender på nul), er tallet gyldigt i henhold til Luhn-formlen; ellers er det ikke gyldigt.

Da summen er 70, hvilket er et multiplum af 10, er kontonummeret muligvis gyldigt.
Ideen er enkel; vi krydser fra enden. For hvert andet ciffer fordobler vi det, før vi tilføjer det. Vi tilføjer to cifre af tallet opnået efter fordobling.
Implementering:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
applet applet
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
C#
java streng formatering
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)> >{> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
>
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
forekomst af java
>
>Produktion
This is a valid card>
Luhn-algoritmen registrerer enhver enkeltcifret fejl såvel som næsten alle transpositioner af tilstødende cifre.
