Lineær programmering er et matematisk begreb, der bruges til at finde den optimale løsning af den lineære funktion. Denne metode bruger simple antagelser til at optimere den givne funktion. Lineær programmering har en enorm applikation i den virkelige verden, og den bruges til at løse forskellige typer problemer.
Lineær programmering bruges i forskellige industrier såsom shippingindustrier, fremstillingsindustrier, transportindustrier, telekommunikation og andre.
Term lineær programmering består af to ord lineær og programmering, ordet lineær fortæller forholdet mellem forskellige typer variabler af grad en brugt i et problem, og ordet programmering fortæller os den trinvise procedure til at løse disse problemer.
I denne artikel lærer vi mere om lineær programmering, dens eksempler, formler og andre begreber i detaljer.
Indholdsfortegnelse
- Hvad er lineær programmering?
- Komponenter i lineær programmering
- Eksempler på lineær programmering
- Lineære programmeringsproblemer
- Typer af lineære programmeringsproblemer
- Lineær programmeringsformel
- Hvordan løses lineære programmeringsproblemer?
- Lineære programmeringsmetoder
- Simplex metode til lineær programmering
- Lineær programmering grafisk metode
- Lineære programmeringsapplikationer
- Betydningen af lineær programmering
- Ajourførte anvendelser af lineær programmering
- Lineær programmering i operationsforskning
- Simplex metode
Hvad er lineær programmering?
Lineær programmering eller Lineær optimering er en teknik, der hjælper os med at finde den optimale løsning til et givent problem, en optimal løsning er en løsning, der er det bedst mulige resultat af et givent problem.
Enkelt sagt er det metoden til at finde ud af, hvordan man gør noget bedst muligt. Med begrænsede ressourcer skal du gøre den optimale udnyttelse af ressourcerne og opnå det bedst mulige resultat i et bestemt mål, såsom mindste omkostninger, højeste margin eller mindst tid.
Den situation, der kræver en søgning efter de bedste værdier af variablerne underlagt visse begrænsninger, er, hvor vi bruger lineære programmeringsproblemer. Disse situationer kan ikke håndteres med de sædvanlige beregninger og numeriske teknikker.
Lineær programmeringsdefinition
Lineær programmering er den teknik, der bruges til at optimere et bestemt scenarie. Ved at bruge lineær programmering får vi det bedst mulige resultat i en given situation. Det bruger alle de tilgængelige ressourcer på en måde, så de giver det optimale resultat.
Komponenter i lineær programmering
De grundlæggende komponenter i et lineært programmeringsproblem (LP) er:
- Beslutningsvariabler: Variabler du ønsker at bestemme for at opnå den optimale løsning.
- Målfunktion: M atematisk ligning, der repræsenterer det mål, du ønsker at opnå
- Begrænsninger: Begrænsninger eller restriktioner, som dine beslutningsvariabler skal følge.
- Ikke-negativitetsbegrænsninger: I nogle scenarier i den virkelige verden kan beslutningsvariabler ikke være negative
Yderligere egenskaber ved lineær programmering
- Endelighed: Antallet af beslutningsvariable og begrænsninger i et LP-problem er begrænset.
- Linearitet: Den objektive funktion og alle begrænsninger skal være lineære funktioner af beslutningsvariablerne . Det betyder, at graden af variabler skal være én.
Eksempler på lineær programmering
Vi kan forstå de situationer, hvor lineær programmering anvendes ved hjælp af eksemplet diskuteret nedenfor,
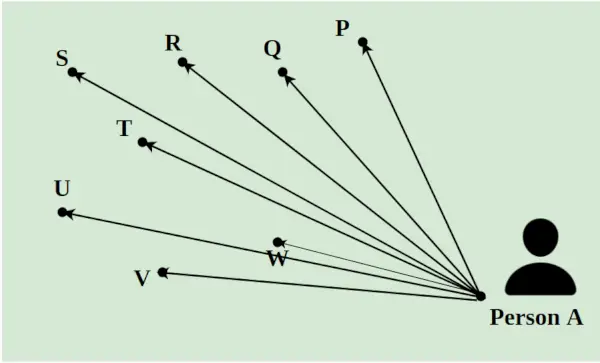
Antag, at en leveringsmand skal levere 8 pakker på en dag til de forskellige steder i en by. Han skal vælge alle pakkerne fra A og skal levere dem til punkterne P, Q, R, S, T, U, V og W. Afstanden mellem dem er angivet ved hjælp af linjerne som vist på billedet nedenfor. Den korteste vej, som leveringsmanden følger, beregnes ved hjælp af konceptet lineær programmering.
lytteport
Lineære programmeringsproblemer
Lineære programmeringsproblemer (LPP) involvere at optimere en lineær funktion for at finde den optimale værdiløsning for funktionen. Den optimale værdi kan enten være maksimumværdien eller minimumsværdien.
I LPP kaldes de lineære funktioner objektive funktioner. En objektiv funktion kan have flere variable, som er underlagt betingelser og skal opfylde lineære begrænsninger .
Typer af lineære programmeringsproblemer
Der er mange forskellige lineære programmeringsproblemer (LPP), men vi vil behandle tre store lineære programmeringsproblemer i denne artikel.
Produktionsproblemer
Produktionsproblemer er et problem, der omhandler antallet af enheder, der skal produceres eller sælges for at maksimere fortjenesten, når hvert produkt kræver fast arbejdskraft, maskintimer og råmaterialer.
Kost problemer
Det bruges til at beregne antallet af forskellige slags bestanddele, der skal inkluderes i kosten for at få minimumsomkostningerne, afhængigt af tilgængeligheden af fødevarer og deres priser.
Transportproblemer
Det bruges til at bestemme transportplanen for at finde den billigste måde at transportere et produkt fra planter/fabrikker beliggende forskellige steder til forskellige markeder.
Lineær programmeringsformel
Et lineært programmeringsproblem består af,
- Beslutningsvariable
- Objektiv funktion
- Begrænsninger
- Ikke-negative begrænsninger
Beslutningsvariable er variablerne x og y, som bestemmer outputtet af det lineære programmeringsproblem og repræsenterer den endelige løsning.
Det objektiv funktion , generelt repræsenteret ved Z, er den lineære funktion, der skal optimeres i henhold til den givne betingelse for at få den endelige løsning.
Det restriktioner pålagt beslutningsvariable, der begrænser deres værdier, kaldes begrænsninger.
Nu er den generelle formel for et lineært programmeringsproblem,
Objektiv funktion : Z = axe + by
Begrænsninger: cx + dy ≥ e, px + qy ≤ r
Ikke-negative begrænsninger: x ≥ 0, y ≥ 0
I ovenstående betingelse er x og y beslutningsvariablene.
Hvordan løses lineære programmeringsproblemer?
Før vi løser de lineære programmeringsproblemer, skal vi først formulere problemerne i henhold til standardparametrene. Trinene til løsning af lineære programmeringsproblemer er,
Trin 1: Marker beslutningsvariablerne i opgaven.
Trin 2: Byg den objektive funktion af problemet og tjek om funktionen skal minimeres eller maksimeres.
Trin 3: Skriv alle begrænsningerne for de lineære problemer ned.
Trin 4: Sikre ikke-negative begrænsninger af beslutningsvariablerne.
Trin 5: Løs nu det lineære programmeringsproblem ved hjælp af en hvilken som helst metode, generelt bruger vi enten den simplekse eller den grafiske metode.
Lineære programmeringsmetoder
Vi bruger forskellige metoder til at løse lineære programmeringsproblemer. De to mest anvendte metoder er,
- Simplex metode
- Grafisk metode
Lad os lære om disse to metoder i detaljer i denne artikel,
Simplex metode til lineær programmering
En af de mest almindelige metoder til at løse det lineære programmeringsproblem er simpleksmetoden. I denne metode gentager vi en specifik betingelse 'n' et antal gange, indtil en optimal løsning er opnået.
De nødvendige trin for at løse lineære programmeringsproblemer ved hjælp af simplex-metoden er,
Trin 1: Formuler de lineære programmeringsproblemer ud fra de givne begrænsninger.
Trin 2: Konverter alle de givne uligheder til ligninger eller ligheder for de lineære programmeringsproblemer ved at tilføje slack-variablen til hver ulighed, hvor det nogensinde er nødvendigt.
Trin 3: Konstruer den indledende simplex-tabel. Ved at repræsentere hver begrænsningsligning i en række og skrive objektivfunktionen i nederste række. Den således opnåede tabel kaldes Simplex-tabellen.
Trin 4: Identificer den største negative indgang i nederste række kolonnen i elementet med den højeste negative indgang kaldes pivotkolonnen
Trin 5: Del indtastningerne i kolonnen længst til højre med indtastningerne i den respektive pivotkolonne, undtagen indtastningerne i den nederste række. Nu kaldes den række, der indeholder den mindste post, pivotrækken. Pivotelementet opnås ved skæringspunktet mellem pivotrækken og pivotkolonnen.
Trin 6: Ved hjælp af matrixdrift og ved hjælp af pivotelementet skal alle indtastninger i pivotkolonnen være nul.
Trin 7: Tjek for de ikke-negative poster i den nederste række, hvis der ikke er negative poster i den nederste række, afslut processen, ellers start processen igen fra trin 4.
Trin 8: Den endelige simplekstabel, der er opnået således, giver løsningen på vores problem.
Lineær programmering grafisk metode
Graphical Method er en anden metode end Simplex-metoden, som bruges til at løse lineære programmeringsproblemer. Som navnet antyder bruger denne metode grafer til at løse de givne lineære programmeringsproblemer. Dette er den bedste metode til at løse lineære programmeringsproblemer og kræver mindre indsats end simpleksmetoden.
Mens vi bruger denne metode, plotter vi alle de uligheder, der er udsat for begrænsninger i de givne lineære programmeringsproblemer. Så snart alle ulighederne for den givne LPP er plottet i XY-grafen, giver den fælles region for alle ulighederne den optimale løsning. Alle hjørnepunkterne i den mulige region beregnes, og værdien af den objektive funktion ved alle disse punkter beregnes, og ved at sammenligne disse værdier får vi den optimale løsning af LPP.
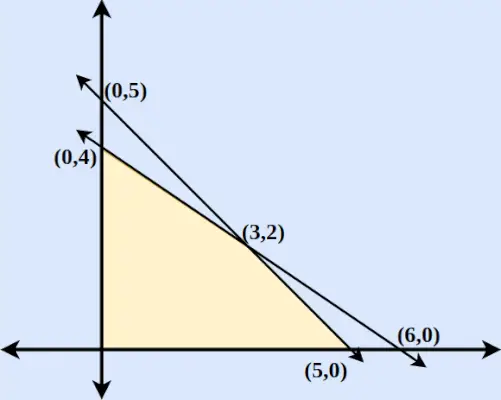
Eksempel: Find den maksimale og minimale værdi af z = 6x + 9y, når begrænsningsbetingelserne er,
- 2x + 3y ≤ 12
- x og y ≥ 0
- x + y ≤ 5
Løsning:
Trin 1 : Konverter først ligningerne til normalligninger. Derfor vil ligningerne være 2x+3y = 0, x = 0, y = 0 og x + y = 5.
Trin 2 : Find de punkter, hvor 2x + 3y og x + y = 5 skærer x-aksen og y-aksen. For at finde skæringspunktet for x-aksen skal du sætte y = 0 i den respektive ligning og finde punktet. Tilsvarende for y-aksens skæringspunkter sættes x = 0 i den respektive ligning.
Trin 3 : Tegn de to linjer, der skærer x-aksen og y-aksen. Vi finder, at de to akser skærer hinanden ved (3,2).
Trin 4 : For x ≥ 0 og y ≥ 0 finder vi, at begge ligninger følges. Derfor vil regionen omfatte et områdeområde omgivet af to akser og begge linjer inklusive oprindelsen. Det plottede område er vist nedenfor i figuren.
Trin 5 : Find Z for hvert punkt og maksima og minima.
Koordinater Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3.2) Z = 36 Derfor finder vi, at Z = 6x + 9y er maksimum ved (0,5) og minimum ved (5,0).
Lineære programmeringsapplikationer
Lineær programmering har applikationer inden for forskellige områder. Det bruges til at finde minimumsomkostningerne ved en proces, når alle problemernes begrænsninger er givet. Det bruges til at optimere transportomkostningerne for køretøjet osv. Forskellige anvendelser af lineær programmering er
Ingeniørindustrien
Engineering Industries bruger lineær programmering til at løse design- og fremstillingsproblemer og for at få det maksimale output fra en given tilstand.
Fremstillingsindustrier
Fremstillingsindustrien bruger lineær programmering for at maksimere virksomhedernes fortjeneste og reducere produktionsomkostningerne.
Energiindustrien
Energiselskaber bruger lineær programmering til at optimere deres produktionsoutput.
Transport industrier
Lineær programmering bruges også i transportindustrien for at finde vejen til at minimere omkostningerne ved transport.
Betydningen af lineær programmering
Lineær programmering har enorm betydning i forskellige industrier, det maksimerer outputværdien, mens inputværdierne minimeres i henhold til forskellige begrænsninger.
LP er yderst anvendelig, når vi har flere betingelser, mens vi løser et problem, og vi skal optimere outputtet af problemet, dvs. enten skal vi finde minimums- eller maksimumværdien i henhold til en given betingelse.
sammenligning af løve og tiger
Læs mere,
- Lineære uligheder
- Algebraisk løsning af lineære uligheder
Lineære programmeringsproblemer
Opgave 1: En virksomhed fremstiller og sælger to typer produkter, og produktionsomkostningerne for hver enhed a og b er henholdsvis 200 og 150 rupees hver enhed produkt giver en fortjeneste på 20 rupees og hver enhed af produkt b giver en fortjeneste på 15 rupees ved salg . Virksomheden estimerer den månedlige efterspørgsel af A og B til maksimalt at være på den høstede enhed i hele produktionsbudgettet for måneden er sat til rupier 50000. Hvor mange enheder skal virksomheden fremstille for at opnå maksimal fortjeneste på sit månedlige salg fra en og b?
Løsning:
Lad x = antallet af enheder af type A
y = Antal enheder af type B
Maksimer Z = 40x + 50y
Med forbehold for begrænsningerne
3x + y ≤ 9
x + 2y ≤ 8
og x, y ≥ 0
Overvej ligningen,
3x + y = 9
x = 3
y = 0
og x + 2y = 8
x = 8
y = 0
Nu kan vi bestemme den maksimale værdi af Z ved at evaluere værdien af Z ved de fire punkter (hjørnepunkter) er vist nedenfor
Toppunkter
Z = 40x + 50y
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Maksimal fortjeneste, Z = Rs. 230
∴ Antal enheder af type A er 2 og antallet af enheder af type B er 3.
Opgave 2: Maksimer Z = 3x + 4y.
Med forbehold for begrænsninger, x + y ≤ 450, 2x + y ≤ 600 og x, y ≤ 0.
Løsning:
Vi har fra det givne
Begrænsninger (1)
X + Y = 450
Sætter x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Sætter y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Fra, Begrænsninger (2)
2x + y = 600
Sætter x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Sætter y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Nu har vi punktkoordinaten Z = 3x + 4y
| Toppunkter | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Derfor er det optimale løsningsmaksimum Z = 1800 ved koordinat x = 0 og y = 450. Grafen er vist nedenfor.

Ajourførte anvendelser af lineær programmering
Lineær programmering, en kraftfuld matematisk teknik, bruges til at løse optimeringsproblemer i forskellige brancher. Her er nogle moderne applikationer:
- Supply Chain Optimering : Lineær programmering hjælper virksomheder med at minimere omkostninger og maksimere effektiviteten i deres forsyningskæder. Det bruges til at bestemme de mest omkostningseffektive transportruter, lagerdrift og lagerstyringsstrategier.
- Energiledelse : I energisektoren anvendes lineær programmering til at optimere blandingen af energiproduktionsmetoder. Dette omfatter balancering af traditionelle energikilder med vedvarende energikilder for at reducere omkostninger og miljøpåvirkning og samtidig imødekomme efterspørgslen.
- Design af telekommunikationsnetværk : Lineær programmering hjælper med at designe effektive telekommunikationsnetværk. Det hjælper med at allokere båndbredde, designe netværkslayouts og optimere datastrømmen for at sikre højhastighedskommunikation til lavere omkostninger.
- Finansiel planlægning : Virksomheder og finansanalytikere bruger lineær programmering til porteføljeoptimering, risikostyring og kapitalbudgettering. Det hjælper med at træffe investeringsbeslutninger, der maksimerer afkastet og samtidig minimerer risikoen.
- Sundhedslogistik : I sundhedsvæsenet anvendes lineær programmering for at optimere allokeringen af ressourcer, såsom hospitalssenge, medicinsk personale og udstyr. Det er afgørende for at forbedre patientbehandlingen, reducere ventetider og administrere omkostningerne effektivt.
- Optimering af fremstillingsprocessen : Lineær programmering bruges til at bestemme de optimale produktionsniveauer for flere produkter inden for en produktionsfacilitet under hensyntagen til begrænsninger som arbejdskraft, materialer og maskintilgængelighed.
- Landbrugsplanlægning : Landmænd og landbrugsplanlæggere bruger lineær programmering til at beslutte afgrødevalg, arealanvendelse og ressourceallokering for at maksimere udbytte og overskud, samtidig med at de sparer ressourcer.
- Planlægning af flyselskabets besætning : Flyselskaber anvender lineær programmering til at planlægge besætninger effektivt, hvilket sikrer, at flyvninger er bemandet i overensstemmelse med reglerne og minimerer driftsomkostningerne.
Disse applikationer demonstrerer alsidigheden og kraften ved lineær programmering til at løse komplekse optimeringsproblemer på tværs af forskellige sektorer, hvilket viser dens relevans i nutidens datadrevne verden.
Lineær programmering i operationsforskning
- Kerneværktøj : Lineær programmering er et grundlæggende værktøj i operationsforskning til optimering af ressourcer.
- Beslutningstagning : Hjælper med at træffe de bedste beslutninger vedrørende ressourceallokering, maksimering af fortjeneste eller minimering af omkostninger.
- Brede applikationer : Bruges inden for forskellige områder såsom logistik, fremstilling, økonomi og sundhedspleje til løsning af komplekse problemer.
- Modellering af virkelige verdensproblemer : Forvandler problemer fra den virkelige verden til matematiske modeller for at finde de mest effektive løsninger.
Enkel metode
- Optimeringsalgoritme : Simplex-metoden er en kraftfuld algoritme, der bruges i lineær programmering til at finde den optimale løsning på lineære uligheder.
- Trin-for-trin tilgang : Den bevæger sig iterativt mod den bedste løsning ved at navigere i kanterne af den mulige region defineret af begrænsninger.
- Effektivitet : Kendt for sin effektivitet i løsning af store lineære programmeringsproblemer.
- Alsidighed : Gælder inden for forskellige domæner som kostplanlægning, netværksflows, produktionsplanlægning og mere, hvilket viser dens alsidighed.
Lineær programmering – ofte stillede spørgsmål
Hvad er lineær programmering?
Lineær programmering er et matematisk koncept, som bruges til at optimere et givet lineært problem, som har en række begrænsninger. Ved at bruge lineær programmering får vi det optimale output af det givne problem
Hvad er problemer med lineær programmering?
Lineære programmeringsproblemer (LPP) er de problemer, der giver den optimale løsning på de givne forhold.
Hvad er lineær programmeringsformel?
Generelle lineære programmeringsformler er,
- Objektiv funktion: Z = axe + by
- Begrænsninger: px + qy ≤ r, sx + ty ≤ u
- Ikke-negative begrænsninger: x ≥ 0, y ≥ 0
Hvad er de forskellige typer lineær programmering?
Forskellige typer af lineære programmeringsmetoder er,
- Lineær programmering ved simplex metode
- Lineær programmering ved R-metoden
- Lineær programmering ved grafisk metode
Hvad er kravene til lineær programmering?
Forskellige krav til lineære programmeringsproblemer er,
- Linearitet
- Objektiv funktion
- Begrænsninger
- Ikke-negativitet
Hvad er fordelene ved lineær programmering?
Forskellige fordele ved lineær programmering er,
- Det giver den optimale løsning på ethvert givet lineært problem.
- Den er nem at bruge og giver altid ensartede resultater
- Det hjælper med at maksimere fortjenesten og reducere inputomkostningerne.