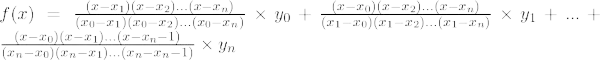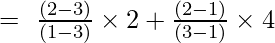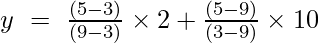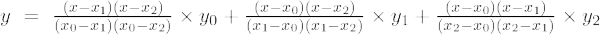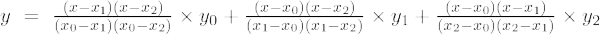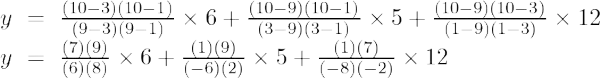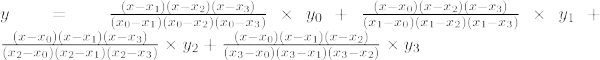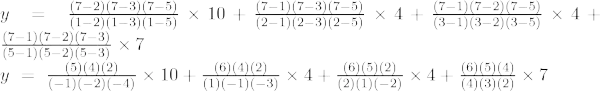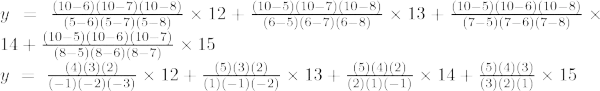logo

TechCodeview

Lagrange interpolationsformel

Lagrange interpolationsformel finder et polynomium kaldet Lagrange Polynomium, der antager bestemte værdier på et vilkårligt punkt. Det er en n. grad polynomisk udtryk for funktionen f(x). Interpolationsmetoden bruges til at finde de nye datapunkter inden for området af et diskret sæt af kendte datapunkter.

I denne artikel vil vi lære om Lagrange Interpolation, Lagrange Interpolation Formula, Proof for Lagrange Interpolation Formula, Eksempler baseret på Lagrange Interpolation Formula og andre i detaljer.



Hvad er Lagrange Interpolation?

Lagrange-interpolation er en måde at finde værdien af ​​en funktion på et givet tidspunkt, når funktionen ikke er givet. Vi bruger andre punkter på funktionen for at få værdien af ​​funktionen på ethvert nødvendigt punkt.

Antag, at vi har en funktion y = f(x), hvor substituering af værdierne af x giver forskellige værdier af y. Og vi får to point (x1, og1) og (x2, og2) på kurven så beregnes værdien af ​​y ved x = a(konstant) ved hjælp af Lagrange Interpolation Formel.

Lagrange interpolationsformel

Givet få reelle værdier x1, x2, x3, …, xnog y1, og2, og3, …, ognog der vil være et polynomium P med reelle koefficienter, der opfylder betingelserne P(xjeg) = ogjeg, ∀ i = {1, 2, 3, …, n} og graden af ​​polynomiet P skal være mindre end antallet af reelle værdier, dvs. grad(P)



Lagrange-interpolationsformel for n. orden

Lagrange-interpolationsformlen for nthgrad polynomium er givet nedenfor:

Lagrange-interpolationsformel for n th rækkefølgen er,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} gange y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} gange y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} gange y_n



Lagrange første ordens interpolationsformel

Hvis Graden af ​​polynomiet er 1, så kaldes det første ordens polynomium. Lagrange interpolationsformel for 1strækkefølgen polynomier er,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} gange y_0+frac{(x-x_0)}{(x_1-x_0)} gange y_1

Lagrange anden ordens interpolationsformel

Hvis graden af ​​polynomiet er 2, kaldes det anden ordens polynomium. Lagrange interpolationsformel for 2. ordens polynomier er,

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} gange y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} gange y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} gange y_2

Bevis for Lagrange-sætningen

Lad os overveje et n. grads polynomium af den givne form,

maskinskriftsdato

f(x) = A0(x – x1)(x – x2)(x – x3)...(x – xn) + A1(x – x1)(x – x2)(x – x3)...(x – xn) + … + A(n-1)(x – x1)(x – x2)(x – x3)...(x – xn)

Erstatningsobservationer xjegat få Ajeg

Sæt x = x0så får vi A0

f(x0) = og0= A0(x0- x1)(x0- x2)(x0- x3)…(x0- xn)

EN 0 = og 0 /(x 0 - x 1 )(x 0 - x 2 )(x 0 - x 3 )…(x 0 - x n )

Ved at erstatte x = x1vi får A1

f(x1) = og1= A1(x1- x0)(x1- x2)(x1- x3)…(x1- xn)

EN 1 = og 1 /(x 1 - x 0 )(x 1 - x 2 )(x 1 - x 3 )…(x 1 - x n )

På samme måde ved at erstatte x = xnvi får An

f(xn) = ogn= An(xn- x0)(xn- x1)(xn- x2)…(xn- xn-1)

EN n = og n /(x n - x 0 )(x n - x 1 )(x n - x 2 )…(x n - x n-1 )

Hvis vi erstatter alle værdier af Ajegi funktion f(x) hvor i = 1, 2, 3, …n får vi Lagrange Interpolation Formel som,

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} gange y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} gange y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} gange y_n

Egenskaber for Lagrange Interpolation Formula

Forskellige egenskaber ved Lagrange-interpolationsformlen diskuteres nedenfor,

  • Denne formel bruges til at finde værdien af ​​funktionen på ethvert tidspunkt, selv når selve funktionen ikke er givet.
  • Det bruges, selvom de angivne punkter ikke er jævnt fordelt.
  • Det giver værdien af ​​den afhængige variabel for enhver uafhængig variabel, der tilhører enhver funktion og bruges således i Numeracial Analysis til at finde værdierne af funktionen osv.

Brug af Lagrange Interpolation Formel

Forskellige anvendelser af Lagrange Interpolation Formel diskuteres nedenfor,

  • Det bruges til at finde værdien af ​​den afhængige variabel ved enhver bestemt uafhængig variabel, selvom selve funktionen ikke er givet.
  • Det bruges til billedskalering.
  • Det bruges i AI-modellering.
  • Det bruges til at undervise i NLP'er osv.

Læs mere,

  • Interpolationsformel
  • Lineær interpolationsformel

Eksempler på brug af lagrange-interpolationsformel

Lad os se på et par prøvespørgsmål om Lagrange Interpolation Formula.

Eksempel 1: Find værdien af ​​y ved x = 2 for det givne sæt af punkter (1, 2), (3, 4)

Løsning:

givet,

  • (x0, og0) = (1, 2)
  • (x1, og1) = (3, 4)

Første ordens Lagrange Interpolation Formel er,

y~=~frac{(x-x_1)}{(x_0-x_1)} gange y_0+frac{(x-x_0)}{(x_1-x_0)} gange y_1

Ved x = 2

og =~frac{(2-3)}{(1-3)} gange 2+frac{(2-1)}{(3-1)} gange 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Værdien af ​​y ved x = 2 er 3

Eksempel 2: Find værdien af ​​y ved x = 5 for det givne sæt af punkter (9, 2), (3, 10)

Løsning:

givet,

  • (x0, og0) = (9, 2)
  • (x1, og1) = (3, 10)

Første ordens Lagrange Interpolation Formel er,

y~=~frac{(x-x_1)}{(x_0-x_1)} gange y_0+frac{(x-x_0)}{(x_1-x_0)} gange y_1

Ved x = 5

y~=~frac{(5-3)}{(9-3)} gange 2+frac{(5-9)}{(3-9)} gange 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Værdien af ​​y ved x = 5 er 7,33

Eksempel 3: Find værdien af ​​y ved x = 1 for det givne sæt af punkter (1, 6), (3, 4), (2, 5)

Løsning:

givet,

  • (x0, og0) = (1, 6)
  • (x1, og1) = (3, 4)
  • (x2, og2) = (2, 5)

Anden ordens lagrange interpolationsformel er,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} gange y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} gange y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} gange y_2

Ved x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} gange 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} gange 4+frac{(1-1)(1-3)}{(2-1)(2-3)} gange 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} gange 6+frac{(0)(-1)}{(2)(1)} gange 4+frac {(0)(-2)}{(1)(-1)} gange 5

y = (12/2) + 0 + 0

y = 6

Værdien af ​​y ved x = 1 er 6

Eksempel 4: Find værdien af ​​y ved x = 10 for det givne sæt af punkter (9, 6), (3, 5), (1, 12)

Løsning:

givet,

  • (x0, og0) = (9, 6)
  • (x1, og1) = (3, 5)
  • (x2, og2) = (1, 12)

Anden ordens lagrange interpolationsformel er,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} gange y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} gange y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} gange y_2

Ved x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} gange 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} gange 5+frac{(10-9)(10-3)}{(1-9)(1-3)} gange 12 y~=~ frac{(7)(9)}{(6)(8)} gange 6+frac{(1)(9)}{(-6)(2)} gange 5+frac{(1) (7)}{(-8)(-2)} gange 12

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Værdien af ​​y ved x = 10 er 9,375

Eksempel 5: Find værdien af ​​y ved x = 7 for det givne sæt af punkter (1, 10), (2, 4), (3, 4), (5, 7)

Løsning:

givet,

  • (x0, og0) = (1, 10)
  • (x1, og1) = (2, 4)
  • (x2, og2) = (3, 4)
  • (x3, og3) = (5, 7)

Tredje ordens lagrange interpolationsformel er,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} gange y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} gange y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} gange y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)} gange y_3

Ved x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} gange 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} gange 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} gange 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} gange 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} gange 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} gange 4+frac{(6)(5)(2)}{(2)(1) (-2)} gange 4+frac{(6)(5)(4)}{(4)(3)(2)} gange 7

y = -50 + 64 – 60 + 35

y = 99 – 110 = -elleve

Værdien af ​​y ved x = 7 er -11

Eksempel 6: Find værdien af ​​y ved x = 10 for det givne sæt af punkter (5, 12), (6, 13), (7, 14), (8, 15)

Løsning:

givet,

  • (x0, og0) = (5, 12)
  • (x1, og1) = (6, 13)
  • (x2, og2) = (7, 14)
  • (x3, og3) = (8, 15)

Tredje ordens lagrange interpolationsformel er,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} gange y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} gange y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} gange y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)} gange y_3

Ved x = 10,

matematik tilfældig java

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} gange 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} gange 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} gange 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} gange 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} gange 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} gange 13+frac{(5)(4)(2)}{(2)(1) (-1)} gange 14+frac{(5)(4)(3)}{(3)(2)(1)} gange 15

y = -48 + 195 – 280 + 150

y = 17

Værdien af ​​y ved x = 10 er 17

Eksempel 7: Find værdien af ​​y ved x = 0 for det givne sæt af punkter (-2, 5),(1, 7)

Løsning:

givet,

  • (x0, og0) = (-2, 5)
  • (x1, og1) = (1, 7)

First Order Lagrange Interpolation Formel er,

y~=~frac{(x-x_1)}{(x_0-x_1)} gange y_0+frac{(x-x_0)}{(x_1-x_0)} gange y_1

Ved x = 0,

y~=~frac{(0-1)}{(-2-1)} gange 5+frac{(0+2)}{(1+2)} gange 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Værdien af ​​y ved x = 0 er 6,33

Ofte stillede spørgsmål om Lagrange Interpolation Formula

1. Hvad er Lagrange Interpolation Formel?

Lagrange Interpolation Formel er en formel, der bruges til at finde værdien af ​​funktionens afhængige variabel for enhver uafhængig variabel, selvom selve funktionen ikke er givet.

2. Hvad er anvendelserne af Lagrange Interpolation Formel?

Lagranges Formula har forskellige anvendelser i moderne matematik og datavidenskab,

  • Det bruges til AI-modellen Traning.
  • Det bruges i billedbehandling.
  • Det bruges til at tegne 3-D og højere kurver osv.

3. Hvad er First Order Lagrange Interpolation Formula?

First Order Lagranges Interpolation Formel er,

f(x) = (x – x 1 )/(x 0 - x 1 )×f 0 + (x – x 0 )/(x 1 - x 0 )×f 1

4. Hvad er Second Order Lagrange Interpolation Formel?

Anden ordens lagranges interpolationsformel er,

f(x) = [(x – x 1 )(x – x 2 )/(x 0 - x 1 )(x 0 - x 2 )]×f 0 + [(x – x 0 )(x – x 2 )/(x 1 - x 0 )(x 1 - x 2 )]×f 1 + [(x – x 0 )(x – x 1 )/(x 2 - x 0 )(x 2 - x 2 )]×f 0