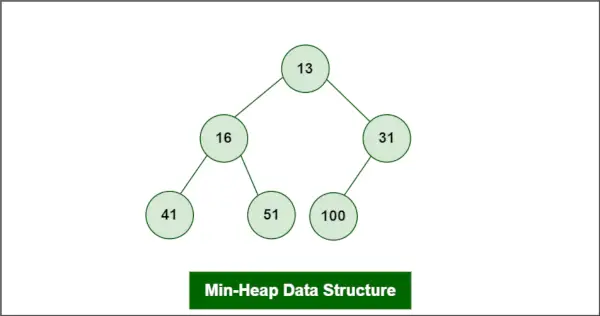
EN Min-Heap er defineret som en type Heap-datastrukturen er en type binært træ, der almindeligvis bruges i datalogi til forskellige formål, herunder sortering, søgning og organisering af data.
Introduktion til Min-Heap – Datastruktur og algoritmevejledninger
Formål og anvendelsestilfælde af Min-Heap:
- Implementering af prioritetskø: En af de primære anvendelser af heap-datastrukturen er til implementering af prioritetskøer.
- Dijkstras algoritme : Dijkstras algoritme er en korteste vejs algoritme, der finder den korteste vej mellem to noder i en graf. En min heap kan bruges til at holde styr på de ubesøgte noder med den mindste afstand fra kildenoden.
- Sortering: En min heap kan bruges som en sorteringsalgoritme til effektivt at sortere en samling af elementer i stigende rækkefølge.
- Median fund: En min heap kan bruges til effektivt at finde medianen af en strøm af tal. Vi kan bruge en min bunke til at gemme den største halvdel af tallene og en max bunke til at gemme den mindre halvdel. Medianen vil være roden af min-heapen.
Min-Heap-datastruktur på forskellige sprog:
1. Min-Heap i C++
En min heap kan implementeres ved hjælp af priority_queue container fra Standard Template Library (STL). Det priority_queue container er en type containeradapter, der giver en måde at gemme elementer i en kølignende datastruktur, hvor hvert element har en prioritet knyttet til sig.
Syntaks :
C++ priority_queue < int, vector , større > minH;>
2. Min-Heap i Java
I Java kan en min heap implementeres ved hjælp af Prioritetskø klasse fra java.util-pakken . PriorityQueue-klassen er en prioritetskø, der giver en måde at gemme elementer i en kølignende datastruktur, hvor hvert element har en prioritet tilknyttet.
Syntaks :
Java PriorityQueue minHeap = ny PriorityQueue ();>
3. Min-Heap i Python
I Python kan en min heap implementeres ved hjælp af heapq modul, som giver funktioner til implementering af heaps. Specifikt heapq modul giver en måde at skabe og manipulere heap-datastrukturer på.
Syntaks:
Python heap = [] heapify(heap)>
4. Min-Heap i C#
I C# kan en min heap implementeres ved hjælp af PriorityQueue-klassen fra System.Collections.Generisk navneområde . PriorityQueue-klassen er en prioritetskø, der giver en måde at gemme elementer i en kølignende datastruktur, hvor hvert element har en prioritet tilknyttet.
Syntaks:
C# var minHeap = new PriorityQueue ();>
5. Min-heap i JavaScript
En min heap er et binært træ, hvor hver node har en værdi mindre end eller lig med dens børn. I JavaScript kan du implementere en min heap ved hjælp af et array, hvor det første element repræsenterer rodnoden og børnene af en knude ved indeks jeg er placeret ved indekser 2i+1 og 2i+2.
Syntaks:
JavaScript const minHeap = new MinHeap();>
Forskellen mellem Min Heap og Max Heap:
|
| Min bunke | Max Heap |
|---|---|---|
| 1. | I en Min-Heap skal nøglen, der er til stede ved rodnoden, være mindre end eller lig med blandt nøglerne, der er til stede ved alle dens børn. | I en Max-Heap skal nøglen, der er til stede ved rodnoden, være større end eller lig med blandt nøglerne, der er til stede ved alle dens børn. |
| 2. | I en Min-Heap er minimumsnøgleelementet til stede ved roden. | I en Max-Heap er det maksimale nøgleelement til stede ved roden. |
| 3. | En Min-Heap bruger den stigende prioritet. | En Max-Heap bruger den faldende prioritet. |
| 4. | I konstruktionen af en Min-Heap har det mindste element prioritet. | Ved konstruktionen af en Max-Heap har det største element prioritet. |
| 5. | I en Min-Heap er det mindste element det første, der bliver poppet fra dyngen. forskel mellem array og arraylist | I en Max-Heap er det største element det første, der bliver poppet fra dyngen. |
Intern implementering af Min-Heap-datastruktur:
EN Min heap er typisk repræsenteret som en matrix .
- Rodelementet vil være kl Arr[0] .
- For enhver it-node Arr[i] :
- Arr[(i -1) / 2] returnerer sin overordnede node.
- Arr[(2 * i) + 1] returnerer sin venstre underordnede node.
- Arr[(2 * i) + 2] returnerer sin højre underordnede node.
Den interne implementering af min-heapen kræver 3 store trin:
- Indskud : For at indsætte et element i min-heapen, tilføjer vi først elementet til enden af arrayet og justerer derefter heap-egenskaben ved gentagne gange at bytte elementet med dets overordnede, indtil det er i den korrekte position.
- Sletning : For at fjerne minimumselementet fra min-heapen, bytter vi først rodnoden med det sidste element i arrayet, fjerner det sidste element og justerer derefter heap-egenskaben ved gentagne gange at bytte elementet med dets mindste underordnede, indtil det er i korrekt position.
- Heapify : En heapify-operation kan bruges til at oprette en min heap fra et usorteret array.
Operationer på min-heap datastruktur og deres implementering:
Her er nogle almindelige operationer, der kan udføres på en heap-datastruktur,
1. Indsættelse i Min-Heap-datastruktur :
Elementer kan indsættes i heapen efter en lignende fremgangsmåde som diskuteret ovenfor til sletning. Ideen er at:
- Indsættelsesoperationen i en min-heap involverer følgende trin:
- Tilføj det nye element til enden af bunken, i den næste tilgængelige position i træets sidste niveau.
- Sammenlign det nye element med dets overordnede element. Hvis forælderen er større end det nye element, skal du bytte dem.
- Gentag trin 2, indtil forælderen er mindre end eller lig med det nye element, eller indtil det nye element når roden af træet.
- Det nye element er nu i sin korrekte position i min-heapen, og heap-egenskaben er opfyldt.
Illustration:
Antag, at Heapen er en Min-Heap som:
Indsættelse i Min-Heap
Implementering af indsættelsesoperation i Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int værdi) { // Tilføj det nye element til slutningen af heapen heap.push_back(value); // Hent indekset for det sidste element int index = heap.size() - 1; // Sammenlign det nye element med dets overordnede element og swap, hvis // er nødvendigt while (indeks> 0 && heap[(indeks - 1) / 2]> heap[indeks]) { swap(heap[indeks], heap[(indeks - 1) / 2]); // Flyt op i træet til forælderen af det aktuelle // element index = (indeks - 1) / 2; } } // Hovedfunktion til at teste funktionen insert_min_heap int main() { vektor bunke; int-værdier[] = { 10, 7, 11, 5, 4, 13 }; int n = størrelse på(værdier) / størrelse på(værdier[0]); for (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && heap[(indeks - 1) / 2]> heap[indeks]) { swap(heap, indeks, (indeks - 1) / 2); // Flyt op i træet til forælderen af det aktuelle // element index = (indeks - 1) / 2; } } // Funktion til at bytte to elementer i et array public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } // Hovedfunktion til at teste insertMinHeap-funktionen public static void main(String[] args) { int[] heap = new int[6]; int[] værdier = { 10, 7, 11, 5, 4, 13 }; int størrelse = 0; for (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 og heap[(indeks - 1) // 2]> heap[indeks]: heap[indeks], heap[(indeks - 1) // 2] = heap[(indeks - 1) // 2], heap[ indeks] # Flyt op i træet til forælderen af det aktuelle element indeks = (indeks - 1) // 2 heap = [] værdier = [10, 7, 11, 5, 4, 13] for værdi i værdier: insert_min_heap( heap, value) print(f'Indsat {value} i min-heapen: {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List heap, int value) { // Tilføj det nye element til slutningen af heapen.Add(value); // Få indekset for det sidste element int index = heap.Count - 1; // Sammenlign det nye element med dets overordnede element og skift // om nødvendigt while (indeks> 0 && heap[(indeks - 1) / 2]> heap[indeks]) { int temp = heap[indeks]; heap[indeks] = heap[(indeks - 1) / 2]; heap[(indeks - 1) / 2] = temp; // Flyt op i træet til forælderen af det aktuelle // element index = (indeks - 1) / 2; } } // Hovedfunktion til at teste InsertMinHeap-funktionen public static void Main() { List heap = ny Liste (); int[] værdier = { 10, 7, 11, 5, 4, 13 }; foreach(int værdi i værdier) { InsertMinHeap(heap, værdi); Console.Write('Indsat ' + værdi + ' i min-heapen: '); foreach(int element i heap) { Console.Write(element + ' '); } Console.WriteLine(); } } }> Javascript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && heap[parentIndex]> heap[indeks]) { [heap[indeks], heap[parentIndex]] = [heap[parentIndex], heap[indeks]]; index = parentIndex; parentIndex = Math.floor((indeks - 1) / 2); } } // Eksempel på brug const heap = []; const værdier = [10, 7, 11, 5, 4, 13]; for (konst værdi af værdier) { insertMinHeap(heap, værdi); console.log(`Indsatte ${value} i min-heapen: ${heap}`); }> Produktion
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Tidskompleksitet: O(log(n)) ( hvor n er antallet af elementer i bunken )
Hjælpeplads: På)
2. Sletning i Min-Heap-datastruktur :
Fjernelse af det mindste element (roden) fra min-bunken. Roden erstattes af det sidste element i heapen, og derefter genoprettes heap-egenskaben ved at bytte den nye rod med dens mindste underordnede, indtil forælderen er mindre end begge børn, eller indtil den nye rod når en bladknude.
- Erstat roden eller elementet, der skal slettes, med det sidste element.
- Slet det sidste element fra heapen.
- Da det sidste element nu er placeret ved positionen af rodknuden. Så den følger muligvis ikke bunkeejendommen. Derfor skal du ophobe den sidste node placeret ved rodens position.
Illustration :
Antag, at Heapen er en Min-Heap som:
Min-Heap-datastruktur
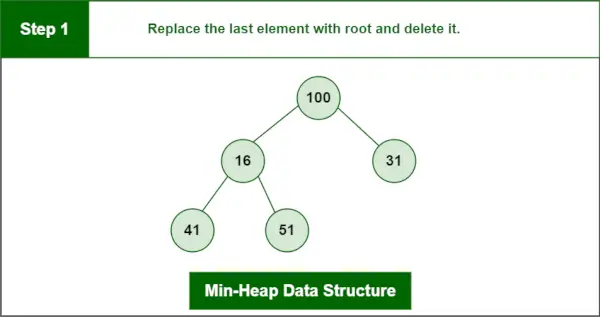
Elementet, der skal slettes, er root, dvs. 13.
Behandle :
Det sidste element er 100.
Trin 1: Erstat det sidste element med root, og slet det.
Min-Heap-datastruktur
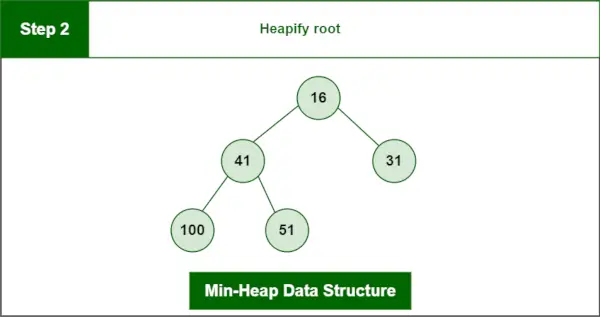
Trin 2 : Ophob rod.
Sidste bunke:
Min-Heap-datastruktur
Implementering af sletningsoperation i Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int værdi) { // Tilføj det nye element til slutningen af heapen heap.push_back(value); // Hent indekset for det sidste element int index = heap.size() - 1; // Sammenlign det nye element med dets overordnede element og swap, hvis // er nødvendigt while (indeks> 0 && heap[(indeks - 1) / 2]> heap[indeks]) { swap(heap[indeks], heap[(indeks - 1) / 2]); // Flyt op i træet til forælderen af det aktuelle // element index = (indeks - 1) / 2; } } // Funktion til at slette en node fra min-heap void delete_min_heap(vektor & heap, int værdi) { // Find indekset for det element, der skal slettes int index = -1; for (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector bunke; int-værdier[] = { 13, 16, 31, 41, 51, 100 }; int n = størrelse på(værdier) / størrelse på(værdier[0]); for (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List heap, int value) { // Tilføj det nye element til slutningen af heapen heap.add(value); // Hent indekset for det sidste element int index = heap.size() - 1; // Sammenlign det nye element med dets overordnede element og skift // om nødvendigt while (indeks> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (indeks - 1) / 2); // Flyt op i træet til forælderen af det aktuelle // element index = (indeks - 1) / 2; } } // Funktion til at slette en node fra min-heap offentlige statiske void deleteMinHeap(List heap, int værdi) { // Find indekset for det element, der skal slettes int index = -1; for (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List heap = ny ArrayList (); int[] værdier = { 13, 16, 31, 41, 51, 100 }; int n = værdier.længde; for (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 og heap[(indeks - 1) // 2]> heap[indeks]: heap[indeks], heap[(indeks - 1) // 2] = heap[(indeks - 1) // 2], heap[ index] index = (indeks - 1) // 2 def delete_min_heap(heap, værdi): index = -1 for i i området(len(heap)): if heap[i] == værdi: indeks = i break if index == -1: returner heap[indeks] = heap[-1] heap.pop() mens True: left_child = 2 * indeks + 1 right_child = 2 * indeks + 2 mindste = indeks hvis left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List heap = ny Liste (); public void Insert(int value) { heap.Add(value); int index = heap.Count - 1; while (indeks> 0 && heap[(indeks - 1) / 2]> heap[indeks]) { Swap(indeks, (indeks - 1) / 2); indeks = (indeks - 1) / 2; } } public void Delete(int value) { int index = heap.IndexOf(value); if (indeks == -1) { return; } heap[indeks] = heap[heap.Count - 1]; heap.RemoveAt(heap.Count - 1); while (sand) { int leftChild = 2 * indeks + 1; int rightChild = 2 * indeks + 2; int mindste = indeks; hvis (venstreBarn< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && bunke[flr]> bunke[indeks]; flr = Math.floor((indeks - 1) / 2)) { [heap[indeks], heap[flr]] = [heap[flr], heap[indeks], ]; // Flyt op i træet til forælderen af det aktuelle elementindeks = Math.floor((indeks - 1) / 2); } } function deleteMinHeap(heap, value) { // Find indekset for det element, der skal slettes lad index = -1; for (lad i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Produktion
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Tidskompleksitet : O(log n) hvor n er antallet af elementer i heapen
Hjælpeplads: På)
3. Peek-operation på Min-Heap-datastruktur:
For at få adgang til minimumselementet (dvs. roden af heapen), returneres værdien af rodknuden. Tidskompleksiteten af kig i en min-heap er O(1).
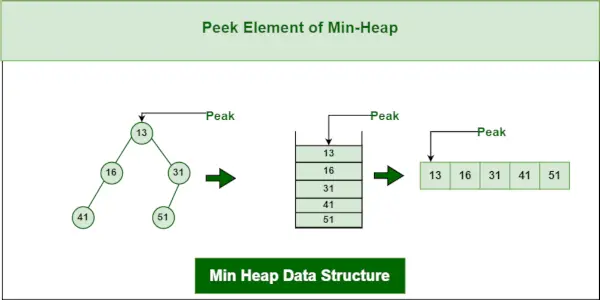
Min heap datastruktur
Implementering af Peek-operation i Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , større > minHeap; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Få peak-elementet (dvs. det største element) int peakElement = minHeap.top(); // Udskriv peak element cout<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = new PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Få peak-elementet (dvs. det største element) int peakElement = minHeap.peek(); // Udskriv peak elementet System.out.println('Peak element: ' + peakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Få peak-elementet (dvs. det mindste element) int peakElement = minHeap.Peek(); // Udskriv peak elementet Console.WriteLine('Peak element: ' + peakElement); } }> Javascript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Hent peak-elementet (dvs. det mindste element) const peakElement = minHeap.peek(); // Udskriv peak-elementet console.log(`Peak element: ${peakElement}`);> Produktion
Peak element: 1>
Tidskompleksitet : I en min-heap implementeret ved hjælp af et array eller en liste, kan peak-elementet tilgås i konstant tid, O(1), da det altid er placeret ved roden af heapen.
I en min heap implementeret ved hjælp af et binært træ, kan peak-elementet også tilgås i O(1) tid, da det altid er placeret ved roden af træet.
Hjælpeplads: På)
4. Heapify-operation på Min-Heap-datastruktur:
En heapify-operation kan bruges til at oprette en min heap fra et usorteret array. Dette gøres ved at starte ved den sidste ikke-bladsknude og gentagne gange udføre boble ned-operationen, indtil alle noder opfylder heap-egenskaben.
Heapify-operation i Min Heap
Implementering af Heapify-operation i Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int mindste = i; int l = 2*i + 1; int r = 2*i + 2; hvis (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Antag, at roden er det mindste element oprindeligt int mindste = i; // Beregn indekserne for venstre og højre underordnede af den aktuelle node int l = 2 * i + 1; int r = 2 * i + 2; // Sammenlign det venstre barn med det nuværende mindste, hvis (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Original array: '); // Udskriv det originale array for (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Heap efter heapify-operation: '); // Udskriv min-heapen efter heapify-operation for (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int mindste = i; int venstre = 2 * i + 1; int højre = 2 * i + 2; // Sammenlign det venstre barn med den aktuelle mindste node. hvis (venstre< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = ny liste { 10, 5, 15, 2, 20, 30 }; Console.Write('Original array: '); foreach (int num i arr) Console.Write(num + ' '); // Udfør heapify-operation på min-heapen. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap efter heapify-operation: '); foreach (int num i arr) Console.Write(num + ' '); } }> Javascript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.længde); // Udskriv min-heap efter heapify operation console.log('Min-Heap efter heapify operation: ' + arr.join(' ')); } // Kald hovedfunktionen for at starte processen main();> Produktion
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
Tidskompleksiteten af heapify i en min-heap er O(n).
5. Søgeoperation på Min-Heap Data Structure:
For at søge efter et element i min-heapen kan der udføres en lineær søgning over det array, der repræsenterer heapen. Imidlertid er tidskompleksiteten af en lineær søgning O(n), hvilket ikke er effektivt. Derfor er søgning ikke en almindeligt brugt operation i en min heap.
Her er et eksempel på en kode, der viser, hvordan man søger efter et element i en min bunke ved hjælp af std::find() :
C++ #include using namespace std; int main() { priority_queue , større > min_heap; // eksempel max heap min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int element = 6; // element til at søge efter bool fundet = false; // Kopier min heap til en midlertidig kø og søg efter // elementet std::priority_queue , større > temp = min_heap; while (!temp.empty()) { if (temp.top() == element) { found = true; pause; } temp.pop(); } if (fundet) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = ny PriorityQueue(); min_heap.add( 3); // indsæt elementer i prioritetskøen min_heap.offer(1); min_heap.offer(4); min_heap.offer(1); min_heap.offer(6); int element = 6; // element til at søge efter boolesk fundet = falsk; // Kopier min-bunken til en midlertidig kø og søg // efter elementet PriorityQueue temp = new PriorityQueue(min_heap); while (!temp.isEmpty()) { if (temp.poll() == element) { found = true; pause; } } if (fundet) { System.out.println( 'Element fundet i min heap.'); } else { System.out.println( 'Element ikke fundet i min-heapen.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // eksempel min heap minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); int element = 6; // element til at søge efter bool fundet = false; // Kopier min-bunken til en midlertidig kø og søg // efter elementet var temp = new PriorityQueue (minHeap); while (temp.Count> 0) { if (temp.Peek() == element) { found = true; pause; } temp.Dequeue(); } if (fundet) { Console.WriteLine( 'Element fundet i min-bunken.'); } else { Console.WriteLine( 'Element ikke fundet i min-bunken.'); } } }> Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == element) { fundet = sand; pause; } temp.dequeue(); } if (fundet) { console.log('Element fundet i min heap.'); } else { console.log('Element ikke fundet i min heap.'); }> Produktion
Element found in the min heap.>
Kompleksitetsanalyse :
Det tidskompleksitet af dette program er O(n log n) , hvor n er antallet af elementer i prioritetskøen.
Indsættelsesoperationen har en tidskompleksitet på O(log n) i værste fald fordi dyngeejendommen skal vedligeholdes. Søgeoperationen involverer at kopiere prioritetskøen til en midlertidig kø og derefter krydse den midlertidige kø, hvilket tager O(n log n) tid i værste fald, fordi hvert element skal kopieres og poppes fra køen, og prioritetskøen skal genopbygges for hver operation.
Det rummets kompleksitet af programmet er På) fordi den gemmer n elementer i prioritetskøen og opretter en midlertidig kø med n elementer.
Anvendelser af min-heap datastruktur:
- Hobe sortering: Min heap bruges som en nøglekomponent i heap-sorteringsalgoritme, som er en effektiv sorteringsalgoritme med en tidskompleksitet på O(nlogn).
- Prioritetskø: En prioritetskø kan implementeres ved hjælp af en min heap-datastruktur, hvor elementet med minimumsværdien altid er ved roden.
- Dijkstras algoritme: I Dijkstras algoritme bruges en min heap til at lagre grafens toppunkter med minimumsafstanden fra startpunktet. Toppunktet med den mindste afstand er altid ved roden af bunken.
- Huffman kodning: I Huffman-kodning bruges en min heap til at implementere en prioritetskø for at bygge en optimal præfikskode for et givet sæt tegn.
- Flet K sorterede arrays: Givet K sorterede arrays, kan vi flette dem til et enkelt sorteret array effektivt ved hjælp af en min heap datastruktur.
Fordele ved min-heap datastruktur:
- Effektiv indsættelse og sletning : Min heap tillader hurtig indsættelse og sletning af elementer med en tidskompleksitet på O(log n), hvor n er antallet af elementer i heapen.
- Effektiv hentning af minimumselement: Minimumselementet i en min heap er altid ved roden af heapen, som kan hentes i O(1) tid.
- Pladseffektiv: Min heap er en kompakt datastruktur, der kan implementeres ved hjælp af et array eller et binært træ, hvilket gør det pladseffektivt.
- Sortering: Min heap kan bruges til at implementere en effektiv sorteringsalgoritme såsom heap sortering med en tidskompleksitet på O(n log n).
- Prioritetskø: Min heap kan bruges til at implementere en prioritetskø, hvor elementet med minimum prioritet kan hentes effektivt på O(1) tid.
- Alsidighed: Min heap har flere applikationer inden for datalogi, herunder grafalgoritmer, datakomprimering og databasesystemer.
Samlet set er min heap en nyttig og alsidig datastruktur, der tilbyder effektiv drift, pladseffektivitet og har adskillige applikationer inden for datalogi.
hvordan man konverterer en streng til en int