Finite Automata(FA) er den enkleste maskine til at genkende mønstre. Den bruges til at karakterisere et almindeligt sprog, for eksempel: /baa+!/.
Det bruges også til at analysere og genkende naturlige sprogudtryk. Finite automata eller finite state machine er en abstrakt maskine, der har fem elementer eller tupler. Det har et sæt tilstande og regler for at flytte fra en tilstand til en anden, men det afhænger af det anvendte inputsymbol. Baseret på tilstandene og regelsættet kan inputstrengen enten accepteres eller afvises. Grundlæggende er det en abstrakt model af en digital computer, som læser en inputstreng og ændrer dens interne tilstand afhængigt af det aktuelle inputsymbol. Hver automat definerer et sprog, dvs. sæt strenge, den accepterer. Den følgende figur viser nogle væsentlige funktioner i generel automatisering.
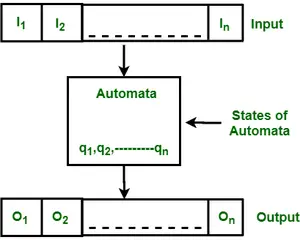
Figur: Funktioner af Finite Automata
Ovenstående figur viser følgende funktioner i automater:
sorteret arraylist i java
- Input
- Produktion
- Automater
- Statsforhold
- Output forhold
En endelig automat består af følgende:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Formel specifikation af maskine er
{ Q, ?, q, F, ? }> FA er karakteriseret i to typer:
1) Deterministic Finite Automata (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->Q.> I en DFA går maskinen kun til én tilstand for et bestemt inputtegn. En overgangsfunktion er defineret for hver tilstand for hvert inputsymbol. Også i DFA er null (eller ?) flytning ikke tilladt, dvs. DFA kan ikke ændre tilstand uden noget inputtegn.
streng format java
Konstruer for eksempel en DFA, som accepterer et sprog med alle strenge, der ender med 'a'.
Givet: ? = {a,b}, q = {q0}, F={q1}, Q = {q0, q1}
Overvej først et sprogsæt af alle de mulige acceptable strenge for at konstruere et nøjagtigt tilstandsovergangsdiagram.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, far, far, far, far}
Ovenfor er en simpel delmængde af de mulige acceptable strenge, der kan mange andre strenge, som slutter med 'a' og indeholder symboler {a,b}.
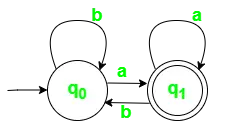
Fig 1. Tilstandsovergangsdiagram for DFA med ? = {a, b}
Strenge, der ikke accepteres, er,
ab, bb, aab, abbb osv.
Tilstandsovergangstabel for ovenstående automat,
| ?StatSymbol? | -en | b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q0 |
En vigtig ting at bemærke er, der kan være mange mulige DFA'er for et mønster . En DFA med et minimum antal stater foretrækkes generelt.
2) Nondeterministic Finite Automata (NFA): NFA ligner DFA bortset fra følgende yderligere funktioner:
- Nul (eller ?) bevægelse er tilladt, dvs. den kan bevæge sig fremad uden at læse symboler.
- Evne til at transmittere til et vilkårligt antal tilstande for et bestemt input.
Disse ovenstående funktioner tilføjer dog ingen strøm til NFA. Hvis vi sammenligner begge med hensyn til magt, er begge ækvivalente.
junit test cases
På grund af ovenstående ekstra funktioner har NFA en anden overgangsfunktion, resten er den samme som DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Q.>
Som du kan se i overgangsfunktionen er for enhver input inklusive null (eller ?), kan NFA gå til et hvilket som helst antal stater. For eksempel er nedenfor en NFA for ovenstående problem.
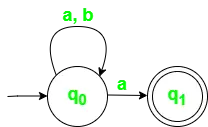
Fig 2. Tilstandsovergangsdiagram for NFA med ? = {a, b}
Tilstandsovergangstabel for ovenstående automat,
netværk og netværkstyper
| ?StatSymbol? | -en | b |
|---|---|---|
| q0 | {q0,q1} | q0 |
| q1 | ? | ? |
En vigtig ting at bemærke er, i NFA, hvis en sti for en inputstreng fører til en endelig tilstand, så inputstrengen er accepteret . For eksempel er der i ovenstående NFA flere stier til inputstrengen 00. Da en af stierne fører til en endelig tilstand, accepteres 00 af ovenstående NFA.
Nogle vigtige punkter:
- Begrundelse:
In case of DFA ? : Q X ? -->Q I tilfælde af NFA? : Q X ? --> 2Q>
Hvis du nu observerer, vil du finde ud af Q X? –> Q er en del af Q X ? –> 2Q.
På RHS-siden er Q delmængden af 2Qhvilket indikerer, at Q er indeholdt i 2Qeller Q er en del af 2Qdet omvendte er dog ikke sandt. Så matematisk kan vi konkludere det hver DFA er NFA, men ikke omvendt . Alligevel er der en måde at konvertere en NFA til DFA, så der findes en tilsvarende DFA for hver NFA .
- Både NFA og DFA har samme magt, og hver NFA kan oversættes til en DFA.
- Der kan være flere sluttilstande i både DFA og NFA.
- NFA er mere et teoretisk begreb.
- DFA bruges i leksikalsk analyse i compiler.
- Hvis antallet af stater i NFA er N, kan dens DFA maksimalt have 2Nantal stater.
Se Quiz om regulært udtryk og endelige automater.
