Den algoritmiske verden er smuk med mangfoldige strategier og værktøjer, der udvikles døgnet rundt for at imødekomme behovet for højtydende databehandling. Faktisk, når algoritmer er inspireret af naturlove, observeres interessante resultater. Evolutionære algoritmer tilhører en sådan klasse af algoritmer. Disse algoritmer er designet til at efterligne visse adfærd såvel som evolutionære træk ved det menneskelige genom. Desuden er et sådant algoritmisk design ikke kun begrænset til mennesker, men kan også være inspireret af visse dyrs naturlige adfærd. Det grundlæggende formål med at fremstille sådanne metoder er at give realistiske, relevante og alligevel nogle billige løsninger på problemer, der hidtil er uløselige med konventionelle midler.
Forskellige optimeringsteknikker har således udviklet sig baseret på sådanne evolutionære algoritmer og derved åbnet op for metaheuristikkens domæne. Metaheuristisk er afledt af to græske ord, nemlig Meta betyder et niveau over og heuriskein betyder at finde . Algoritmer som partikelsværmoptimering (PSO) og myrekolonioptimering (ACO) er eksempler på sværm-intelligens og metaheuristik. Målet med sværm intelligens er at designe intelligente multi-agent systemer ved at tage inspiration fra den kollektive adfærd af sociale insekter såsom myrer, termitter, bier, hvepse og andre dyresamfund såsom flokke af fugle eller fiskestimer.
Baggrund:
1 milliard til mio
Ant Colony Optimization-teknikken er udelukkende inspireret af fouragering opførsel af myrekolonier, først introduceret af Marco Dorigo i 1990'erne. Myrer er eusociale insekter, der foretrækker samfundets overlevelse og opretholdelse frem for som individuelle arter. De kommunikerer med hinanden ved hjælp af lyd, berøring og feromon. Feromoner er organiske kemiske forbindelser udskilt af myrerne, der udløser en social reaktion hos medlemmer af samme art. Disse er kemikalier, der er i stand til at virke som hormoner uden for kroppen af det udskillende individ, for at påvirke de modtagende individers adfærd. Da de fleste myrer lever på jorden, bruger de jordoverfladen til at efterlade feromonspor, som kan følges (lugtes) af andre myrer.
Myrer lever i samfundsreder, og det underliggende princip for ACO er at observere myrernes bevægelse fra deres reder for at søge efter føde på kortest mulig vej. Til at begynde med begynder myrer at bevæge sig tilfældigt på jagt efter føde omkring deres reder. Denne randomiserede søgning åbner op for flere ruter fra reden til fødekilden. Nu, baseret på kvaliteten og mængden af maden, bærer myrer en del af maden tilbage med nødvendig feromonkoncentration på dens returvej. Afhængigt af disse feromonforsøg vil sandsynligheden for valg af en specifik vej af følgende myrer være en vejledende faktor for fødekilden. Denne sandsynlighed er åbenbart baseret på koncentrationen såvel som hastigheden af fordampning af feromon. Det kan også observeres, at da fordampningshastigheden af feromon også er en afgørende faktor, kan længden af hver vej nemt tages i betragtning.
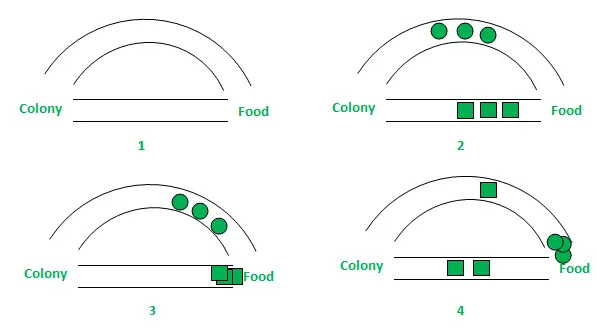
I ovenstående figur er der for nemheds skyld kun overvejet to mulige veje mellem fødekilden og myreredet. Faserne kan analyseres som følger:
række af array i c
- Trin 1: Alle myrer er i deres rede. Der er intet feromonindhold i miljøet. (For algoritmisk design kan resterende feromonmængde overvejes uden at forstyrre sandsynligheden) Trin 2: Myrer begynder deres søgning med lige stor (0,5 hver) sandsynlighed langs hver vej. Det er klart, at den buede vej er længere, og derfor er den tid, det tager for myrer at nå fødekilden, længere end den anden. Trin 3: Myrerne gennem den kortere vej når fødekilden tidligere. Nu står de åbenbart over for et lignende udvælgelsesdilemma, men denne gang på grund af feromonsporet langs den kortere vej, der allerede er tilgængelig, er sandsynligheden for udvælgelse højere. Trin 4: Flere myrer vender tilbage via den kortere vej og efterfølgende stiger feromonkoncentrationerne også. Desuden, på grund af fordampning, reduceres feromonkoncentrationen i den længere vej, hvilket mindsker sandsynligheden for valg af denne vej i yderligere trin. Derfor bruger hele kolonien gradvist den kortere vej med højere sandsynlighed. Så stioptimering er opnået.
Algoritmisk design:
Med hensyn til myrernes ovenstående adfærd kan der nu udvikles et algoritmisk design. For nemheds skyld er en enkelt fødekilde og en enkelt myrekoloni blevet overvejet med kun to mulige krydsningsveje. Hele scenariet kan realiseres gennem vægtede grafer, hvor myrekolonien og fødekilden fungerer som knudepunkter (eller knudepunkter); stierne tjener som kanterne, og feromonværdierne er vægtene forbundet med kanterne.
Lad grafen være G = (V, E) hvor V, E er grafens kanter og toppunkter. Toppunkterne ifølge vores betragtning er Is (Kilde vertex – myrekoloni) og Id (Destination vertex – Fødevarekilde), De to kanter er OG1 og OG2 med længder L1 og L2 tildelt hver. Nu kan de tilknyttede feromonværdier (som indikerer deres styrke) antages at være R1 og R2 for hjørner E1og E2henholdsvis. For hver myre er startsandsynligheden for valg af vej således (mellem E1og E2) kan udtrykkes som følger:
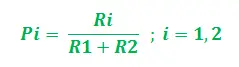
Åbenbart, hvis R1>R2, sandsynligheden for at vælge E1er højere og omvendt. Sig nu, mens du vender tilbage gennem denne korteste vej, Ejeg, opdateres feromonværdien for den tilsvarende sti. Opdateringen sker baseret på længden af stierne samt feromonens fordampningshastighed. Så opdateringen kan realiseres trinvist som følger:
- I overensstemmelse med stiens længde –
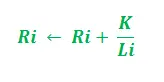
I ovenstående opdatering tjener i = 1, 2 og 'K' som en parameter for modellen. Desuden er opdateringen afhængig af stiens længde. Kortere stien, højere den tilføjede feromon. I overensstemmelse med fordampningshastigheden af feromon -
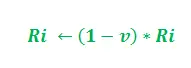
Parameteren 'v' hører til interval (0, 1], der regulerer feromonfordampningen. Yderligere er i = 1, 2.
Ved hver iteration placeres alle myrer ved kildetop Vs(myrekoloni). Efterfølgende flytter myrer fra Vstil Vd(fødekilde) efter trin 1. Dernæst gennemfører alle myrer deres hjemrejse og forstærker deres valgte vej baseret på trin 2.
fibonacci-serien i ca
Pseudokode:
Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>
Feromonopdateringen og fitnessberegningerne i ovenstående pseudokode kan findes gennem de trinvise implementeringer nævnt ovenfor.
Således er indførelsen af ACO-optimeringsteknikken etableret. Anvendelsen af ACO kan udvides til forskellige problemer, såsom de berømte TSP (Travelling Salesman Problem) .
Referencer:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf
