AVL træ:
AVL-træet er et selvbalancerende binært søgetræ ( BST ) hvor forskellen mellem højden af venstre og højre undertræ ikke kan være mere end en for alle noder.
Eksempel på AVL-træ:
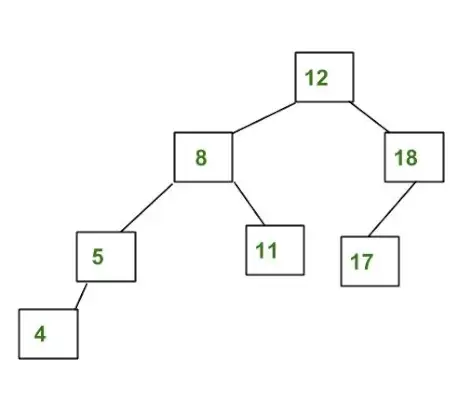
Ovenstående træ er AVL, fordi forskellene mellem højderne af venstre og højre undertræer for hver knude er mindre end eller lig med 1.
Eksempel på et træ, der IKKE er et AVL-træ:

Ovenstående træ er ikke AVL, fordi forskellene mellem højderne af venstre og højre undertræ for 8 og 12 er større end 1.
Hvorfor AVL-træer?
De fleste af BST-operationerne (f.eks. søgning, max, min, indsæt, slet... osv.) tager O(h) tid hvor h er højden af BST. Omkostningerne ved disse operationer kan blive På) for en skævt Binært træ . Hvis vi sørger for, at træets højde forbliver O(log(n)) efter hver indsættelse og sletning, så kan vi garantere en øvre grænse for O(log(n)) for alle disse operationer. Højden på et AVL-træ er altid O(log(n)) hvor n er antallet af noder i træet.
Indskud i AVL-træet:
For at sikre, at det givne træ forbliver AVL efter hver indsættelse, skal vi udvide standard BST-indsættelsesoperationen for at udføre en vis re-balancering.
Følgende er to grundlæggende handlinger, der kan udføres for at balancere en BST uden at krænke BST-egenskaben (taster (venstre)
- Venstre rotation
- Højre rotation
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x / Right Rotation / x T3 - - - - - - ->T1 og / <- - - - - - - / T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>Anbefalet praksis AVL-træindsættelse Prøv det!
Trin, der skal følges for indsættelse:
Lad den nyligt indsatte node være I
- Udfør standard BST indsætte for I .
- Startende fra I , rejs op og find den første ubalanceret node . Lade Med være den første ubalancerede knude, og Vær den barn af Med der kommer på vejen fra I til Med og x Vær den barnebarn af Med der kommer på vejen fra I til Med .
- Genbalancer træet ved at udføre passende rotationer på undertræet, der er rodfæstet med Med. Der kan være 4 mulige sager, der skal behandles som x,y og Med kan arrangeres på 4 måder.
- Følgende er de 4 mulige arrangementer:
- y er venstre underordnede af z, og x er venstre underordnede af y (venstre venstre bogstav)
- y er venstre barn af z, og x er højre barn af y (venstre højre bogstav)
- y er det rigtige barn af z og x er det rigtige barn af y (Right Right Case)
- y er det højre barn af z og x er det venstre barn af y (højre venstre bogstav)
Følgende er de operationer, der skal udføres i ovennævnte 4 tilfælde. I alle tilfælde behøver vi kun genbalancere undertræet rodfæstet med Med og hele træet bliver afbalanceret som højden af undertræet (Efter passende rotationer) rodfæstet med Med bliver det samme, som det var før indsættelsen.
1. Venstre venstre sag
T1, T2, T3 and T4 are subtrees. z y / / y T4 Right Rotate (z) x z / - - - - - - - - ->/ / x T3 T1 T2 T3 T4 / T1 T2>
2. Venstre Højre Case
z z x / / / y T4 Left Rotate (y) x T4 Right Rotate(z) y z / - - - - - - - - ->/ - - - - - - - -> / / T1 x y T3 T1 T2 T3 T4 / / T2 T3 T1 T2>
3. Højre højre sag
z y / / T1 y Left Rotate(z) z x / - - - - - - - ->/ / T2 x T1 T2 T3 T4 / T3 T4>
4. Højre venstre sag
z z x / / / T1 y Right Rotate (y) T1 x Left Rotate(z) z y / - - - - - - - - ->/ - - - - - - - -> / / x T4 T2 y T1 T2 T3 T4 / / T2 T3 T3 T4>
Illustration af indsættelse ved AVL-træ





Nærme sig:
Ideen er at bruge rekursiv BST insert, efter indsættelse får vi pointer til alle forfædre en efter en på en bottom-up måde. Så vi behøver ikke en overordnet pointer for at rejse op. Selve den rekursive kode rejser op og besøger alle forfædrene til den nyligt indsatte node.
Følg nedenstående trin for at implementere ideen:
- Udfør det normale BST indsættelse.
- Den aktuelle node skal være en af forfædrene til den nyligt indsatte node. Opdater højde af den aktuelle node.
- Få balancefaktoren (højde venstre undertræ – højde under træ til højre) af den aktuelle node.
- Hvis balancefaktoren er større end 1, så er den nuværende node ubalanceret, og vi er enten i Venstre Venstre sag eller venstre Højre sag . For at tjekke om det er venstre venstre sag eller ej, sammenligne den nyligt indsatte nøgle med nøglen i venstre undertræsrod .
- Hvis balancefaktoren er mindre end -1 , så er den aktuelle node ubalanceret, og vi er enten i højre højre tilfælde eller højre-venstre tilfælde. For at kontrollere, om det er højre højre sag eller ej, skal du sammenligne den nyligt indsatte nøgle med nøglen i højre undertrærod.
Nedenfor er implementeringen af ovenstående tilgang:
C++14
// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->højde;> }> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a:b;> }> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->nøgle = nøgle;> >node->venstre = NULL;> >node->højre = NULL;> >node->højde = 1;>// new node is initially> >// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->venstre;> >Node *T2 = x->højre;> > >// Perform rotation> >x->højre = y;> >y->venstre = T2;> > >// Update heights> >y->højde = max(højde(y->venstre),> >height(y->højre)) + 1;> >x->højde = max(højde(x->venstre),> >height(x->højre)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->højre;> >Node *T2 = y->venstre;> > >// Perform rotation> >y->venstre = x;> >x->højre = T2;> > >// Update heights> >x->højde = max(højde(x->venstre),> >height(x->højre)) + 1;> >y->højde = max(højde(y->venstre),> >height(y->højre)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->venstre) - højde(N->højre);> }> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->venstre = indsæt(node->venstre, nøgle);> >else> if> (key>node->tast)> >node->højre = indsæt(node->højre, nøgle);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->højde = 1 + max(højde(node->venstre),> >height(node->højre));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 &&-tast venstre->tast)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->højre->tast)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 &&-tast> node->venstre->tast)> >{> >node->venstre = venstreRotate(node->venstre);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->nøgle)> >{> >node->højre = højreRotate(node->højre);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >cout ' '; preOrder(root->venstre); forudbestilling(rod->højre); } } // Driverkode int main() { Node *root = NULL; /* Konstruktionstræ givet i ovenstående figur */ root = insert(root, 10); root = indsæt(rod, 20); root = indsæt(rod, 30); root = indsæt(rod, 40); root = indsæt(rod, 50); root = indsæt(rod, 25); /* Det konstruerede AVL-træ ville være 30 / 20 40 / 10 25 50 */ cout<< 'Preorder traversal of the ' 'constructed AVL tree is
'; preOrder(root); return 0; } // This code is contributed by // rathbhupendra> |
>
>
C
// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->højde;> }> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a:b;> }> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->nøgle = nøgle;> >node->venstre = NULL;> >node->højre = NULL;> >node->højde = 1;>// new node is initially added at leaf> >return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->venstre;> >struct> Node *T2 = x->højre;> > >// Perform rotation> >x->højre = y;> >y->venstre = T2;> > >// Update heights> >y->højde = max(højde(y->venstre),> >height(y->højre)) + 1;> >x->højde = max(højde(x->venstre),> >height(x->højre)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->højre;> >struct> Node *T2 = y->venstre;> > >// Perform rotation> >y->venstre = x;> >x->højre = T2;> > >// Update heights> >x->højde = max(højde(x->venstre),> >height(x->højre)) + 1;> >y->højde = max(højde(y->venstre),> >height(y->højre)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->venstre) - højde(N->højre);> }> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->venstre = indsæt(node->venstre, nøgle);> >else> if> (key>node->tast)> >node->højre = indsæt(node->højre, nøgle);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->højde = 1 + max(højde(node->venstre),> >height(node->højre));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 &&-tast venstre->tast)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->højre->tast)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 &&-tast> node->venstre->tast)> >{> >node->venstre = venstreRotate(node->venstre);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->nøgle)> >{> >node->højre = højreRotate(node->højre);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->nøgle);> >preOrder(root->venstre);> >preOrder(root->højre);> >}> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >' tree is
'>);> >preOrder(root);> > >return> 0;> }> |
>
>
Java
// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>b) ? a:b;> >}> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); else // Duplikatnøgler ikke tilladt returknude; /* 2. Opdater højden af denne forfaderknude */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Hent balancefaktoren for denne forfaderknude for at kontrollere, om denne node blev ubalanceret */ int balance = getBalance(node); // Hvis denne node bliver ubalanceret, så er der // 4 tilfælde Venstre Venstre Sagen if (balance> 1 && tast returner højreRotate(node); // Højre Højre Sagen if (balance<-1 && key>node.right.key) returner venstreRotate(node); // Left Right Case if (balance> 1 && key> node.left.key) { node.left = leftRotate(node.left); retur højreRotate(knudepunkt); } // Højre Venstre Sag if (balance<-1 && key node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + ' '); preOrder(node.left); preOrder(node.right); } } public static void main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ System.out.println('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal> |
>
>
Python3
# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 og tast returner self.rightRotate(root) # Case 2 - Right Right hvis balance<-1 and key>root.right.val: return self.leftRotate(root) # Case 3 - Left Right hvis balance> 1 og nøgle> root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root ) # Tilfælde 4 - Højre Venstre hvis balance<-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak> |
>
>
C#
// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>b) ? a:b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); else // Duplikatnøgler ikke tilladt returknude; /* 2. Opdater højden af denne forfaderknude */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Hent balancefaktoren for denne forfaderknude for at kontrollere, om denne node blev ubalanceret */ int balance = getBalance(node); // Hvis denne node bliver ubalanceret, så er der // 4 tilfælde Venstre Venstre Case if (balance> 1 && tast returner rightRotate(node); // Right Right Case if (balance node.right.key) return leftRotate(node) ; // Left Right Case if (balance> 1 && key> node.left.key) { node.left = leftRotate(node.left return rightRotate(node);<-1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + ' '); preOrder(node.left); preOrder(node.right); } } // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ Console.Write('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed // by PrinciRaj1992> |
>
>
Javascript
> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>b ? a:b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if> (key node.left = this.insert(node.left, key); else if (key>node.key) node.right = this.insert(node.right, key); // Duplikatnøgler ikke tilladt ellers returner node; /* 2. Opdater højden af denne forfaderknude */ node.height = 1 + this.max(this.height(node.left), this.height(node.right)); /* 3. Hent balancefaktoren for denne forfaderknude for at kontrollere, om denne node blev ubalanceret */ var balance = this.getBalance(node); // Hvis denne node bliver ubalanceret, så er der // 4 tilfælde Venstre Venstre Case if (balance> 1 && tast returner this.rightRotate(node); // Right Right Case if (balance node.right.key) returner dette. leftRotate(node); // Left Right Case if (balance> 1 && key> node.left.key) { node.left = this.leftRotate(node.left } // Right; Venstre sag hvis (balance<-1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + ' '); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ document.write( 'Preorder traversal of the ' + 'constructed AVL tree is ' ); tree.preOrder(tree.root);> |
>
>Produktion
Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>
Kompleksitetsanalyse
Tidskompleksitet: O(log(n)), til indsættelse
Hjælpeplads: O(1)
kommando touch i linux
Rotationsoperationerne (venstre- og højredrejning) tager konstant tid, da kun nogle få pointere bliver ændret der. At opdatere højden og få balancefaktoren tager også konstant tid. Så tidskompleksiteten af AVL-indsatsen forbliver den samme som BST-indsatsen, som er O(h), hvor h er højden af træet. Da AVL-træet er afbalanceret, er højden O(Logn). Så tidskompleksiteten af AVL-indsættelsen er O(Logn).
Sammenligning med Red Black Tree:
AVL-træet og andre selvbalancerende søgetræer som Red Black er nyttige til at få alle grundlæggende handlinger udført på O(log n) tid. AVL-træerne er mere afbalancerede sammenlignet med rød-sorte træer, men de kan forårsage flere rotationer under indsættelse og sletning. Så hvis din ansøgning involverer mange hyppige indsættelser og sletninger, så bør røde sorte træer foretrækkes. Og hvis indsættelser og sletninger er mindre hyppige, og søgning er den hyppigere operation, så bør AVL-træet foretrækkes frem for Red Black Tree .
Følgende er indlægget til sletning i AVL Tree:
AVL træ | Sæt 2 (sletning)
