Introduktion:

En halvadder er et digitalt logisk kredsløb, der udfører binær addition af to single-bit binære tal. Den har to indgange, A og B, og to udgange, SUM og CARRY. SUM-outputtet er den mindst signifikante bit (LSB) af resultatet, mens CARRY-output er den mest signifikante bit (MSB) af resultatet, hvilket indikerer, om der var en overførsel fra tilføjelsen af ​​de to inputs. Halvadderen kan implementeres ved hjælp af grundlæggende porte såsom XOR og AND gates.

Sikker på, her er en mere dybdegående forklaring af halvadderkredsløbet:

Den halve adder er en grundlæggende byggeklods til mere komplekse adderkredsløb såsom fuld addere og multiple-bit addere. Den udfører binær addition af to enkelt-bit input, A og B, og giver to udgange, SUM og CARRY.

SUM-outputtet er den mindst signifikante bit (LSB) af resultatet, som er XOR for de to input A og B. XOR-porten implementerer additionsoperationen for binære cifre, hvor der kun genereres et 1 i SUM-outputtet, når én af inputs er 1.

java xor

CARRY-outputtet er den mest signifikante bit (MSB) af resultatet, hvilket indikerer, om der var en overførsel fra tilføjelsen af ​​de to input. CARRY-udgangen er AND af de to indgange A og B. AND-porten genererer kun et 1 i CARRY-udgangen, når begge indgange er 1.

Halv adder (HA):

Halv adder er det enkleste af alle adderkredsløb. Halvadder er et aritmetisk kombinationskredsløb, der tilføjer to tal og producerer en sumbit (s) og en bærebit (c) begge som output. Tilføjelsen af ​​2 bits udføres ved hjælp af et kombinationskredsløb kaldet en halvadder. Inputvariablerne er augend- og addend-bits og outputvariabler er sum & carry-bits. A og B er de to inputbits.

lad os betragte to inputbits A og B, så er sumbit (s) X-ELLER af A og B. Det fremgår tydeligt af funktionen af ​​en halvadder, at den kræver en X-OR-port og en AND-port til sin konstruktion.

Sandhedstabel:

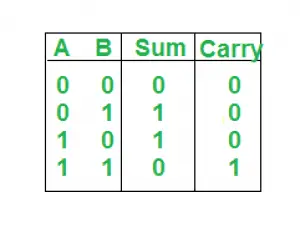
java indeks af

Her udfører vi to operationer Sum og Carry, så vi har brug for to K-maps en til hver for at udlede udtrykket.

Logisk udtryk:

For summen:

Sum = A XOR B

Til transport:

Bær = A OG B

Implementering:

Bemærk: Halvadder har kun to indgange, og der er ingen mulighed for at tilføje en carry, der kommer fra de lavere ordens bit, når multiaddition udføres.

Fordele og ulemper ved Half Adder i digital logik:

Fordele ved Half Adder i digital logik:

1. Enkelhed: En halv hugorm er et ligetil kredsløb, der kræver et par grundlæggende dele som XOR OG indgange. Det er ikke svært at udføre og kan bruges i adskillige avancerede rammer.

Java gør ikke

2. Hastighed: Halvhugormen arbejder ekstremt hurtigt, hvilket gør den rimelig at bruge i hurtige computeriserede kredsløb.

Ulemper ved Half Adder i digital logik:

1. Begrænset anvendelighed: Den halve hugorm kan tilføje to numre i ét stykke og producere en total og en transportbit. Det kan ikke udføre udvidelse af multi-bit-numre, hvilket kræver brug af yderligere indviklede kredsløb som fulde addere.

2. Manglende formidlingsoplysninger: Den halve slange har ikke et formidlingsinput, hvilket begrænser dens værdi i mere forunderlige udvidelsesopgaver. Et formidlingsinput er vigtigt for at udføre udvidelse af multi-bit-tal og for at kæde adskillige addere sammen.

3. Udsættelse af udbredelse: Halvslangekredsløbet har en spredningsforsinkelse, som er den tid det tager for resultatet at ændre sig i lyset af en justering af infoen. Dette kan forårsage timing problemer i computeriserede kredsløb, især i hurtige rammer.

Anvendelse af Half Adder i digital logik:

1. Aritmetiske kredsløb: Halvaddere bruges i tal-knasende kredsløb for at tilføje dobbelttal. På det tidspunkt, hvor forskellige halvaddere er tilknyttet i en kæde, kan de tilføje multi-bit dobbelttal.

2. Datahåndtering: Halvaddere bruges i informationshåndteringsapplikationer som computerstyret signalhåndtering, informationskryptering og fejljustering.

3. Adresseoptrævling: I hukommelse, der har tendens til, anvendes halvaddere i adressedechifreringskredsløb for at frembringe placeringen af ​​et bestemt hukommelsesområde.

4. Encoder- og dekoderkredsløb: Halvaddere bruges i indkoder- og dekoderkredsløb til computeriserede korrespondancerammer.

også model

5.Multipleksere og demultipleksere: Halvaddere bruges i multipleksere og demultipleksere til at vælge og kursusinformation.

6. Tællere: Halvhuggormer bruges i tællere for at øge antallet med én.