Problemer med regression og probabilistisk klassifikation kan løses ved hjælp af Gauss-processen (GP), en overvåget læringsteknik. Da hver Gauss-proces kan opfattes som en uendelig-dimensionel generalisering af multivariat Gaussiske fordelinger , udtrykket Gauss optræder i navnet. Vi vil diskutere Gaussiske processer for regression i dette indlæg, som også omtales som Gaussisk procesregression (GPR). Adskillige problemer i den virkelige verden inden for materialevidenskab, kemi, fysik og biologi er blevet løst ved brug af GPR.
Indholdsfortegnelse
- Gaussisk procesregression (GPR)
- Nøglebegreber for Gaussisk procesregression (GPR)
- Matematisk koncept for Gaussisk procesregression (GPR)
- Implementering af Gaussisk proces i Python
Gaussisk procesregression (GPR)
Gaussisk procesregression (GPR) er en kraftfuld og fleksibel ikke-parametrisk regressionsteknik, der bruges i maskinelæring og Statistikker . Det er især nyttigt, når man håndterer problemer, der involverer kontinuerlige data, hvor forholdet mellem inputvariable og output ikke er eksplicit kendt eller kan være komplekst. GPR er en Bayesiansk tilgang, der kan modellere sikkerhed i forudsigelser, hvilket gør det til et værdifuldt værktøj til forskellige applikationer, herunder optimering, tidsserieprognoser og mere. GPR er baseret på konceptet om en Gauss-proces, som er en samling af stokastiske variable, hvoraf ethvert endeligt antal har en fælles Gauss-fordeling. En Gauss-proces kan opfattes som en fordeling af funktioner.
Nøglebegreber for Gaussisk procesregression (GPR)
Gaussain-processen
En ikke-parametrisk, probabilistisk model kaldet a Gaussisk proces (GP) bruges i statistik og maskinlæring til regression, klassificering og kvantificering af usikkerhed. Den afbilder en gruppe af stokastiske variable, som hver har en fælles Gauss-fordeling og kan have et endeligt tal. Praktiserende læger er en alsidig og effektiv teknik til at modellere indviklede sammenhænge i data og producere prognoser med tilhørende usikkerhed.
Karakteristika for Gaussiske processer :
- Ikke-parametrisk natur : Praktiserende læger kan tilpasse sig kompleksiteten af dataene, fordi de ikke er afhængige af et bestemt antal modelparametre
- Probabilistiske forudsigelser : Forudsigelser fra praktiserende læger kan kvantificeres, fordi de leverer forudsigelser som sandsynlighedsfordelinger.
- Interpolation og udjævning : GP'er er nyttige til støjende eller uregelmæssigt samplede data, fordi de er gode til at udjævne støjende data og interpolere mellem datapunkter.
- Marginalisering af hyperparametre : Ved at eliminere kravet om eksplicit hyperparameter tweaking, marginaliserer de over hyperparametre, hvilket gør modellen enklere.
Gennemsnitlig funktion
Den forudsagte værdi af den funktion, der modelleres ved hvert inputpunkt, er repræsenteret af middel funktion i Gaussiske processer (praktiserende læger). Det fungerer som en grundlæggende formodning vedrørende den underliggende datastruktur. Middelfunktionen er ofte sat til nul som standard, ikke nødvendigvis og kan ændres baseret på dataegenskaber eller domæneekspertise. Ved at påvirke prognosernes centrale tendens hjælper det praktiserende læger med at identificere mønstre eller tendenser i dataene. Praktiserende læger giver probabilistiske forudsigelser, der indeholder usikkerhed såvel som punktestimater ved at inkludere middelfunktionen
Kovarians (kerne) funktion
Det kovariansfunktion , også kaldet kernefunktionen, måler, hvor ens inputdatapunkterne er hinanden i Gaussiske processer (GP'er). Det er væsentligt for at karakterisere adfærden af GP-modellen, hvilket påvirker valget af funktioner fra den tidligere distribution. Kovariansfunktionen måler parvise ligheder for at fastslå korrelationen mellem funktionsværdier. GP'er kan tilpasse sig en bred vifte af datamønstre, fra glatte tendenser til komplekse strukturer, fordi forskellige kernefunktioner fanger forskellige slags korrelationer. Modellens ydeevne kan i høj grad påvirkes af kernevalget.
Tidligere distributioner
Det forudgående distribution , i Gaussiske processer (GP'er), er vores forståelse af funktioner forud for observation af data. Normalt er det beskrevet af en kovariansfunktion (kerne) og en middelfunktion. Hvor kovariansfunktionen beskriver ligheden eller korrelationen mellem funktionsværdier ved forskellige inputpunkter, koder middelfunktionen vores tidligere forventninger. Dette bruges på forhånd af praktiserende læger til at skabe en fordeling over funktioner. Hos praktiserende læger kan priors vælges til at repræsentere datausikkerhed, integrere domæneviden eller angive glathed.
Posteriore fordelinger
Gaussiske processer senere distribution viser vores reviderede antagelser om funktioner efter dataobservation. Den sammensætter sandsynligheden for dataene givet funktionen og den tidligere fordeling. Den posteriore i GP-regression tilbyder en fordeling over funktioner, der passer bedst til de observerede data. Ved at tillade probabilistiske forudsigelser og kvantificering af usikkerhed afspejler den posteriore fordeling afvejningen mellem de tidligere overbevisninger, der er lagret i den tidligere fordeling, og informationen leveret af dataene.
Matematisk koncept for Gaussisk procesregression (GPR)
Til regressionsopgaver anvendes en ikke-parametrisk, probabilistisk maskinlæringsmodel kaldet Gaussian Process (GP) regression. Når man modellerer indviklede og tvetydige interaktioner mellem input- og outputvariabler, er det et potent værktøj. En multivariat Gauss-fordeling antages at producere datapunkterne i GP-regression, og målet er at udlede denne fordeling.
GP-regressionsmodellen har følgende matematiske udtryk. Lad os antage x1, x2,…..,xner inputdatapunkterne, hvor x hører til reelle tal(-2,-1,0,1…), (xjeg
Lad os antage y1, og2 ,……., ogner outputværdierne, hvor yjeghører til et reelt tal (yjeg
GP-regressionsmodellen gør den antagelse, at en Gauss-proces med en middelfunktion (
Derefter, ved et sæt af teststeder x*, er fordelingen af f givet ved:
Typisk bruges kernefunktioner til at definere middelfunktionen og kovariansfunktionen. Som en illustration beskrives den kvadratiske eksponentielle kerne, der ofte anvendes, som:
q3 måneder
Hvor,
k(x_{i}, x_{j}) = Kernefunktionen er repræsenteret af dette, og den beregner korrelationen eller ligheden mellem to inputdatapunkter, xjegog xj.sigma^2 = Kernens variansparameter er dette. Det etablerer kernefunktionens skala eller lodrette spredning. Det regulerer, hvor stærkt datapunkterne er korrelerede. En højeresigma^2 giver en kernefunktion med større varians.- exp: Den eksponentielle funktion er ansvarlig for at hæve e til argumentets magt.
||x_{i} – x_{j}||^2 : Forskellen mellem inputdatapunkterne, xjegog xj, er den kvadratiske euklidiske afstand. Den geometriske adskillelse mellem punkterne i trækrummet måles.- l2: Dette er en repræsentation af kernens længdeskala eller karakteristiske længde. Det regulerer den hastighed, hvormed kernefunktionen forringes, når datapunkter er længere fra hinanden. Et lavere l får kernen til at nedbrydes hurtigere.
GP-regressionsmodellen anvender Bayesiansk inferens til at bestemme fordelingen af f, der med størst sandsynlighed har produceret dataene givet et sæt træningsdata (x, y). For at gøre dette skal den posteriore fordeling af f givet data beregnes, som er defineret som følger:
hvor den marginale sandsynlighed for dataene er p(y|x), den forudgående fordeling af f er p(f), og sandsynligheden for dataene givet funktionen f er (y|x,f).
Efter at have lært den posteriore fordeling af f, beregner modellen den posteriore prædiktive fordeling for at lave forudsigelser ved yderligere testpunkter x*. Det kan defineres som følger:
Hvor,
p(f^*|x*, y, x) = Dette viser, givet træningsdataene y og x, den betingede sandsynlighed for de forudsagte funktionsværdier f*ved et nyt inputpunkt x*For at sige det på en anden måde er det sandsynlighedsfordelingen over alle potentielle funktionsværdier på det nye inputsted x*, betinget af de observerede data y og deres matchende inputplaceringer x.int p(f^*|x^*, f)p(f|y,x)df = Et integral anvendes i dette afsnit af ligningen til at bestemme den betingede sandsynlighed. Integralet omfatter alle potentielle værdier af funktionen f.p(f^*|x^*, f) = Dette er den betingede sandsynlighedsfordeling af de forventede funktionsværdier f*ved x*, givet funktionsværdierne f på nogle mellemliggende steder.p(f|y,x) = Givet de observerede data (y) og deres inputplaceringer (x), er dette den betingede sandsynlighedsfordeling af funktionsværdierne (f).
For opgaver som usikkerhedsbevidst beslutningstagning og aktiv læring tilbyder denne fordeling et mål for forudsigelsens usikkerhed, hvilket kan være nyttigt.
Trin i Gaussisk procesregression
- Dataindsamling : Saml input-output dataparrene til dit regressionsproblem.
- Vælg en kernefunktion : Vælg en passende kovariansfunktion (kerne), der passer til dit problem. Valget af kerne påvirker formen af de funktioner, som GPR kan modellere.
- Parameter optimering : Estimer hyperparametrene for kernefunktionen ved at maksimere sandsynligheden for dataene. Dette kan gøres ved hjælp af optimeringsteknikker som gradientnedstigning.
- Forudsigelse: Givet et nyt input, brug den trænede GPR-model til at lave forudsigelser. GPR giver både det forudsagte gennemsnit og den tilhørende usikkerhed (varians).
Implementering af Gaussisk procesregression (GPR)
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Produktion:
I denne kode skal du først generere nogle eksempeldatapunkter med tilføjet støj, derefter definere en RBF-kerne og oprette en Gaussisk procesregressor med det. Modellen trænes på træningsdataene og bruges til at lave forudsigelser på testdataene. Til sidst visualiseres resultaterne med et plot, der viser træningsdata, det forudsagte gennemsnit og 95 % konfidensintervallet.
Implementering af Gaussisk proces i Python
Scikit Lær
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> De nødvendige biblioteker til Gaussian Process Regression (GPR) i Python importeres af denne kode; disse er SciPy for lineære algebrafunktioner, NumPy til numeriske operationer, og Matplotlib til datavisualisering. For at sikre, at den er kompatibel med de nødvendige pakker, verificerer den desuden versionen af Python og udskriver den sammen med versionerne af NumPy og scikit-learn (sklearn).
Kernevalg
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Produktion:
[RBF(længde_skala=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(length_scale=1, periodicity=10),
PunktProdukt(sigma_0=1) ** 2,
Maternal(længde_skala=1, nu=1,5)]
Koden angiver antallet af teststeder (n) og initialiserer en tilfældigt frø . For at vise de valgte kerner, genererer den en liste over flere kernefunktioner og udskriver listen.
Kernel sammenligning og visualisering
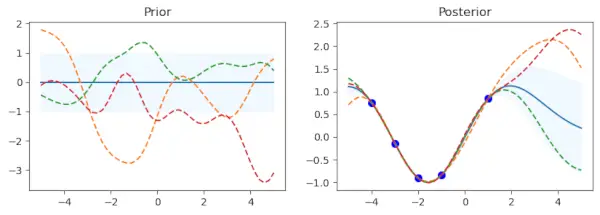
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Produktion:
RBF
gp.kernel_ RBF(længde_skala=1,93)
gp.log_marginal_likelihood: -3.444937833462133
-------------------------------------------------- -
Rationel kvadratisk

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1,93)
gp.log_marginal_likelihood: -3.4449718909150966
--------------------------------------------------
ExpSineSquared

gp.kernel_ ExpSineSquared(length_scale=0,000524, periodicitet=2,31e+04)
gp.log_marginal_likelihood: -3.4449381454930217
--------------------------------------------------
Prik produkt

gp.kernel_ DotProduct(sigma_0=0,998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------
Moderlig

gp.kernel_ Matern(length_scale=1,99, nu=1,5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------
Koden starter med at gå over de forskellige kernefunktioner, der er angivet i kernel_-listen. En Gaussian Process Regressor (gp) laves ved at bruge den særlige kerne for hver kerne. For den Gaussiske proces etablerer dette kovariansstrukturen. For at vurdere den tidligere fordeling etableres et sæt testinputpunkter kaldet x_test, med værdier fra -5 til 5. Dette sæt punkter transformeres til en kolonnevektor.
Ved at bruge gp.predict-metoden bestemmes den tidligere fordelings middelværdi (mu_prior) og standardafvigelse (sd_prior) ved hvert testpunkt. Standardafvigelsesværdier anmodes om ved at bruge return_std=True-indstillingen. gp.sample_y (x_test, 3) bruges til at få tre funktionseksempler fra den tidligere fordeling.
Det første subplot viser den tidligere fordelings middelværdi, med standardafvigelsen repræsenteret af et skraveret område. Prøverne er overlejret som stiplede linjer, mens middelværdien vises som en ubrudt linje. Der er et underplot kaldet Prior. Der er et defineret sæt træningsdatapunkter (x_train) og målværdier (y_train), der følger med dem. Gaussisk procesmodellen er tilpasset ved hjælp af disse punkter (gp.fit(x_train, y_train)). Fem datapunkter med tilsvarende sinusværdier udgør træningsdataene i denne kode.
Efter træningsdatatilpasningsfasen beregner proceduren den posteriore fordelings middelværdi (mu_post) og standardafvigelse (sd_post) for de samme testpunkter (x_test). gp.sample_y(x_test, 3) bruges også til at producere funktionsprøver fra den posteriore fordeling. Det andet subplot overlejrer de samplede funktioner som stiplede linjer og viser middelværdien af den posteriore fordeling, skraveret med standardafvigelsen. Træningsdatapunkterne er plottet med blåt. Underplottet har navnet Posterior.
For at se de foregående og posteriore plots for den aktuelle kerne og få en visuel forståelse af modellens adfærd, skal du kalde Matplotlibs plt.show() funktion.
Koden viser detaljer om den aktuelle kerne, såsom gp.kernel_, som angiver den aktuelle kerne, der bruges, og gp.log_marginal_likelihood (gp.kernel_.theta), som giver log marginal sandsynlighed for, at modellen bruger den aktuelle kerne, efter hvert sæt af tidligere og posteriore plots.
Fordele ved Gaussisk procesregression (GPR)
Gaussisk procesregression (GPR) har en række fordele i en række applikationer:
- GPR giver en probabilistisk ramme for regression, hvilket betyder, at den ikke kun giver punktestimater, men også giver usikkerhedsestimater for forudsigelser.
- Det er meget fleksibelt og kan fange komplekse sammenhænge i dataene.
- GPR kan tilpasses til forskellige applikationer, herunder tidsserieprognoser, optimering og Bayesiansk optimering.
Udfordringer ved Gaussisk procesregression (GPR)
- GPR kan være beregningsmæssigt dyrt, når man har at gøre med store datasæt, da inversion af en kovariansmatrix er påkrævet.
- Valget af kernefunktionen og dens hyperparametre kan påvirke modellens ydeevne betydeligt.
Gode eksempler på GPR-applikationer
- Aktiepris forudsigelse: GPR kan bruges til at modellere og forudsige aktiekurser under hensyntagen til volatiliteten og usikkerheden på de finansielle markeder.
- Computereksperimenter: GPR er nyttig til at optimere komplekse simuleringer ved at modellere input-output-forhold og identificere de mest indflydelsesrige parametre.
- Anomali detektion: GPR kan anvendes til anomalidetektion, hvor det identificerer usædvanlige mønstre i tidsseriedata ved at fange normale datafordelinger.
Konklusion
Som konklusion er Gaussisk procesregression et værdifuldt værktøj til dataanalyse og forudsigelse i situationer, hvor det er vigtigt at forstå usikkerheden i forudsigelser. Ved at udnytte probabilistisk modellering og kernefunktioner kan GPR give nøjagtige og fortolkelige resultater. Det er dog afgørende at overveje de beregningsmæssige omkostninger og behovet for ekspertinput, når GPR implementeres i praksis.
hvad er struktur i datastruktur
