Givet et gitter med tal finder den maksimale længde slangesekvens og udskriver den. Hvis der findes flere slangesekvenser med den maksimale længdeudskrivning af dem.
hvor gammel er pete davidson
En slangesekvens består af tilstødende tal i gitteret, således at antallet til højre eller antallet nedenfor er +1 eller -1 dets værdi. Hvis du f.eks. Er på stedet (x y) i gitteret, kan du enten bevæge dig til højre, dvs. (x y+1), hvis dette tal er ± 1 eller bevæger sig ned, dvs. (x+1 y), hvis dette tal er ± 1.
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Nedenfor viser figur alle mulige stier:
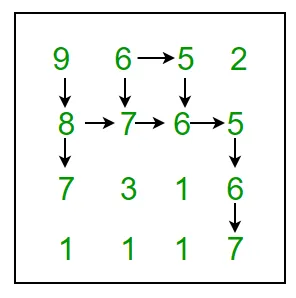
Vi anbefaler dig kraftigt at minimere din browser og prøve dette selv først.
Ideen er at bruge dynamisk programmering. For hver celle i matrixen holder vi maksimal længde af en slange, der ender i den nuværende celle. Den maksimale længde slangesekvens vil have maksimal værdi. Den maksimale værdicelle svarer til hale af slangen. For at udskrive slangen er vi nødt til at backtrack fra Tail helt tilbage til Snakes hoved.
fordelene ved instagram til personlig brug
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Nedenfor er implementeringen af ideen
C++// C++ program to find maximum length // Snake sequence and print it #include
// Java program to find maximum length // Snake sequence and print it import java.util.*; class GFG { static int M = 4; static int N = 4; static class Point { int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int grid[][] int mat[][] int i int j) { List<Point> path = new LinkedList<>(); Point pt = new Point(i j); path.add(0 pt); while (grid[i][j] != 0) { if (i > 0 && grid[i][j] - 1 == grid[i - 1][j]) { pt = new Point(i - 1 j); path.add(0 pt); i--; } else if (j > 0 && grid[i][j] - 1 == grid[i][j - 1]) { pt = new Point(i j - 1); path.add(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int mat[][]) { // table to store results of subproblems int [][]lookup = new int[M][N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.abs(mat[i - 1][j] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i - 1][j] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.abs(mat[i][j - 1] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i][j - 1] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } } } } System.out.print('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); System.out.print('Snake sequence is:'); for (Point it : path) System.out.print('n' + mat[it.x][it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void main(String[] args) { int mat[][] = {{9 6 5 2} {8 7 6 5} {7 3 1 6} {1 1 1 7}}; findSnakeSequence(mat); } } // This code is contributed by 29AjayKumar
// C# program to find maximum length // Snake sequence and print it using System; using System.Collections.Generic; class GFG { static int M = 4; static int N = 4; public class Point { public int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int[ ] grid int[ ] mat int i int j) { List<Point> path = new List<Point>(); Point pt = new Point(i j); path.Insert(0 pt); while (grid[i j] != 0) { if (i > 0 && grid[i j] - 1 == grid[i - 1 j]) { pt = new Point(i - 1 j); path.Insert(0 pt); i--; } else if (j > 0 && grid[i j] - 1 == grid[i j - 1]) { pt = new Point(i j - 1); path.Insert(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int[ ] mat) { // table to store results of subproblems int[ ] lookup = new int[M N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.Abs(mat[i - 1 j] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i - 1 j] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.Abs(mat[i j - 1] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i j - 1] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } } } } Console.Write('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); Console.Write('Snake sequence is:'); foreach(Point it in path) Console.Write('n' + mat[it.x it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void Main(String[] args) { int[ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence(mat); } } // This code is contributed by Princi Singh
def snakesequence(S m n): sequence = {} DP = [[1 for x in range(m+1)] for x in range(n+1)] a b maximum = 0 0 0 position = [0 0] for i in range(0 n+1): for j in range(0 m+1): a b = 0 0 p = 'initial' if(i > 0 and abs(S[i][j] - S[i-1][j]) == 1): a = DP[i-1][j] if(j > 0 and abs(S[i][j] - S[i][j-1]) == 1): b = DP[i][j-1] if a != 0 and a >= b: p = str(i-1) + ' ' + str(j) elif b != 0: p = str(i) + ' ' + str(j-1) q = str(i) + ' ' + str(j) sequence[q] = p DP[i][j] = DP[i][j] + max(a b) if DP[i][j] >= maximum: maximum = DP[i][j] position[0] = i position[1] = j snakeValues = [] snakePositions = [] snakeValues.append(S[position[0]][position[1]]) check = 'found' str_next = str(position[0]) + ' ' + str(position[1]) findingIndices = sequence[str_next].split() while(check == 'found'): if sequence[str_next] == 'initial': snakePositions.insert(0 str_next) check = 'end' continue findingIndices = sequence[str_next].split() g = int(findingIndices[0]) h = int(findingIndices[1]) snakeValues.insert(0 S[g][h]) snake_position = str(g) + ' ' + str(h) snakePositions.insert(0 str_next) str_next = sequence[str_next] return [snakeValues snakePositions] S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] m = 3 n = 3 seq = snakesequence(S m n) for i in range(len(seq[0])): print(seq[0][i] '' seq[1][i].split())
function snakesequence(S m n) { let sequence = {} let DP = new Array(n + 1) for (var i = 0; i <= n; i++) DP[i] = new Array(m + 1).fill(1) let a = 0 b = 0 maximum = 0 let position = [0 0] for (var i = 0; i <= n; i++) { for (var j = 0; j <= m; j++) { a = 0 b = 0 let p = 'initial' if(i > 0 && Math.abs(S[i][j] - S[i-1][j]) == 1) a = DP[i-1][j] if(j > 0 && Math.abs(S[i][j] - S[i][j-1]) == 1) b = DP[i][j-1] if (a != 0 && a >= b) p = String(i-1) + ' ' + String(j) else if (b != 0) p = String(i) + ' ' + String(j-1) let q = String(i) + ' ' + String(j) sequence[q] = p DP[i][j] = DP[i][j] + Math.max(a b) if (DP[i][j] >= maximum) { maximum = DP[i][j] position[0] = i position[1] = j } } } let snakeValues = [] let snakePositions = [] snakeValues.push(S[position[0]][position[1]]) let check = 'found' let String_next = String(position[0]) + ' ' + String(position[1]) let findingIndices = sequence[String_next].split(' ') while(check == 'found') { if (sequence[String_next] == 'initial') { snakePositions.unshift(String_next) check = 'end' continue } findingIndices = sequence[String_next].split(' ') let g = parseInt(findingIndices[0]) let h = parseInt(findingIndices[1]) snakeValues.unshift(S[g][h]) let snake_position = String(g) + ' ' + String(h) snakePositions.unshift(String_next) String_next = sequence[String_next] } return [snakeValues snakePositions] } // Driver Code let S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] let m = 3 let n = 3 let seq = snakesequence(S m n) for (var i = 0; i < seq[0].length; i++) console.log(seq[0][i] + '' seq[1][i].split(' '))
Produktion
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Tidskompleksitet af ovenstående opløsning er O (M*N). Hjælpeplads anvendt af ovenstående opløsning er O (M*N). Hvis vi ikke er forpligtet til at udskrive slangepladsen, kan det reduceres yderligere til O (n), da vi kun bruger resultatet fra sidste række.
konstruktører i java
