Givet en særligt binært træ hvis bladknuder er forbundet til at danne a cirkulær dobbeltforbundet liste opgaven er at finde højde af træet.
Eksempler:
Input:

Produktion: 2
Forklaring: Højden af det binære træ efter genkendelse af bladknuderne er 2. I ovenstående er binære træer 6 5 og 4 bladknuder, og de danner en cirkulær dobbeltforbundet liste. Her vil venstre pointer på bladknudepunktet fungere som en tidligere pointer på en cirkulær dobbeltforbundet liste, og dens højre pointer vil fungere som næste pointer på en cirkulær dobbelt linket liste.Input:
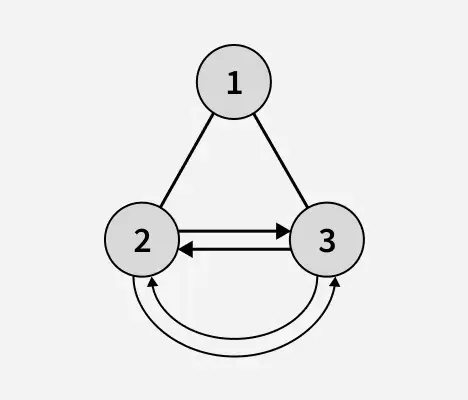
Produktion: 1
Forklaring: Højden af binært træ efter genkendelse af bladknuderne er 1. I ovenstående er binære træ 2 og 3 bladknuder, og de danner en cirkulær dobbeltforbundet liste.
Nærme sig :
C++Tanken er at følge lignende tilgang som vi gør for at finde højden af et normalt binært træ . Vi rekursivt beregne højde af venstre og højre undertræer af en node og tildele højde til noden som max af højden af to børn plus 1. Men venstre og højre barn af en bladknude er nul for normale binære træer. Men her er bladknude en cirkulær dobbeltforbundet listeknude. Så for at en node skal være en bladknude, tjekker vi om nodens venstre til højre peger på node og dens højre venstre peger også på node sig selv.
// C++ program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list #include
// C program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list #include
// Java program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list class Node { int data; Node left right; Node(int x) { data = x; left = null; right = null; } } class GfG { // function to check if given // node is a leaf node or node static boolean isLeaf(Node node) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node.left != null && node.left.right == node && node.right != null && node.right.left == node; } // Compute the height of a tree static int findTreeHeight(Node node) { // if node is NULL return -1. if (node == null) return -1; // if node is a leaf node return 0 if (isLeaf(node)) return 0; // compute the depth of each subtree and take maximum return 1 + Math.max(findTreeHeight(node.left) findTreeHeight(node.right)); } public static void main(String[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.left.left.left = new Node(6); // Given tree contains 3 leaf nodes Node l1 = root.left.left.left; Node l2 = root.left.right; Node l3 = root.right; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1.right = l2; l2.right = l3; l3.right = l1; // set prev pointer of linked list l3.left = l2; l2.left = l1; l1.left = l3; System.out.println(findTreeHeight(root)); } }
# Python program to calculate height of a special tree # whose leaf nodes forms a circular doubly linked list class Node: def __init__(self data): self.data = data self.left = None self.right = None # function to check if given # node is a leaf node or node def isLeaf(node): # For a node to be a leaf node it should # satisfy the following two conditions: # 1. Node's left's right pointer should be # current node. # 2. Node's right's left pointer should be # current node. # If one condition is met it is guaranteed # that the other condition is also true. return (node.left and node.left.right == node and node.right and node.right.left == node) # Compute the height of a tree def findTreeHeight(node): # if node is NULL return -1. if node is None: return -1 # if node is a leaf node return 0 if isLeaf(node): return 0 # compute the depth of each subtree and take maximum return 1 + max(findTreeHeight(node.left) findTreeHeight(node.right)) if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.left.left.left = Node(6) # Given tree contains 3 leaf nodes l1 = root.left.left.left l2 = root.left.right l3 = root.right # create circular doubly linked list out of # leaf nodes of the tree # set next pointer of linked list l1.right = l2 l2.right = l3 l3.right = l1 # set prev pointer of linked list l3.left = l2 l2.left = l1 l1.left = l3 print(findTreeHeight(root))
// C# program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list using System; class Node { public int data; public Node left right; public Node(int x) { data = x; left = null; right = null; } } class GfG { // function to check if given // node is a leaf node or node static bool isLeaf(Node node) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node.left != null && node.left.right == node && node.right != null && node.right.left == node; } // Compute the height of a tree static int findTreeHeight(Node node) { // if node is NULL return -1. if (node == null) return -1; // if node is a leaf node return 0 if (isLeaf(node)) return 0; // compute the depth of each subtree and take maximum return 1 + Math.Max(findTreeHeight(node.left) findTreeHeight(node.right)); } static void Main(string[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.left.left.left = new Node(6); // Given tree contains 3 leaf nodes Node l1 = root.left.left.left; Node l2 = root.left.right; Node l3 = root.right; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1.right = l2; l2.right = l3; l3.right = l1; // set prev pointer of linked list l3.left = l2; l2.left = l1; l1.left = l3; Console.WriteLine(findTreeHeight(root)); } }
// JavaScript program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list class Node { constructor(data) { this.data = data; this.left = null; this.right = null; } } // function to check if given // node is a leaf node or node function isLeaf(node) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node.left && node.left.right === node && node.right && node.right.left === node; } // Compute the height of a tree function findTreeHeight(node) { // if node is NULL return -1. if (node === null) return -1; // if node is a leaf node return 0 if (isLeaf(node)) return 0; // compute the depth of each subtree and take maximum return 1 + Math.max(findTreeHeight(node.left) findTreeHeight(node.right)); } const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.left.left.left = new Node(6); // Given tree contains 3 leaf nodes const l1 = root.left.left.left; const l2 = root.left.right; const l3 = root.right; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1.right = l2; l2.right = l3; l3.right = l1; // set prev pointer of linked list l3.left = l2; l2.left = l1; l1.left = l3; console.log(findTreeHeight(root));
Produktion
3
Tidskompleksitet: O(n) hvor n er antallet af noder.
Hjælpeplads: O(h)


