En encoder er et digitalt kredsløb, der konverterer et sæt binære input til en unik binær kode. Den binære kode repræsenterer inputtets position og bruges til at identificere den specifikke input, der er aktiv. Indkodere bruges almindeligvis i digitale systemer til at konvertere et parallelt sæt af input til en seriel kode.
Det grundlæggende princip for en encoder er at tildele en unik binær kode til hver mulig indgang. For eksempel har en 2-til-4-linjekoder 2 inputlinjer og 4 outputlinjer og tildeler en unik 4-bit binær kode til hver af de 2^2 = 4 mulige inputkombinationer. Udgangen af en koder er normalt aktiv lav, hvilket betyder, at kun én udgang er aktiv (lav) på et givet tidspunkt, og de resterende udgange er inaktive (høj). Den aktive lave udgang vælges baseret på den binære kode, der er tildelt den aktive indgang.
Der er forskellige typer indkodere, herunder prioritetsindkodere, som tildeler en prioritet til hver indgang, og binærvægtede indkodere, som bruger et binært vægtningssystem til at tildele binære koder til indgange. Sammenfattende er en encoder et digitalt kredsløb, der konverterer et sæt binære inputs til en unik binær kode, der repræsenterer inputtets position. Indkodere er meget udbredt i digitale systemer til at konvertere parallelle input til serielle koder.
En encoder er en kombinationskredsløb der udfører den omvendte operation af en Dekoder . Den har et maksimum på 2^n indgangslinjer og 'n' udgangslinjer , derfor koder den informationen fra 2^n input til en n-bit kode. Det vil producere en binær kode svarende til input, som er aktiv Høj. Derfor koder koderen 2^n inputlinjer med 'n' bits.
Encoder
Typer af kodere
Der er forskellige typer kodere, som er nævnt nedenfor.
- 4 til 2 encoder
- Oktal til binær koder (8 til 3 koder)
- Decimal til BCD Encoder
- Prioritetskoder
4 til 2 encoder
4 til 2 Encoderen består af fire indgange Y3, Y2, Y1 & Y0, og to udgange A1 & A0 . Til enhver tid kan kun én af disse 4 indgange være '1' for at få den respektive binære kode ved udgangen. Figuren nedenfor viser det logiske symbol for 4 til 2 encoderen.
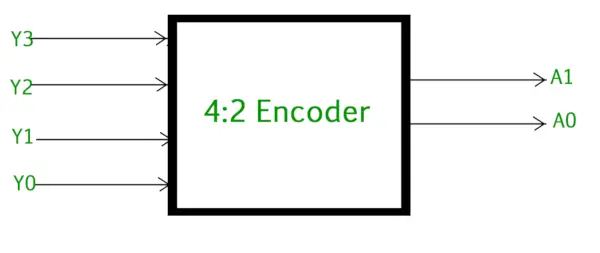
4 til 2 encoder
Sandhedstabellen med 4 til 2 indkodere er som følger.
| INDGANG | OUTPUTS | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Logisk udtryk for A1 og A0:
A1 = Y3 + Y2 A0 = Y3 + Y1>
Ovenstående to booleske funktioner A1 og A0 kan implementeres ved hjælp af to input-ELLER-gates:
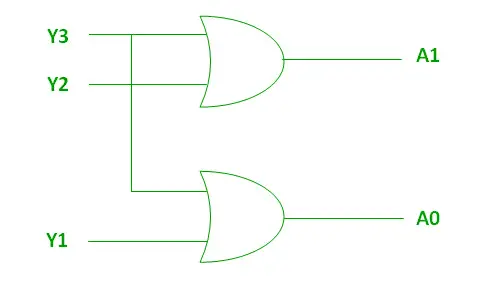
Implementering ved hjælp af OR Gate
Oktal til binær koder (8 til 3 koder)
8 til 3 encoder eller oktal til binær encoder består af 8 indgange : Y7 til Y0 og 3 udgange : A2, A1 & A0. Hver indgangslinje svarer til hvert oktal ciffer, og tre udgange genererer tilsvarende binær kode. Figuren nedenfor viser det logiske symbol for oktal til den binære encoder.
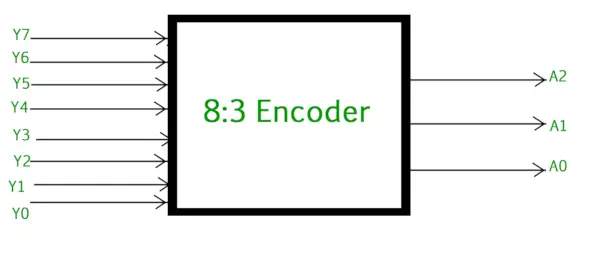
Oktal til binær koder (8 til 3 koder)
Sandhedstabellen for 8 til 3 encoderen er som følger.
| INDGANG | OUTPUTS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Logisk udtryk for A2, A1 og A0.
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
Ovenstående to booleske funktioner A2, A1 og A0 kan implementeres ved hjælp af fire input ELLER porte .
hvordan man opdaterer i java
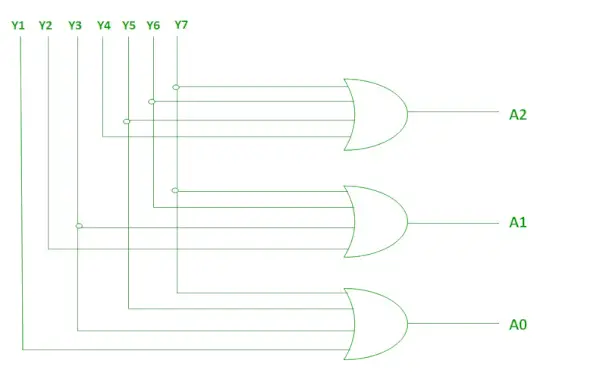
Implementering ved hjælp af OR Gate
Decimal til BCD Encoder
Den decimal-til-binære encoder består normalt af 10 input linjer og 4 udgangslinjer . Hver inputlinje svarer til hvert decimaltal, og 4 udgange svarer til BCD-koden. Denne encoder accepterer de afkodede decimaldata som input og koder dem til BCD-outputtet, som er tilgængeligt på outputlinjerne. Figuren nedenfor viser det logiske symbol for decimal til BCD-koderen:
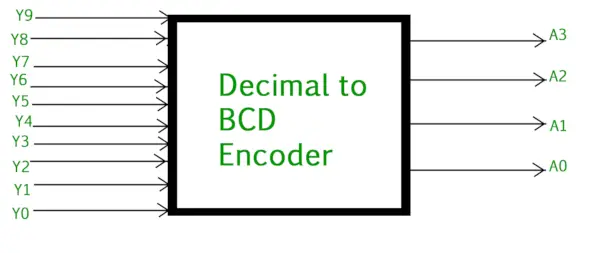
Decimal til BCD Encoder
Sandhedstabellen for decimal til BCD encoder er som følgende.
| INDGANG | OUTPUTS | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | Y8 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Logisk udtryk for A3, A2, A1 og A0.
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
Ovenstående to booleske funktioner kan implementeres ved hjælp af OR-gates.
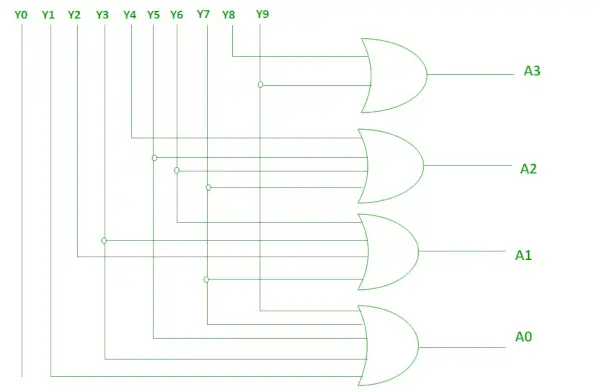
Implementering ved hjælp af OR Gate
Prioritetskoder
En 4 til 2 prioritet encoder har 4 indgange : Y3, Y2, Y1 & Y0 og 2 udgange : A1 & A0. Her har input, Y3 højeste prioritet , hvorimod input Y0 har laveste prioritet . I dette tilfælde, selvom mere end én indgang er '1' på samme tid, vil outputtet være den (binære) kode, der svarer til inputtet, som har højere prioritet . Sandhedstabellen for prioritetskoderen er som følger.
| INDGANGE | OUTPUTS | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | I |
| 0 | 0 | 0 | 0 | x | x | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | x | x | 1 | 0 | 1 |
| 1 | x | x | x | 1 | 1 | 1 |
Det logiske udtryk for A1 er vist nedenfor.
centos vs rhel
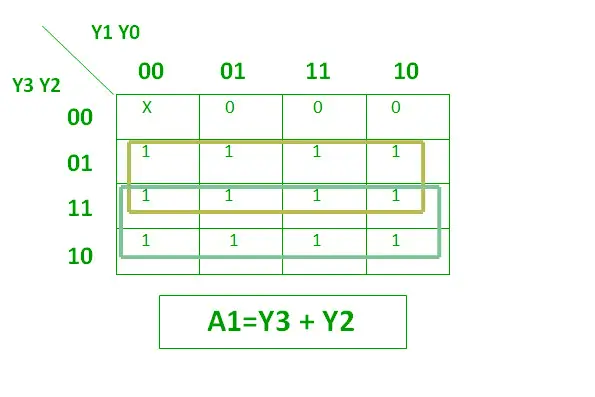
Logisk udtryk
Det logiske udtryk for A0 er vist nedenfor.
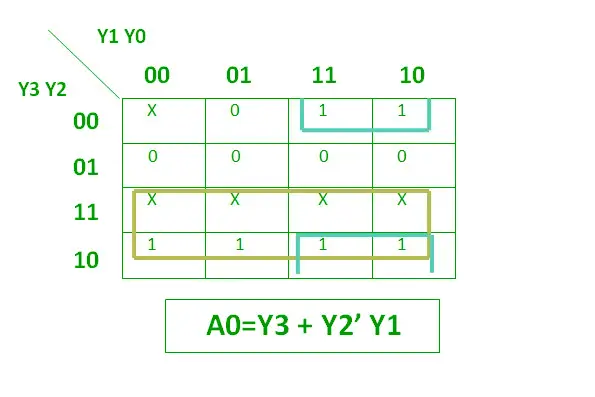
Logisk udtryk
Ovenstående to booleske funktioner kan implementeres som.
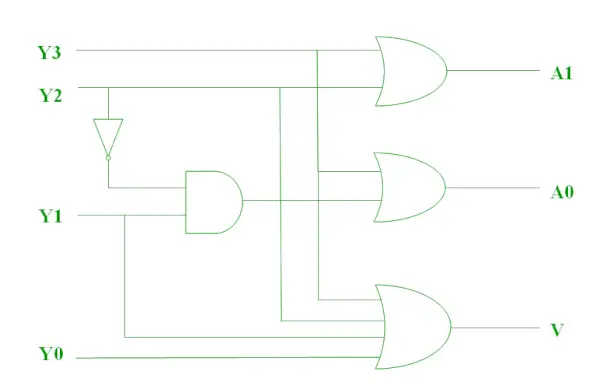
Prioritetskoder
Der er nogle fejl, der normalt opstår i Encodere er nævnt nedenfor.
- Der er en tvetydighed, når alle udgange fra koderen er lig med nul.
- Hvis mere end én indgang er aktiv Høj, producerer encoderen et output, som muligvis ikke er den korrekte kode.
Så for at overvinde disse vanskeligheder bør vi tildele prioriteter til hver indgang af encoderen. Derefter vil koderens output være den kode, der svarer til de aktive høje input, som har højere prioritet.
Anvendelse af kodere
- Encodere er meget almindelige elektroniske kredsløb, der bruges i alle digitale systemer.
- Indkodere bruges til at oversætte decimalværdierne til det binære for at udføre binære funktioner såsom addition, subtraktion, multiplikation osv.
- Andre applikationer specielt til Priority Encodere kan omfatte detektering af afbrydelser i mikroprocessorapplikationer.
Fordele ved at bruge kodere i digital logik
- Reduktion i antallet af linjer: Indkodere reducerer antallet af linjer, der kræves for at overføre information fra flere input til en enkelt output, hvilket kan forenkle systemets design og reducere omkostningerne til komponenter.
- Forbedret pålidelighed: Ved at konvertere flere input til en enkelt seriel kode kan indkodere reducere muligheden for fejl i transmissionen af information.
- Forbedret ydeevne: Indkodere kan forbedre ydeevnen af et digitalt system ved at reducere den tid, der kræves til at overføre information fra flere input til en enkelt output.
Ulemper ved at bruge kodere i digital logik
- Øget kompleksitet: Indkodere er typisk mere komplekse kredsløb sammenlignet med multipleksere , og kræver yderligere komponenter at implementere.
- Begrænset til specifikke applikationer: Encodere er kun egnet til applikationer, hvor et parallelt sæt indgange skal konverteres til en seriel kode.
- Begrænset fleksibilitet: Indkodere er begrænset i deres fleksibilitet, da de kun kan kode et fast antal indgange til et fast antal udgange.
- Afslutningsvis er indkodere nyttige digitale kredsløb, der har deres fordele og ulemper. Valget af, om der skal bruges en encoder eller ej, afhænger af de specifikke krav til systemet og afvejningen mellem kompleksitet, pålidelighed, ydeevne og omkostninger.
GATE CS hjørnespørgsmål
Øvelse af følgende spørgsmål vil hjælpe dig med at teste din viden. Alle spørgsmål er blevet stillet i GATE i tidligere år eller i GATE Mock Tests. Det anbefales stærkt, at du praktiserer dem.
- GATE CS 2013, spørgsmål 65
- GATE CS 2014 (sæt 3), spørgsmål 65
