I denne artikel vil vi gennemgå multiplekseren, vi vil først definere, hvad der er en multiplekser, derefter vil vi gennemgå dens typer, som er 2×1 og 4×1, derefter vil vi gennemgå implementeringen af ​​2×1 mux og højere mux med lavere orden mux, Til sidst vil vi afslutte vores artikel med nogle applikationer, fordele og nogle ofte stillede spørgsmål.

Indholdsfortegnelse

• Hvad er multipleksere?
• Typer af Mux
• 2×1 multiplekser
• 4×1 multiplexer
• Implementering af forskellige porte med 2:1 Mux
• Implementering af Higher Order MUX ved hjælp af Lower Order MUX
• Fordele og ulemper ved MUX

Hvad er multipleksere?

En multiplekser er en kombinationskredsløb der har mange dataindgange og en enkelt udgang, afhængigt af kontrol eller udvalgte input. For N inputlinjer kræves log2(N)-selektionslinjer eller tilsvarende for2^ninput linjer, n markeringslinjer er nødvendige. Multipleksere er også kendt som N-til-1-selektorer, parallel-til-seriel-omformere, mange-til-en-kredsløb og universelle logiske kredsløb. De bruges hovedsageligt til at øge mængden af ​​data, der kan sendes over et netværk inden for en vis tid og båndbredde .

Multiplexer

Typer af Mux

Mux kan være af forskellige typer baseret på input, men i denne artikel vil vi gennemgå to hovedtyper af mux, som er

• 2×1 Mux
• 4×1 Mux
  

2×1 multiplekser

2×1 er et grundlæggende kredsløb, som også er kendt 2-til-1 multiplexer, der bruges til at vælge en signal fra to indgange og overfører det til udgangen. 2×1 mux har to input-linjer, en output-linje og en enkelt markeringslinje. Den har forskellige applikationer i digitale systemer, såsom i mikroprocessor, den bruges til at vælge mellem to forskellige datakilder eller mellem to forskellige instruktioner.

Blokdiagram af 2:1 multiplexer med sandhedstabel

Nedenfor er blokdiagrammet og sandhedstabellen over 2:1 Mux. I dette blokdiagram, hvor I0 og I1 er indgangslinjerne, Y er udgangslinjen og S0 er en enkelt valglinje.

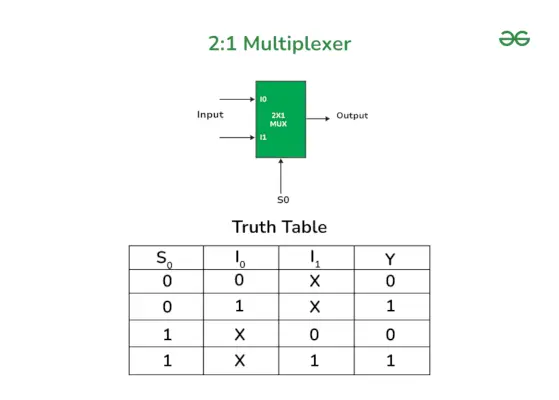
Blokdiagram af 2:1 multiplexer med sandhedstabel

Outputtet af 2×1 Mux vil afhænge af valglinjen S0,

• Når S er 0 (lav), vælges I0
• når S0 er 1(Høj), er I1 valgt

Logisk udtryk for 2×1 Mux

Ved hjælp af sandhedstabellen kan det logiske udtryk for Mux bestemmes som

Y=overline{S_0}.I_0+S_0.I_1

Kredsdiagram af 2×1 multipleksere

Brug af sandhedstabellen kredsløb diagram kan gives som

Kredsdiagram af 2×1 Mux

4×1 multiplexer

4×1 multiplekseren, som også er kendt som 4-til-1 multiplekseren. Det er en multiplexer, der har 4 indgange og en enkelt udgang. Udgangen vælges som en af ​​de 4 indgange, som er baseret på valgindgangene. Antallet af udvælgelseslinjer vil afhænge af antallet af input, som bestemmes af ligningenlog_2n,I 4×1 Mux kan udvælgelseslinjerne bestemmes somlog_4=2,slo to valg er nødvendige.

Blokdiagram af 4×1 multiplexer

I det givne blokdiagram er I0, I1, I2 og I3 de 4 indgange, og Y er Single-output, som er baseret på Select-linjer S0 og S1.

Multiplexerens output bestemmes af den binære værdi af udvælgelseslinjerne

• Når S1S0=00, vælges indgangen I0.
• Når S1S0=01, vælges indgangen I1.
• Når S1S0=10, vælges indgangen I2.
• Når S1S0=11, vælges indgangen I3.

Sandhedstabel af 4×1 multiplexer

Givet nedenfor er Sandhedstabel af 4×1 multiplexer

10 af 100,00

Kredsløbsdiagram af 4×1 multipleksere

Ved hjælp af sandhedstabel kan kredsløbsdiagrammet gives som

Multiplexer kan fungere som universelt kombinationskredsløb. Alle standard logiske porte kan implementeres med multipleksere.

Implementering af forskellige porte med 2:1 Mux

Nedenfor er implementeringen af ​​forskellige gate ved hjælp af 2:1 Mux

Implementering af NOT gate ved hjælp af 2 : 1 Mux

Not-porten fra 2:1 Mux kan fås ved

• Tilslut indgangssignalet til en af ​​dataindgangslinjerne (I0).
• Tilslut derefter en linje (0 eller 1) til den anden datainputlinje (I1)
• Tilslut den samme indgangslinje Vælg linje S0, som er forbundet til D0.

Nedenstående er diagrammet til den logiske repræsentation af IKKE port ved hjælp af 2:1 Mux

Implementering af AND gate ved hjælp af 2 : 1 Mux

And-porten fra 2:1 Mux kan fås ved

• Tilslut indgangen Y til I1.
• Forbind indgangen X til valglinien S0.
• Tilslut en linje(0) til I0.

Nedenstående er diagrammet til den logiske repræsentation af OG port ved hjælp af 2:1 Mux

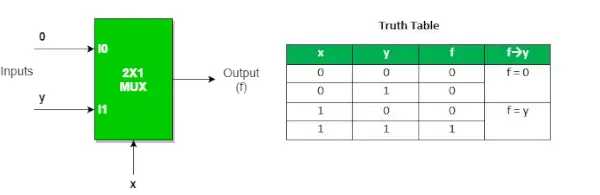
For yderligere mere om Implementering af AND gate ved hjælp af 2 : 1 Mux

Implementering af OR-port ved hjælp af 2 : 1 Mux

OR-porten fra 2:1 Mux kan fås ved

• Tilslut indgang X til valglinien S0.
• Tilslut indgang Y til I1.
• Forbind Line(1) til I1.

Nedenstående er diagrammet til den logiske repræsentation af ELLER port ved hjælp af 2:1 Mux

Implementering af NAND, NOR, XOR og XNOR porte kræver to 2:1 Mux. Første multiplekser vil fungere som IKKE-port, som vil give komplementeret input til den anden multiplekser.

Implementering af NAND-gate ved hjælp af 2 : 1 Mux

NAND-porten fra 2:1 Mux kan fås ved

• I første mux tages input og 1 og 0 og y som valglinje.
• I Second MUX er udgangen fra mux forbundet til I1.
• linje(1) er givet til I0.
• x er angivet som udvælgelseslinje for den anden Mux.

Nedenstående er diagrammet til den logiske repræsentation af NAND port ved hjælp af 2:1 Mux

For yderligere mere om Implementering af NAND-gate ved hjælp af 2 : 1 Mux

Implementering af NOR-port ved hjælp af 2 : 1 Mux

Nor-porten fra 2:1 Mux kan fås ved

java int som streng

• I første mux tages input og 1 og 0 og y som valglinje.
• I Second MUX er udgangen fra mux forbundet til I0.
• linje(0) er givet til I1.
• x er angivet som udvælgelseslinje for den anden Mux.

Nedenstående er diagrammet til den logiske repræsentation af NOR-port ved hjælp af 2:1 Mux

For yderligere mere om Implementering af NOR-port ved hjælp af 2 : 1 Mux

Implementering af EX-OR gate ved hjælp af 2 : 1 Mux

Nor-porten fra 2:1 Mux kan fås ved

• I første mux tages input og 1 og 0 og y som valglinje.
• I Second MUX er udgangen fra mux forbundet til I1.
• y gives til I0.
• x er angivet som udvælgelseslinje for den anden Mux.

Nedenstående er diagrammet til den logiske repræsentation af EX-OR port ved hjælp af 2:1 Mux

Implementering af EX-NOR gate ved hjælp af 2 : 1 Mux

Nedenstående er diagrammet til den logiske repræsentation af EX-OR port ved hjælp af 2:1 Mux

Nor-porten fra 2:1 Mux kan fås ved

• I første mux tages input og 1 og 0 og y som valglinje.
• I Second MUX er udgangen fra mux forbundet til I0.
• y gives til I1.
• x er angivet som udvælgelseslinje for den anden Mux.

Implementering af Higher Order MUX ved hjælp af Lower Order MUX

Nedenfor er implementeringen af ​​Higher Order MUX ved hjælp af Lower Order MUX

4 : 1 MUX ved hjælp af 2 : 1 MUX

Tre 2:1 MUX er nødvendige for at implementere 4:1 MUX.

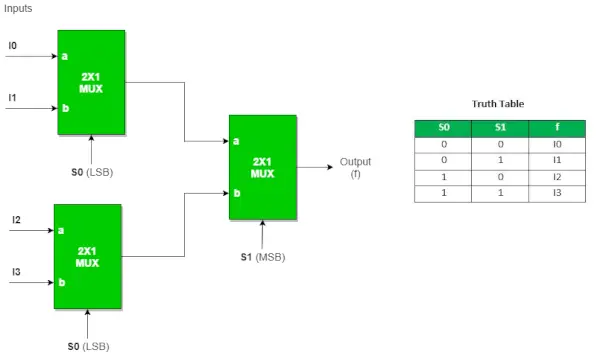
Tilsvarende

Mens en 8:1 MUX kræver syv (7) 2:1 MUX'er, kræver en 16:1 MUX femten (15) 2:1 MUX'er, og en 64:1 MUX kræver treogtres (63) 2:1 MUX'er. Derfor kan vi drage den konklusion, at en2^n:1MUX kræver(2^n-1) 2:1 MUXes.

16 : 1 MUX ved hjælp af 4 : 1 MUX

Nedenfor er det logiske diagram af 16:1 Mux ved hjælp af 4:1 Mux

Generelt, for at implementere B : 1 MUX ved hjælp af A : 1 MUX, bruges én formel til at implementere den samme.
B/A = K1,
K1/A = K2,
K2/A = K3

K_N-1/ A = K_N= 1 (indtil vi opnår 1 optælling af MUX).

Og tilføj derefter alle tallene for MUXer = K1 + K2 + K3 + …. + K_N.
At implementere 64 : 1 MUX ved hjælp af 4 : 1 MUX
Ved at bruge ovenstående formel kan vi opnå det samme.
64/4 = 16
16/4 = 4
4/4 = 1 (indtil vi opnår 1 antal MUX)
Derfor kræves et samlet antal på 4 : 1 MUX for at implementere 64 : 1 MUX = 16 + 4 + 1 = 21.

f (A, B, C) =sum( 1, 2, 3, 5, 6 ) med ligeglad (7)

ved at bruge A og B som valglinjer for 4 : 1 MUX,

AB som vælg: Udvidelse af minterms til dens booleske form og vil se dens 0 eller 1 værdi på Cth plads, så de kan placeres på den måde.

AC som vælg : Udvidelse af minterms til dens booleske form og vil se dens 0 eller 1 værdi på Bth plads, så de kan placeres på den måde.

BC som vælg : Udvidelse af minterms til sin boolske form og vil se dens 0 eller 1 værdi i A^thplaceres, så de kan placeres på den måde.

Fordele og ulemper ved MUX

Nedenfor er fordele og ulemper ved MUX

Fordele ved MUX

Nedenfor er fordelene ved MUX

• Effektivitet : Mux har god effektivitet til at dirigere flere indgangssignaler til et enkelt udsignal baseret på styresignaler.
• Optimering : Mux hjælper med at spare på ressourcer såsom ledninger, stifter og integreret kredsløb (IC).
• Forskellig implementering: Mux kan bruges til at implementere forskellige digitale logiske funktioner såsom OG,ELLER osv.
• Fleksibilitet: Mux kan nemt konfigureres i henhold til kravene og rumme forskellige datakilder, hvilket forbedrer systemets alsidighed.

Ulemper ved MUX

Nedenfor er ulemperne ved MUX

• Begrænset antal datakilder: Antallet af input, der kan tages af en multiplekser, er begrænset af antallet af kontrollinjer, hvilket kan forårsage begrænsninger i visse applikationer.
• Forsinke: Multipleksere kan have en vis forsinkelse i signalvejen, hvilket kan have indflydelse på kredsløbets ydeevne.
• Kompleks kontrolrationale: Styrelogikken for multipleksere kan være kompleks, især for større multipleksere med et stort antal input.
• Strømudnyttelse: Multiplexere kan forbruge mere strøm sammenlignet med andre simple l ogisk port , især når de har et stort antal input.

Anvendelser af MUX

Nedenfor er applikationerne af MUX

• Data Routing : Mux'en bruges til datarouting i det digitale system, hvor de vælger en af ​​de flere datalinjer og omdirigerer den til outputtet.
• Datavalg : Mux'en bruges til datavalg, hvor de vælger datakilde i henhold til udvalgslinjerne.
• Analog-til-digital konvertering : Mux bruges i ADC for at vælge forskellige analoge indgangskanaler.
• Adresseafkodning : Mux bruges i Mikroprocessorer eller hukommelse til adresseafkodning.
• Implementering af logiske funktioner : Muxes kan bruges til at implementere forskellige logiske funktioner.

Konklusion

I denne artikel har vi gennemgået MUX, vi har set Forskellige typer Mux som er 2×1 og 4×1 Mux, vi har gennemgået implementeringen af ​​2×1 mux og højere mux med lavere ordens mux. Vi har også gennemgået dets fordele, ulemper og applikationer kort.

hvad er en grænseflade

Multipleksere i digital logik – ofte stillede spørgsmål

Hvorfor anses kontrollogikken for multipleksere for kompleks?

Mux kan være kompleks, især for større multipleksere på grund af styresignalerne, som vælger input baseret på applikationskravene.

Hvad er de forskellige typer multiplexer-arkitekturer?

Mux-arkitekturer ændres på faktorer som det samlede antal input, antallet af udvalgte linjer og den logik, der bruges til inputvalg.

Hvordan bruges multipleksere digitale signalbehandlingsapplikationer (DSP)?

I DSP-applikationer bruges multipleksere til signalrouting, udvælgelse og behandling.