EN Tæller er en enhed, som gemmer (og nogle gange viser) antallet af gange, en bestemt hændelse eller proces har fundet sted, ofte i forhold til et ursignal. Tællere bruges i digital elektronik til tælleformål, de kan tælle specifikke begivenheder, der sker i kredsløbet. For eksempel, i UP-tælleren øger en tæller antallet for hver stigende flanke af uret. Ikke kun at tælle, en tæller kan følge den bestemte sekvens baseret på vores design som enhver tilfældig sekvens 0,1,3,2... .De kan også designes ved hjælp af flip flops. De bruges som frekvensdelere, hvor frekvensen af en given pulsbølgeform er opdelt. Tællere er sekventielle kredsløb, der tæller antallet af impulser, kan være enten i binær kode eller BCD-form. Hovedegenskaberne for en tæller er timing, sekventering og optælling. Tælleren fungerer i to tilstande
Op tæller
Ned tæller
Modklassifikation
Tællere er groft opdelt i to kategorier
- Asynkron tæller
- Synkrontæller
1. Asynkron tæller
I asynkron tæller bruger vi ikke universelt ur, kun det første flip-flop er drevet af hoveduret, og clock-inputtet fra resten af det følgende flip-flop er drevet af output fra tidligere flip flops. Vi kan forstå det ved at følge diagram-
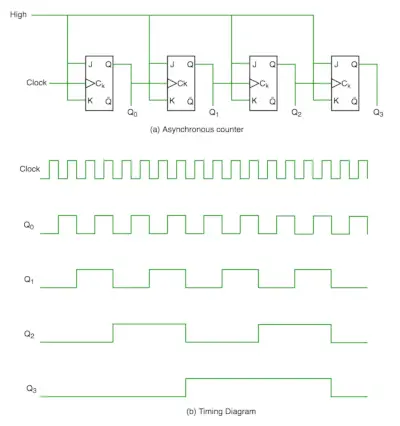
Det er tydeligt fra timingdiagrammet, at Q0 ændrer sig, så snart den stigende flanke af urimpulsen stødes på, Q1 ændres, når den stigende flanke af Q0 stødes på (fordi Q0 er som clock-impuls for anden flip flop) og så videre. På denne måde genereres ripples gennem Q0,Q1,Q2,Q3, derfor kaldes det også RIPPLE tæller og seriel tæller. En ripple-tæller er et kaskade-arrangement af flip flops, hvor outputtet fra en flip flop driver clock-indgangen på den følgende flip flop
2. Synkron tæller
I modsætning til den asynkrone tæller har den synkrone tæller et globalt ur, som driver hver flip flop, så output ændres parallelt. Den ene fordel ved synkron tæller i forhold til asynkron tæller er, at den kan fungere på højere frekvens end asynkron tæller, da den ikke har kumulativ forsinkelse på grund af samme ur, der gives til hver flip flop. Det kaldes også som paralleltæller.
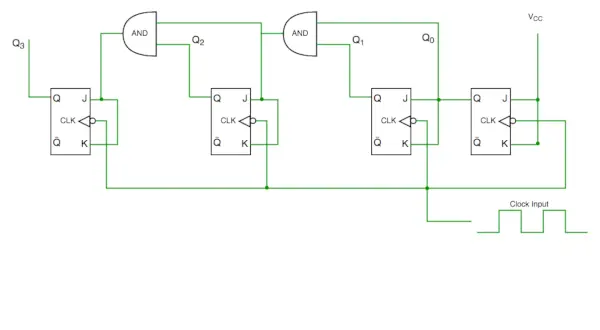
Synkront tællerkredsløb
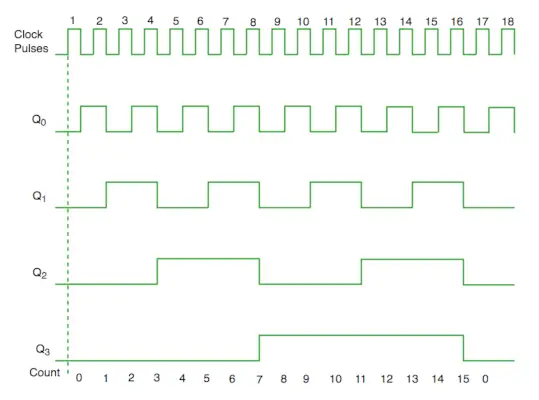
Tidsdiagram synkrontæller
Fra kredsløbsdiagram ser vi, at Q0 bit giver respons på hver faldende flanke af uret, mens Q1 er afhængig af Q0, Q2 er afhængig af Q1 og Q0, Q3 er afhængig af Q2, Q1 og Q0.
Årti tæller
En årti-tæller tæller ti forskellige tilstande og nulstilles derefter til dens oprindelige tilstande. En simpel årti-tæller vil tælle fra 0 til 9, men vi kan også lave årti-tællere, som kan gå gennem alle ti tilstande mellem 0 og 15 (for 4 bit-tællere).
| Urets puls | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Sandhedsbord til simpel årtietæller
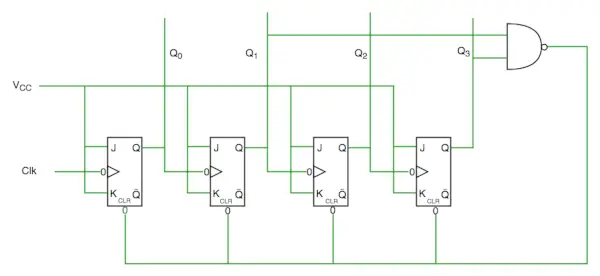
Decade tæller kredsløbsdiagram
Vi kan se fra kredsløbsdiagrammet, at vi har brugt nand-gate til Q3 og Q1 og fodret denne for at rydde indgangslinjen, fordi binær repræsentation af 10 er—
1010
Og vi ser, at Q3 og Q1 er 1 her, hvis vi giver NAND af disse to bits for at slette input, vil tælleren være klar ved 10 og igen starte fra begyndelsen.
Vigtigt punkt : Antallet af flip flops brugt i counter er altid større end lig med ( log2n ) hvor n=antal tilstande i tæller.
Nogle tidligere års portspørgsmål om tællere
Q1. Overvej den delvise implementering af en 2-bit tæller ved hjælp af T flip-flops efter sekvensen 0-2-3-1-0, som vist nedenfor
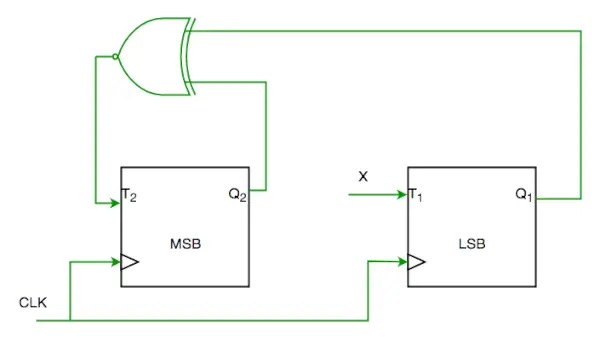
For at fuldføre kredsløbet skal indgangen X være
(A) Q2?
(B) Q2 + Q1
(C) (Q1? Q2)'
(D) Q1? Q2 (GATE-CS-2004)
Løsning:
Fra kredsløb ser vi
T1=XQ1'+X'Q1—-(1)
OG
T2=(Q2 ? Q1)'—-(2)
OG ØNSKET OUTPUT ER 00->10->11->01->00
SÅ BØR X VÆRE Q1Q2'+Q1'Q2 TILFREDSHED 1 OG 2.
SÅ ANS ER (D) DEL.
Q2. Styresignalfunktionerne for en 4-bit binær tæller er angivet nedenfor (hvor X er ligeglad)
Tælleren er tilsluttet som følger:
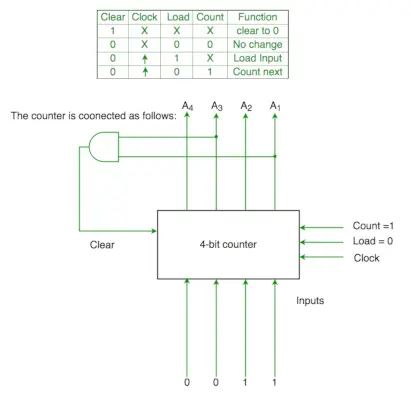
Antag, at tæller- og gateforsinkelserne er ubetydelige. Hvis tælleren starter ved 0, så cykler den gennem følgende sekvens:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (GATE-CS-2007)
Løsning:
Indledningsvis A1 A2 A3 A4 =0000
Clr=A1 og A3
Så når A1 og A3 begge er 1, går det igen til 0000
Derfor 0000(init.) -> 0001(A1 og A3=0)->0010 (A1 og A3=0) -> 0011(A1 og A3=0) -> 0100 ( A1 og A3=1 )[ klar tilstand opfyldt] ->0000(init.), så den går gennem 0->1->2->3->4
Ans er (C) del.
windows kommando arp
Quiz om digital logik
Artikel bidraget af Anuj Batham,
