Siden opfindelsen af ​​computere har folk brugt udtrykket ' Data ' for at henvise til computeroplysninger, enten transmitteret eller gemt. Der er dog data, der også findes i ordretyper. Data kan være tal eller tekster skrevet på et stykke papir i form af bits og bytes gemt i elektroniske enheders hukommelse, eller fakta gemt i en persons sind. Efterhånden som verden begyndte at modernisere sig, blev disse data et væsentligt aspekt af alles daglige liv, og forskellige implementeringer gjorde det muligt for dem at gemme dem anderledes.

Data er en samling af fakta og tal eller et sæt værdier eller værdier af et specifikt format, der refererer til et enkelt sæt af elementværdier. Dataelementerne klassificeres derefter i underelementer, som er gruppen af ​​elementer, der ikke er kendt som elementets simple primære form.

Lad os overveje et eksempel, hvor et medarbejdernavn kan opdeles i tre underpunkter: Første, Mellem og Sidste. Et ID, der er tildelt en medarbejder, vil dog generelt blive betragtet som en enkelt vare.

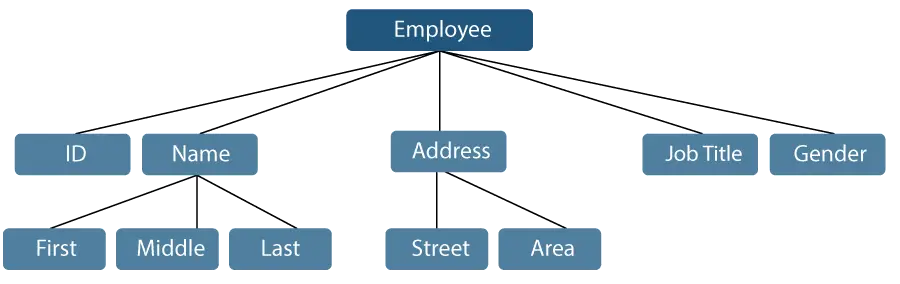
Figur 1: Repræsentation af dataelementer

I eksemplet nævnt ovenfor er elementerne såsom ID, Alder, Køn, First, Middle, Last, Street, Locality osv. elementære dataelementer. I modsætning hertil er navnet og adressen gruppedataelementer.

Hvad er datastruktur?

Datastruktur er en gren af ​​datalogi. Studiet af datastruktur giver os mulighed for at forstå organiseringen af ​​data og styringen af ​​datastrømmen for at øge effektiviteten af ​​enhver proces eller program. Datastruktur er en særlig måde at gemme og organisere data på i computerens hukommelse, så disse data nemt kan hentes og effektivt udnyttes i fremtiden, når det er nødvendigt. Dataene kan styres på forskellige måder, ligesom den logiske eller matematiske model for en specifik organisering af data er kendt som en datastruktur.

Omfanget af en bestemt datamodel afhænger af to faktorer:

1. For det første skal det indlæses nok i strukturen til at afspejle den definitive korrelation af dataene med et objekt i den virkelige verden.
2. For det andet skal dannelsen være så ligetil, at man kan tilpasse sig til at behandle dataene effektivt, når det er nødvendigt.

Nogle eksempler på datastrukturer er arrays, linkede lister, stak, kø, træer osv. Datastrukturer er meget udbredt i næsten alle aspekter af datalogi, dvs. compilerdesign, operativsystemer, grafik, kunstig intelligens og mange flere.

Datastrukturer er hoveddelen af ​​mange computervidenskabelige algoritmer, da de giver programmørerne mulighed for at administrere dataene på en effektiv måde. Det spiller en afgørende rolle i at forbedre ydeevnen af ​​et program eller software, da hovedformålet med softwaren er at gemme og hente brugerens data så hurtigt som muligt.

sortere et array java

Grundlæggende terminologier relateret til datastrukturer

Datastrukturer er byggestenene i enhver software eller ethvert program. At vælge den passende datastruktur til et program er en ekstremt udfordrende opgave for en programmør.

Følgende er nogle grundlæggende terminologier, der bruges, når datastrukturerne er involveret:

Data:Vi kan definere data som en elementær værdi eller en samling af værdier. For eksempel er medarbejderens navn og ID de data, der er relateret til medarbejderen.Dataelementer:En enkelt værdienhed er kendt som dataelement.Gruppeartikler:Dataelementer, der har underordnede dataelementer, er kendt som gruppeelementer. For eksempel kan en medarbejders navn have et for-, mellem- og efternavn.Elementære varer:Dataelementer, der ikke kan opdeles i underelementer, kaldes elementære elementer. For eksempel ID på en medarbejder.Enhed og attribut:En klasse af bestemte objekter er repræsenteret af en Entitet. Den består af forskellige attributter. Hver egenskab symboliserer den pågældende enheds specifikke egenskab. For eksempel,

Enheder med lignende attributter danner en Entitetssæt . Hver attribut i et enhedssæt har en række værdier, sættet af alle mulige værdier, der kunne tildeles den specifikke attribut.

Udtrykket 'information' bruges nogle gange om data med givne attributter af meningsfulde eller behandlede data.

Mark:En enkelt elementær informationsenhed, der symboliserer en enheds attribut, er kendt som felt.Optage:En samling af forskellige dataelementer er kendt som en post. For eksempel, hvis vi taler om medarbejderenheden, så kan dens navn, id, adresse og jobtitel grupperes for at danne posten for medarbejderen.Fil:En samling af forskellige poster af en enhedstype er kendt som en fil. For eksempel, hvis der er 100 medarbejdere, vil der være 25 poster i den relaterede fil, der indeholder data om hver medarbejder.

Forstå behovet for datastrukturer

Efterhånden som applikationer bliver mere komplekse, og mængden af ​​data stiger hver dag, hvilket kan føre til problemer med datasøgning, behandlingshastighed, håndtering af flere anmodninger og mange flere. Datastrukturer understøtter forskellige metoder til at organisere, administrere og gemme data effektivt. Ved hjælp af Data Structures kan vi nemt krydse dataelementerne. Datastrukturer giver effektivitet, genanvendelighed og abstraktion.

Hvorfor skal vi lære datastrukturer?

1. Datastrukturer og algoritmer er to af nøgleaspekterne ved datalogi.
2. Datastrukturer giver os mulighed for at organisere og gemme data, hvorimod algoritmer giver os mulighed for at behandle disse data meningsfuldt.
3. At lære datastrukturer og algoritmer vil hjælpe os med at blive bedre programmører.
4. Vi vil være i stand til at skrive kode, der er mere effektiv og pålidelig.
5. Vi vil også være i stand til at løse problemer hurtigere og mere effektivt.

Forståelse af målene for datastrukturer

Datastrukturer opfylder to komplementære mål:

Rigtighed:Datastrukturer er designet til at fungere korrekt for alle former for input baseret på interessedomænet. Med ord, korrekthed udgør det primære mål for datastrukturen, som altid afhænger af de problemer, som datastrukturen er beregnet til at løse.Effektivitet:Datastrukturer kræver også at være effektive. Det bør behandle dataene hurtigt uden at bruge mange computerressourcer som hukommelsesplads. I en realtidstilstand er effektiviteten af ​​en datastruktur en nøglefaktor for at bestemme processens succes og fiasko.

Forstå nogle nøglefunktioner i datastrukturer

Nogle af de væsentlige egenskaber ved datastrukturer er:

Robusthed:Generelt sigter alle computerprogrammører på at producere software, der giver korrekt output for alle mulige input, sammen med effektiv udførelse på alle hardwareplatforme. Denne type robust software skal håndtere både gyldige og ugyldige input.Tilpasningsevne:Opbygning af softwareapplikationer som webbrowsere, tekstbehandlere og internetsøgemaskine omfatter enorme softwaresystemer, der kræver korrekt og effektiv drift eller udførelse i mange år. Desuden udvikler software sig på grund af nye teknologier eller stadigt skiftende markedsforhold.Genanvendelighed:Funktioner som genbrug og tilpasningsevne går hånd i hånd. Det er kendt, at programmøren har brug for mange ressourcer til at bygge enhver software, hvilket gør det til en dyr virksomhed. Men hvis softwaren er udviklet på en genanvendelig og tilpasningsdygtig måde, så kan den anvendes i de fleste fremtidige applikationer. Ved at eksekvere kvalitetsdatastrukturer er det således muligt at bygge genanvendelig software, som ser ud til at være omkostningseffektiv og tidsbesparende.

Klassificering af datastrukturer

En datastruktur leverer et struktureret sæt variabler relateret til hinanden på forskellige måder. Det danner grundlaget for et programmeringsværktøj, der angiver forholdet mellem dataelementerne og giver programmører mulighed for at behandle dataene effektivt.

Vi kan klassificere datastrukturer i to kategorier:

1. Primitiv datastruktur
2. Ikke-primitiv datastruktur

Den følgende figur viser de forskellige klassifikationer af datastrukturer.

Figur 2: Klassifikationer af datastrukturer

Primitive datastrukturer

Primitive datastrukturerer datastrukturerne, der består af tallene og de tegn, der kommer indbygget ind i programmer.
1. Disse datastrukturer kan manipuleres eller betjenes direkte af instruktioner på maskinniveau.
2. Grundlæggende datatyper som Heltal, flydende, tegn , og Boolean kommer ind under de primitive datastrukturer.
3. Disse datatyper kaldes også Simple datatyper , da de indeholder tegn, der ikke kan opdeles yderligere

Ikke-primitive datastrukturer

Ikke-primitive datastrukturerer de datastrukturer, der er afledt af Primitive Data Structures.
1. Disse datastrukturer kan ikke manipuleres eller betjenes direkte af instruktioner på maskinniveau.
2. Fokus for disse datastrukturer er at danne et sæt af dataelementer, der er enten homogen (samme datatype) eller heterogen (forskellige datatyper).
3. Baseret på strukturen og arrangementet af data kan vi opdele disse datastrukturer i to underkategorier -
   1. Lineære datastrukturer
   2. Ikke-lineære datastrukturer

Lineære datastrukturer

En datastruktur, der bevarer en lineær forbindelse mellem sine dataelementer, er kendt som en lineær datastruktur. Ordningen af ​​dataene udføres lineært, hvor hvert element består af efterfølgere og forgængere undtagen det første og det sidste dataelement. Det er dog ikke nødvendigvis sandt i tilfælde af hukommelse, da arrangementet muligvis ikke er sekventielt.

Baseret på hukommelsesallokering er de lineære datastrukturer yderligere klassificeret i to typer:

Statiske datastrukturer:Datastrukturerne med en fast størrelse er kendt som statiske datastrukturer. Hukommelsen til disse datastrukturer allokeres på kompileringstidspunktet, og deres størrelse kan ikke ændres af brugeren efter kompilering; dog kan de lagrede data i dem ændres.
Det Array er det bedste eksempel på den statiske datastruktur, da de har en fast størrelse, og dens data kan ændres senere.Dynamiske datastrukturer:Datastrukturerne med en dynamisk størrelse er kendt som dynamiske datastrukturer. Hukommelsen af ​​disse datastrukturer tildeles ved kørselstiden, og deres størrelse varierer i løbet af kodens kørselstid. Desuden kan brugeren ændre størrelsen samt de dataelementer, der er gemt i disse datastrukturer, når koden køres.
Sammenkædede lister, stakke , og Haler er almindelige eksempler på dynamiske datastrukturer

Typer af lineære datastrukturer

Følgende er listen over lineære datastrukturer, som vi generelt bruger:

linux kommandoer hvilke

1. Arrays

An Array er en datastruktur, der bruges til at indsamle flere dataelementer af samme datatype i én variabel. I stedet for at gemme flere værdier af de samme datatyper i separate variabelnavne, kunne vi gemme dem alle sammen i én variabel. Denne erklæring indebærer ikke, at vi bliver nødt til at forene alle værdierne af den samme datatype i et hvilket som helst program i et array af den datatype. Men der vil ofte være tidspunkter, hvor nogle specifikke variabler af de samme datatyper alle er relateret til hinanden på en måde, der passer til et array.

Et array er en liste over elementer, hvor hvert element har en unik plads på listen. Dataelementerne i arrayet deler det samme variabelnavn; hver bærer dog et forskelligt indeksnummer kaldet et subscript. Vi kan få adgang til ethvert dataelement fra listen ved hjælp af dets placering på listen. Det vigtigste træk ved arrays at forstå er således, at dataene er lagret i sammenhængende hukommelsesplaceringer, hvilket gør det muligt for brugerne at krydse dataelementerne i arrayet ved hjælp af deres respektive indekser.

Figur 3. En Array

Arrays kan klassificeres i forskellige typer:

One-Dimensional Array:Et array med kun én række af dataelementer er kendt som et One-Dimensional Array. Den opbevares i stigende lagerplads.Todimensionelt array:Et array, der består af flere rækker og kolonner af dataelementer, kaldes et todimensionelt array. Det er også kendt som en Matrix.Multidimensionelt array:Vi kan definere Multidimensional Array som en Array af Arrays. Multidimensionelle arrays er ikke afgrænset til to indekser eller to dimensioner, da de kan omfatte så mange indekser, der passer til behovet.

Nogle applikationer af Array:

1. Vi kan gemme en liste over dataelementer, der tilhører samme datatype.
2. Array fungerer som et hjælpelager for andre datastrukturer.
3. Arrayet hjælper også med at lagre dataelementer i et binært træ med det faste antal.
4. Array fungerer også som et lager af matricer.

2. Sammenkædede lister

EN Linket liste er et andet eksempel på en lineær datastruktur, der bruges til at lagre en samling af dataelementer dynamisk. Dataelementer i denne datastruktur er repræsenteret af noderne, forbundet med links eller pointere. Hver node indeholder to felter, informationsfeltet består af de faktiske data, og pointerfeltet består af adressen på de efterfølgende noder i listen. Pointeren på den sidste knude på den sammenkædede liste består af en nul-markør, da den ikke peger på noget. I modsætning til arrays kan brugeren dynamisk justere størrelsen på en linket liste i henhold til kravene.

Figur 4. En sammenkædet liste

Linkede lister kan klassificeres i forskellige typer:

Enkelt linket liste:En enkelt linket liste er den mest almindelige type linked liste. Hver knude har data og et markørfelt, der indeholder en adresse til den næste knude.Dobbelt linket liste:En dobbeltforbundet liste består af et informationsfelt og to markørfelter. Informationsfeltet indeholder dataene. Det første markørfelt indeholder en adresse på den forrige node, hvorimod et andet markørfelt indeholder en reference til den næste node. Således kan vi gå i begge retninger (bagud såvel som fremad).Cirkulær linket liste:Den cirkulære linkede liste ligner den enkeltstående liste. Den eneste nøgleforskel er, at den sidste knude indeholder adressen på den første knude, der danner en cirkulær sløjfe i den cirkulære sammenkædede liste.

Nogle applikationer af linkede lister:

1. De linkede lister hjælper os med at implementere stakke, køer, binære træer og grafer af foruddefineret størrelse.
2. Vi kan også implementere Operativsystems funktion til dynamisk hukommelseshåndtering.
3. Sammenkædede lister tillader også polynomiumimplementering til matematiske operationer.
4. Vi kan bruge Circular Linked List til at implementere operativsystemer eller applikationsfunktioner, som Round Robin udfører opgaver.
5. Cirkulær linket liste er også nyttig i et diasshow, hvor en bruger skal gå tilbage til det første dias, efter at det sidste dias er præsenteret.
6. Dobbelt linket liste bruges til at implementere frem- og tilbageknapper i en browser for at flytte frem og tilbage på de åbne sider på et websted.

3. Stabler

EN Stak er en lineær datastruktur, der følger LIFO (Last In, First Out) princip, der tillader operationer som indsættelse og sletning fra den ene ende af stakken, dvs. Top. Stabler kan implementeres ved hjælp af sammenhængende hukommelse, et array og ikke-sammenhængende hukommelse, en linket liste. Eksempler fra det virkelige liv på stakke er bunker af bøger, et sæt kort, bunker af penge og mange flere.

latex tekststørrelse

Figur 5. Et virkeligt eksempel på stak

Ovenstående figur repræsenterer det virkelige eksempel på en stak, hvor handlingerne kun udføres fra den ene ende, som f.eks. indsættelse og fjernelse af nye bøger fra toppen af ​​stakken. Det indebærer, at indsættelse og sletning i stakken kun kan udføres fra toppen af ​​stakken. Vi kan kun få adgang til stakkens toppe på ethvert givet tidspunkt.

De primære operationer i stakken er som følger:

Skubbe:Operation for at indsætte et nyt element i stakken betegnes som push-operation.Pop:Operation for at fjerne eller slette elementer fra stakken kaldes Pop Operation.

Figur 6. En stak

Nogle anvendelser af stakke:

1. Stakken bruges som en midlertidig lagerstruktur til rekursive operationer.
2. Stack bruges også som Auxiliary Storage Structure til funktionskald, indlejrede operationer og udskudte/udskudte funktioner.
3. Vi kan administrere funktionskald ved hjælp af Stacks.
4. Stabler bruges også til at evaluere de aritmetiske udtryk i forskellige programmeringssprog.
5. Stakke er også nyttige til at konvertere infix-udtryk til postfix-udtryk.
6. Stacks giver os mulighed for at kontrollere udtrykkets syntaks i programmeringsmiljøet.
7. Vi kan matche parenteser ved hjælp af stakke.
8. Stabler kan bruges til at vende en streng.
9. Stabler er nyttige til at løse problemer baseret på backtracking.
10. Vi kan bruge stakke i dybde-først søgning i graf og trægennemgang.
11. Stabler bruges også i operativsystemets funktioner.
12. Stabler bruges også i UNDO- og REDO-funktionerne i en redigering.

4. Haler

EN Kø er en lineær datastruktur, der ligner en stak med nogle begrænsninger for indsættelse og sletning af elementerne. Indsættelsen af ​​et element i en kø udføres i den ene ende, og fjernelsen sker i den anden eller modsatte ende. Således kan vi konkludere, at Queue-datastrukturen følger FIFO-princippet (First In, First Out) for at manipulere dataelementerne. Implementering af køer kan udføres ved hjælp af arrays, linkede lister eller stakke. Nogle eksempler fra det virkelige liv på køer er en kø ved billetskranken, en rulletrappe, en bilvask og mange flere.

Figur 7. Et virkeligt eksempel på kø

java hvis andet

Ovenstående billede er en virkelig illustration af en biografbilletskranke, der kan hjælpe os med at forstå køen, hvor kunden, der kommer først, altid bliver serveret først. Kunden, der ankommer sidst, vil uden tvivl blive serveret sidst. Begge ender af køen er åbne og kan udføre forskellige operationer. Et andet eksempel er en food court-linje, hvor kunden indsættes fra bagenden, mens kunden fjernes i forenden efter at have leveret den service, de bad om.

Følgende er de primære handlinger i køen:

Kø:Indsættelsen eller tilføjelsen af ​​nogle dataelementer til køen kaldes Enqueue. Elementindsættelsen sker altid ved hjælp af den bagerste viser.Afkø:Sletning eller fjernelse af dataelementer fra køen kaldes Dequeue. Sletningen af ​​elementet sker altid ved hjælp af frontmarkøren.

Figur 8. Kø

Nogle applikationer af køer:

1. Køer bruges generelt i breddesøgningsoperationen i Graphs.
2. Køer bruges også i Job Scheduler Operations of Operating Systems, såsom en tastaturbufferkø til at gemme de taster, der trykkes af brugere, og en printbufferkø til at gemme de dokumenter, der udskrives af printeren.
3. Køer er ansvarlige for CPU-planlægning, jobplanlægning og diskplanlægning.
4. Prioritetskøer bruges i fil-download-operationer i en browser.
5. Køer bruges også til at overføre data mellem perifere enheder og CPU'en.
6. Køer er også ansvarlige for at håndtere afbrydelser genereret af brugerapplikationerne til CPU'en.

Ikke-lineære datastrukturer

Ikke-lineære datastrukturer er datastrukturer, hvor dataelementerne ikke er arrangeret i sekventiel rækkefølge. Her er indsættelse og fjernelse af data ikke muligt på en lineær måde. Der eksisterer et hierarkisk forhold mellem de enkelte dataelementer.

Typer af ikke-lineære datastrukturer

Følgende er listen over ikke-lineære datastrukturer, som vi generelt bruger:

1. Træer

Et træ er en ikke-lineær datastruktur og et hierarki, der indeholder en samling af noder, således at hver node i træet gemmer en værdi og en liste over referencer til andre noder ('børnene').

Trædatastrukturen er en specialiseret metode til at arrangere og indsamle data i computeren for at blive brugt mere effektivt. Den indeholder en central node, strukturelle noder og sub-noder forbundet via kanter. Vi kan også sige, at trædatastrukturen består af rødder, grene og blade forbundet.

Figur 9. Et træ

Træer kan klassificeres i forskellige typer:

Binært træ:En trædatastruktur, hvor hver overordnet node højst kan have to børn, kaldes et binært træ.Binært søgetræ:Et binært søgetræ er en trædatastruktur, hvor vi nemt kan vedligeholde en sorteret liste over tal.AVL træ:Et AVL-træ er et selvbalancerende binært søgetræ, hvor hver node vedligeholder ekstra information kendt som en balancefaktor, hvis værdi er enten -1, 0 eller +1.B-træ:Et B-træ er en speciel type selvbalancerende binært søgetræ, hvor hver node består af flere nøgler og kan have mere end to børn.

Nogle anvendelser af træer:

1. Træer implementerer hierarkiske strukturer i computersystemer som mapper og filsystemer.
2. Træer bruges også til at implementere navigationsstrukturen på et websted.
3. Vi kan generere kode som Huffmans kode ved hjælp af træer.
4. Træer er også nyttige i beslutningstagning i spilapplikationer.
5. Træer er ansvarlige for at implementere prioritetskøer for prioritetsbaserede OS-planlægningsfunktioner.
6. Træer er også ansvarlige for at analysere udtryk og udsagn i kompilatorerne af forskellige programmeringssprog.
7. Vi kan bruge træer til at gemme datanøgler til indeksering til Database Management System (DBMS).
8. Spanning Trees giver os mulighed for at rute beslutninger i computer- og kommunikationsnetværk.
9. Træer bruges også i stifindingsalgoritmen implementeret i kunstig intelligens (AI), robotteknologi og videospilsapplikationer.

2. Grafer

En graf er et andet eksempel på en ikke-lineær datastruktur, der omfatter et begrænset antal knudepunkter eller knudepunkter og de kanter, der forbinder dem. Graferne bruges til at løse problemer i den virkelige verden, hvor de betegner problemområdet som et netværk, såsom sociale netværk, kredsløbsnetværk og telefonnetværk. For eksempel kan knudepunkterne eller hjørnerne af en graf repræsentere en enkelt bruger i et telefonnetværk, mens kanterne repræsenterer forbindelsen mellem dem via telefon.

Grafdatastrukturen, G, betragtes som en matematisk struktur bestående af et sæt hjørner, V og et sæt kanter, E som vist nedenfor:

G = (V,E)

liste java

Figur 10. En graf

Ovenstående figur repræsenterer en graf med syv hjørner A, B, C, D, E, F, G og ti kanter [A, B], [A, C], [B, C], [B, D], [B, E], [C, D], [D, E], [D, F], [E, F] og [E, G].

Afhængigt af positionen af ​​hjørnerne og kanterne kan graferne klassificeres i forskellige typer:

Nul graf:En graf med et tomt sæt kanter kaldes en nulgraf.Triviel graf:En graf med kun et toppunkt kaldes en trivial graf.Simpel graf:En graf uden selvløkker eller flere kanter er kendt som en simpel graf.Multigraf:En graf siges at være Multi, hvis den består af flere kanter, men ingen selvløkker.Pseudograf:En graf med selvløkker og flere kanter kaldes en pseudograf.Ikke-rettet graf:En graf bestående af ikke-rettede kanter er kendt som en ikke-rettet graf.Instrueret graf:En graf bestående af de rettede kanter mellem hjørnerne er kendt som en rettet graf.Forbundet graf:En graf med mindst en enkelt vej mellem hvert par af hjørner kaldes en forbundet graf.Afbrudt graf:En graf, hvor der ikke eksisterer nogen sti mellem mindst et par hjørner, kaldes en afbrudt graf.Almindelig graf:En graf, hvor alle hjørner har samme grad, kaldes en regulær graf.Komplet graf:En graf, hvor alle hjørner har en kant mellem hvert par af hjørner, er kendt som en komplet graf.Cyklusgraf:En graf siges at være en cyklus, hvis den har mindst tre spidser og kanter, der danner en cyklus.Cyklisk graf:En graf siges at være cyklisk, hvis og kun hvis der findes mindst én cyklus.Acyklisk graf:En graf med nul cyklusser kaldes en acyklisk graf.Endelig graf:En graf med et begrænset antal hjørner og kanter er kendt som en endelig graf.Uendelig graf:En graf med et uendeligt antal hjørner og kanter er kendt som en uendelig graf.Todelt graf:En graf, hvor toppunkterne kan opdeles i uafhængige mængder A og B, og alle toppunkter i mængde A kun skal forbindes med de hjørner, der er til stede i sæt B med nogle kanter, betegnes som en todelt graf.Plan graf:En graf siges at være en plan, hvis vi kan tegne den i et enkelt plan med to kanter, der skærer hinanden.Euler-graf:En graf siges at være Euler, hvis og kun hvis alle hjørnerne er lige grader.Hamiltonsk graf:En forbundet graf bestående af et Hamiltonsk kredsløb er kendt som en Hamiltonsk graf.

Nogle anvendelser af grafer:

1. Grafer hjælper os med at repræsentere ruter og netværk i transport-, rejse- og kommunikationsapplikationer.
2. Grafer bruges til at vise ruter i GPS.
3. Grafer hjælper os også med at repræsentere sammenkoblingerne i sociale netværk og andre netværksbaserede applikationer.
4. Grafer bruges i kortlægningsapplikationer.
5. Grafer er ansvarlige for repræsentationen af ​​brugerpræferencer i e-handelsapplikationer.
6. Grafer bruges også i forsyningsnetværk for at identificere de problemer, der stilles til lokale eller kommunale virksomheder.
7. Grafer hjælper også med at styre udnyttelsen og tilgængeligheden af ​​ressourcer i en organisation.
8. Grafer bruges også til at lave dokumentlinkkort over webstederne for at vise forbindelsen mellem siderne gennem hyperlinks.
9. Grafer bruges også i robotbevægelser og neurale netværk.

Grundlæggende betjening af datastrukturer

I det følgende afsnit vil vi diskutere de forskellige typer operationer, som vi kan udføre for at manipulere data i hver datastruktur:

Gennemgang:At krydse en datastruktur betyder at få adgang til hvert dataelement nøjagtigt én gang, så det kan administreres. For eksempel skal der krydses, mens navnene på alle medarbejdere i en afdeling udskrives.Søg:Søgning er en anden datastrukturoperation, som betyder at finde placeringen af ​​et eller flere dataelementer, der opfylder visse begrænsninger. Et sådant dataelement kan være til stede i det givne sæt af dataelementer. For eksempel kan vi bruge søgefunktionen til at finde navnene på alle de medarbejdere, der har mere end 5 års erfaring.Indskud:Indsættelse betyder indsættelse eller tilføjelse af nye dataelementer til samlingen. For eksempel kan vi bruge indsættelsesoperationen til at tilføje oplysninger om en ny medarbejder, som virksomheden for nylig har ansat.Sletning:Sletning betyder at fjerne eller slette et bestemt dataelement fra den givne liste over dataelementer. For eksempel kan vi bruge slettehandlingen til at slette navnet på en medarbejder, der har forladt jobbet.Sortering:Sortering betyder at arrangere dataelementerne i enten stigende eller faldende rækkefølge afhængigt af applikationstypen. For eksempel kan vi bruge sorteringsoperationen til at arrangere navnene på medarbejdere i en afdeling i alfabetisk rækkefølge eller estimere månedens tre bedste præstationer ved at arrangere medarbejdernes præstationer i faldende rækkefølge og udtrække detaljerne for de tre bedste.Fusionere:Flet betyder at kombinere dataelementer fra to sorterede lister for at danne en enkelt liste over sorterede dataelementer.Skab:Create er en operation, der bruges til at reservere hukommelse til programmets dataelementer. Vi kan udføre denne operation ved hjælp af en erklæring. Oprettelse af datastruktur kan ske enten under følgende:
1. Kompileringstid
2. Run-time
   For eksempel malloc() funktion bruges i C Language til at skabe datastruktur.
Udvælgelse:Udvælgelse betyder at vælge en bestemt data fra de tilgængelige data. Vi kan vælge enhver bestemt data ved at specificere betingelser inde i løkken.Opdatering:Opdateringsoperationen giver os mulighed for at opdatere eller ændre dataene i datastrukturen. Vi kan også opdatere bestemte data ved at specificere nogle betingelser inde i løkken, f.eks. Selection-operationen.Opdeling:Opdelingsoperationen giver os mulighed for at opdele data i forskellige underdele, hvilket reducerer den samlede procesgennemførelsestid.

Forstå den abstrakte datatype

Som pr National Institute of Standards and Technology (NIST) , en datastruktur er et arrangement af information, generelt i hukommelsen, for bedre algoritmeeffektivitet. Datastrukturer omfatter sammenkædede lister, stakke, køer, træer og ordbøger. De kan også være en teoretisk enhed, som navnet og adressen på en person.

Fra definitionen nævnt ovenfor kan vi konkludere, at operationerne i datastrukturen omfatter:

1. Et højt niveau af abstraktioner som tilføjelse eller sletning af et element fra en liste.
2. Søgning og sortering af et element på en liste.
3. Adgang til det højeste prioritetselement på en liste.

Når datastrukturen udfører sådanne operationer, er det kendt som en Abstrakt datatype (ADT) .

Vi kan definere det som et sæt af dataelementer sammen med operationerne på dataene. Udtrykket 'abstrakt' henviser til, at dataene og de grundlæggende operationer, der er defineret på dem, studeres uafhængigt af deres implementering. Det inkluderer, hvad vi kan gøre med dataene, ikke hvordan vi kan gøre det.

En ADI-implementering indeholder en lagerstruktur for at gemme dataelementerne og algoritmerne til grundlæggende drift. Alle datastrukturer, såsom en matrix, sammenkædet liste, kø, stak osv., er eksempler på ADT.

Forstå fordelene ved at bruge ADT'er

I den virkelige verden udvikler programmer sig som en konsekvens af nye begrænsninger eller krav, så ændring af et program kræver generelt en ændring i en eller flere datastrukturer. Antag for eksempel, at vi ønsker at indsætte et nyt felt i en medarbejders post for at holde styr på flere detaljer om hver medarbejder. I så fald kan vi forbedre effektiviteten af ​​programmet ved at erstatte et Array med en Linked-struktur. I en sådan situation er det uegnet at omskrive enhver procedure, der bruger den modificerede struktur. Derfor er et bedre alternativ at adskille en datastruktur fra dens implementeringsinformation. Dette er princippet bag brugen af ​​abstrakte datatyper (ADT).

Nogle anvendelser af datastrukturer

Følgende er nogle anvendelser af datastrukturer:

1. Datastrukturer hjælper med at organisere data i en computers hukommelse.
2. Datastrukturer hjælper også med at repræsentere oplysningerne i databaser.
3. Data Structures tillader implementering af algoritmer til at søge gennem data (For eksempel søgemaskine).
4. Vi kan bruge datastrukturerne til at implementere algoritmerne til at manipulere data (For eksempel tekstbehandlere).
5. Vi kan også implementere algoritmerne til at analysere data ved hjælp af Data Structures (For eksempel data miners).
6. Datastrukturer understøtter algoritmer til at generere dataene (for eksempel en tilfældig talgenerator).
7. Datastrukturer understøtter også algoritmer til at komprimere og dekomprimere dataene (for eksempel et zip-værktøj).
8. Vi kan også bruge datastrukturer til at implementere algoritmer til at kryptere og dekryptere dataene (For eksempel et sikkerhedssystem).
9. Ved hjælp af Data Structures kan vi bygge software, der kan administrere filer og mapper (For eksempel en filhåndtering).
10. Vi kan også udvikle software, der kan gengive grafik ved hjælp af Data Structures. (For eksempel en webbrowser eller 3D-gengivelsessoftware).

Bortset fra dem, som tidligere nævnt, er der mange andre applikationer af datastrukturer, der kan hjælpe os med at bygge enhver ønsket software.