Z-SCORE I STATISTIK

Z-score i statistik er et mål for, hvor mange standardafvigelser et datapunkt er fra middelværdien af en fordeling. Lad os finde z-score i statistik. En z-score på 0 indikerer, at datapunktets score er den samme som middelscore. En positiv z-score angiver, at datapunktet er over gennemsnittet, mens en negativ z-score angiver, at datapunktet er under gennemsnittet.

fibonacci-sekvens java

Formlen til at beregne en z-score er: z = (x – μ)/ p

Hvor:

x: er testværdien
m: er middelværdien
på: er standardværdien

I denne artikel vil vi diskutere følgende begreber:

Indholdsfortegnelse

Hvad er Z-Score?
Hvordan beregner man Z-score?
Karakteristika for Z-Score
Beregn outliers ved hjælp af Z-Score-værdien
Implementering af Z-Score i Python
Anvendelse af Z-Score
Z-score vs. standardafvigelse
Hvorfor kaldes Z-scores Standard Scores?

Hvad er Z-Score?

Z-scoren, også kendt som standardscoren, fortæller os afvigelsen af et datapunkt fra gennemsnittet ved at udtrykke det i form af standardafvigelser over eller under middelværdien. Det giver os en idé om, hvor langt et datapunkt er fra middelværdien. Derfor måles Z-score i form af standardafvigelse fra middelværdien. For eksempel angiver en Z-score på 2, at værdien er 2 standardafvigelser væk fra middelværdien. For at bruge en z-score skal vi kende populationsmiddelværdien (μ) og også populationens standardafvigelse (σ).

Formlen for Z-Score

En z-score kan beregnes ved hjælp af følgende formel.

z = (X – μ) / p

hvor,

z = Z-score
X = Værdi af element
μ = Befolkningsmiddel
σ = Populationsstandardafvigelse

Hvordan beregner man Z-score?

Vi får givet populationsmiddelværdien (μ), populationens standardafvigelse (σ) og den observerede værdi (x) i problemformuleringen, der erstatter det samme i Z-score-ligningen, giver os Z-score-værdien. Afhængigt af om den givne Z-Score er positiv eller negativ, kan vi bruge positiv Z-tabel eller negativ Z-tabel tilgængelig online eller på bagsiden af din statistik lærebog i bilaget.

Eksempel 1:

Du tager GATE-eksamenen og scorer 500. Den gennemsnitlige score for GATE er 390 og standardafvigelsen er 45. Hvor godt scorede du på testen sammenlignet med den gennemsnitlige testdeltager?

Løsning:

Følgende data er let tilgængelige i ovenstående spørgsmål

Rå score/observeret værdi = X = 500

Gennemsnitlig score = μ = 390

Standardafvigelse = σ = 45

java pause

Ved at anvende formlen for z-score,

z = (X – μ) / p

z = (500 – 390) / 45

z = 110 / 45 = 2,44

Det betyder, at din z-score er 2,44 .

Da Z-score er positiv 2,44, vil vi gøre brug af den positive Z-tabel.

Lad os nu tage et kig på Z tabel (CC-BY) for at vide, hvor godt du scorede i forhold til de andre testpersoner.

Følg vejledningen nedenfor for at finde sandsynligheden fra tabellen.

Her, z-score = 2,44, hvilken jeg angiver, at datapunktet er 2,44 standardafvigelser over middelværdien.

Først skal du kortlægge de to første cifre 2.4 på Y-aksen.
Derefter langs X-aksen, kort 0,04
Forbind begge akser. Skæringspunktet mellem de to vil give dig den kumulative sandsynlighed forbundet med den Z-score værdi, du leder efter

[Denne sandsynlighed repræsenterer arealet under standard normalkurven til venstre for Z-score]

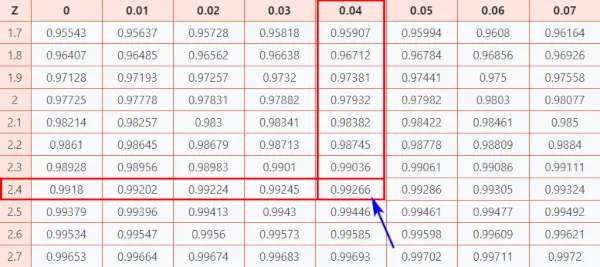
Normalfordelingstabel

Som et resultat vil du få den endelige værdi, som er 0,99266 .

Nu skal vi sammenligne, hvordan vores oprindelige score på 500 på GATE-eksamenen sammenligner med den gennemsnitlige score for partiet. For at gøre det skal vi konvertere den kumulative sandsynlighed forbundet med Z-score til en procentværdi.

0,99266 × 100 = 99,266 %

Endelig kan man sige, at man har præsteret godt end næsten 99 % af andre testpersoner.

Eksempel 2 : Hvad er sandsynligheden for, at en elev scorer mellem 350 og 400 (med en gennemsnitlig score μ på 390 og en standardafvigelse σ på 45)?

Løsning:

Min score = X₁= 350

Max score = X₂= 400

Ved at anvende formlen for z-score,

Med₁= (X1 – m) / s

Med₁= (350 – 390) / 45
java til pause

Med₁= -40 / 45 = -0,88

Med₂= (X₂– m) / s

z2 = (400 – 390) / 45

Med₂= 10/45 = 0,22

Da z1 er negativ, bliver vi nødt til at se på en negativ Z-Tabel og find ud af, at kumulativ sandsynlighed p1, den første sandsynlighed, er 0,18943 .

Med₂er positiv, så vi bruger en positiv Z-tabel, som giver en kumulativ sandsynlighed p₂af 0,58706 .

Den endelige sandsynlighed beregnes ved at trække p1 fra p₂:

p = p₂– s₁

p = 0,58706 – 0,18943 = 0,39763

Sandsynligheden for, at en elev scorer mellem 350 og 400 er 39,763 % (0,39763 * 100).

Karakteristika for Z-Score

Størrelsen af Z-scoren afspejler, hvor langt et datapunkt er fra gennemsnittet i form af standardafvigelser.
Et element med en z-score på mindre end 0 repræsenterer, at elementet er mindre end middelværdien.
Z-score giver mulighed for sammenligning af datapunkter fra forskellige distributioner.
Et element med en z-score større end 0 repræsenterer, at elementet er større end middelværdien.
Et element med en z-score lig med 0 repræsenterer, at elementet er lig med middelværdien.
Et element med en z-score lig med 1 repræsenterer, at elementet er 1 standardafvigelse større end middelværdien; en z-score lig med 2, 2 standardafvigelser større end middelværdien og så videre.
Et element med en z-score lig med -1 repræsenterer, at elementet er 1 standardafvigelse mindre end middelværdien; en z-score lig med -2, 2 standardafvigelser mindre end middelværdien og så videre.
Hvis antallet af elementer i et givet sæt er stort, så har omkring 68% af elementerne en z-score mellem -1 og 1; ca. 95 % har en z-score mellem -2 og 2; omkring 99 % har en z-score mellem -3 og 3. Dette er kendt som den empiriske regel, og den angiver procentdelen af data inden for visse standardafvigelser fra gennemsnittet i en normalfordeling som vist på billedet nedenfor

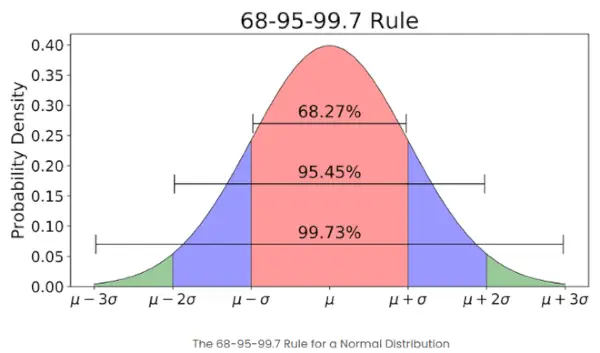
Den empiriske regel i Normalfordeling

ascii tabel java

Beregn outliers ved hjælp af Z-Score-værdien

Vi kan beregne outliers i dataene ved hjælp af z-score værdien af datapunkterne. Trinene til at overveje et afvigende datapunkt er som:

I første omgang samler vi det datasæt, som vi ønsker at se outliers i
Vi vil beregne middelværdien og standardafvigelsen for datasættet. Disse værdier vil blive brugt til at beregne z-scoreværdien for hvert datapunkt.
Vi vil beregne z-scoreværdien for hvert datapunkt. Formlen til beregning af z-scoreværdien vil være den samme som
Z = frac{{X – mu}}{{sigma}}
hvor X vil være datapunktet, μ er middelværdien af dataene, og σ er standardafvigelsen for datasættet.
Vi vil bestemme cutoff-værdien for z-score, hvorefter datapunktet kan betragtes som en outlier. Denne afskæringsværdi er en hyperparameter, som vi beslutter afhængigt af vores projekt.
Et datapunkt, hvis z-score-værdi er større end 3, betyder, at datapunktet ikke hører til 99,73 %-punktet af datasættet.
Ethvert datapunkt, hvis z-score er større end vores besluttede cutoff-værdi, vil blive betragtet som en outlier.

Kontrollere: Z-score for Outlier Detection

Implementering af Z-Score i Python

Vi kan bruge Python til at beregne z-score værdien af datapunkter i datasættet. Vi vil også bruge numpy-biblioteket til at beregne gennemsnit og standardafvigelse af datasættet.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Overvigelserne i datasættet er {outliers}')>

Produktion:

Z-score : [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Outlierne i datasættet er [150]

Anvendelse af Z-Score

Z-scores bruges ofte til funktionsskalering for at bringe forskellige funktioner til en fælles skala. Normalisering af funktioner sikrer, at de har nul middelværdi og enhedsvarians, hvilket kan være gavnligt for visse maskinlæringsalgoritmer, især dem, der er afhængige af afstandsmål.
Z-scores kan bruges til at identificere outliers i et datasæt. Datapunkter med Z-score ud over en vis tærskel (normalt 3 standardafvigelser fra middelværdien) kan betragtes som outliers.
Z-scores kan bruges i anomalidetektionsalgoritmer til at identificere tilfælde, der afviger væsentligt fra den forventede adfærd.
Z-score kan anvendes til at transformere skæve fordelinger til mere normale fordelinger.
Når der arbejdes med regressionsmodeller, kan Z-scores af residualer analyseres for at kontrollere for homoskedasticitet (konstant varians af residualer).
Z-score kan bruges i funktionsskalering ved at se på deres standardafvigelser fra middelværdien.

Z-score vs. standardafvigelse

Z- Score	Standardafvigelse
Transform rådata til en standardiseret skala.	Måler mængden af variation eller spredning i et sæt værdier.
Gør det nemmere at sammenligne værdier fra forskellige datasæt, fordi de fjerner de originale måleenheder.	Standardafvigelse bevarer de oprindelige måleenheder, hvilket gør den mindre egnet til direkte sammenligninger mellem datasæt med forskellige enheder.
Angiv, hvor langt et datapunkt er fra gennemsnittet i form af standardafvigelser, hvilket giver et mål for datapunktets relative position inden for fordelingen	Udtrykt i de samme enheder som de originale data, hvilket giver et absolut mål for, hvor spredt værdierne er omkring middelværdien

Kontrollere: Z-score tabel

Hvorfor kaldes Z-scores Standard Scores?

Z-scores er også kendt som standardscores, fordi de standardiserer værdien af en tilfældig variabel. Det betyder, at listen over standardiserede score har et gennemsnit på 0 og en standardafvigelse på 1,0. Z-score giver også mulighed for sammenligning af score på forskellige slags variable. Dette skyldes, at de bruger relativ status til at sidestille scores fra forskellige variabler eller fordelinger.

genstart mysql ubuntu

Z-score bruges ofte til at sammenligne en variabel med en standard normalfordeling (med μ = 0 og σ = 1).