Et prisme er en tredimensionel solid figur med to identiske ender. Den består af flade sider, ens baser og lige tværsnit. Dens ansigter er parallellogrammer eller rektangler uden baser. Sådan et prisme, der har tre rektangulære flader og to parallelle trekantbaser, kaldes et trekantet prisme. De trekantede baser er forbundet med sideflader, der løber parallelt med hinanden.

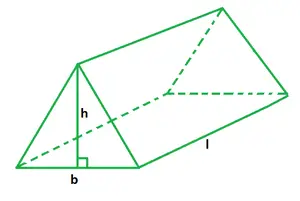
Volumen af ​​en trekantet prismeformel

Et trekantet prismes volumen er defineret som rummet inde i det eller rummet fyldt af det. At kende basisarealet og højden af ​​et trekantet prisme er alt, hvad der kræves for at beregne dets volumen. Rumfanget af et trekantet prisme er lig med produktet af basens areal og prismets højde, også kendt som prismets længde. Grundfladen af ​​et trekantet prisme er lig med halvdelen af ​​produktet af den trekantede base og dens højde.

Formel

V = (1/2) × b × h × l

hvor,

b er den trekantede base,

h er prismets højde,

l er længden af ​​prismet.

Prøveproblemer

Opgave 1. Find rumfanget af et trekantet prisme, hvis dets basis er 6 cm, højden er 8 cm og længden er 12 cm.

Løsning:

Vi har b = 6, h = 8 og l = 12.

html tags

Ved at bruge den formel vi har,

V = (1/2) × b × h × l

= (1/2) × 6 × 8 × 12

= 3 × 8 × 12

= 288 cu. cm

Opgave 2. Find rumfanget af et trekantet prisme, hvis dets basis er 5 cm, højden er 7 cm og længden er 8 cm.

Løsning:

udvidelsesfil java

Vi har b = 5, h = 7 og l = 8.

Ved at bruge den formel vi har,

V = (1/2) × b × h × l

= (1/2) × 5 × 7 × 8

= 5 × 7 × 4

= 140 cu. cm

Opgave 3. Find længden af ​​det trekantede prisme, hvis dets basis er 6 cm, højden er 9 cm og rumfanget er 98 cu. cm.

Løsning:

Vi har b = 6, h = 9 og V = 98.

Ved at bruge den formel vi har,

V = (1/2) × b × h × l

=> 98 = (1/2) × 6 × 9 × l

eksempler på binære træer

=> 196 = 27 l

=> l = 196/27

=> l = 7,25 cm

Opgave 4. Find højden af ​​det trekantede prisme, hvis dets basis er 8 cm, længden er 14 cm og volumen er 504 cu. cm.

Løsning:

Vi har, b = 8, l = 14 og V = 504.

Ved at bruge den formel vi har,

V = (1/2) × b × h × l

=> 504 = (1/2) × 8 × t × 14

=> 504 = 56 timer

=> h = 504/56

regressionsudtryk i java

=> h = 9 cm

Opgave 5. Find arealet af bunden af ​​det trekantede prisme, hvis dets længde er 18 cm, højden er 10 cm og volumen er 450 cu. cm.

Løsning:

Vi har, l = 18, h = 10 og V = 450.

Ved at bruge formlen for volumen vi har,

V = (1/2) × b × h × l

=> 450 = (1/2) × b × 10 × 18

=> 450 = 90b

=> b = 450/90

=> b = 5 cm

Derfor er arealet af trekantet base,

A = (1/2) × b × h

= (1/2) × 5 × 10

= 25 cm2