I matematik er der overalt en implementering af linje. Det er implementeret overalt, det vil sige i geometri, algebra og andre. Hældningen definerer linjens retning.
I denne artikel vil vi diskutere to typer skråninger, der er udefineret hældning og nul hældning. Før vi forstår typerne af hældning, lad os først se den korte beskrivelse af hældning.
Hvad er hældning?
Hældningen definerer stejlhed af linjen. Ordet 'stejlhed' betyder, hvor meget linjen er skrå. Med andre ord viser hældningen retningen af en linje på koordinatplanet. Således er det også kendt som gradienten af en linje. Rampe, trapper osv. er nogle af de virkelige eksempler på skråningen.
Sridevi
I matematik er hældningen forholdet mellem 'stigning' og 'løb' mellem to punkter. 'Rise' betyder den lodrette ændring i linjen, og 'Run' betyder den vandrette ændring i linjen.
Hældningen af en linje mellem to punkter (x1, og1) og (x2, og2) kan bestemmes ved at finde forskellen mellem punkternes koordinater. Hældningen af en linje er generelt repræsenteret med bogstavet 'm'.
m = Δx/Δy = (y2- og1)/(x2- x1)eller, m = stige/løbe
Udefineret hældning
Den udefinerede hældning er hældningen af den lodrette linje. Det betyder, at hvis linjen er lodret, er hældningen udefineret. Linjen i den udefinerede hældning er parallel med y-aksen, og værdien af ?x er 0. X-koordinaten for udefineret hældning ændres aldrig, uanset hvad y-koordinaten er. I en udefineret hældning er værdien af Δy et ikke-nul heltal, hvorimod værdien af Δx er 0. Den udefinerede hældning er modsat nulhældningen. Med hensyn til stigning og løb er stigningen i udefineret hældning enten positiv eller negativ, og kørsel i den udefinerede hældning er nul.
m = Δy/Δx = positiv eller negativ Δy/0Den udefinerede værdi af m repræsenterer den udefinerede hældning og den lodrette linje.
I den følgende graf kan du se repræsentationen af en udefineret hældning. Linjen i nedenstående graf er parallel med y-aksen, der angiver den udefinerede hældning.
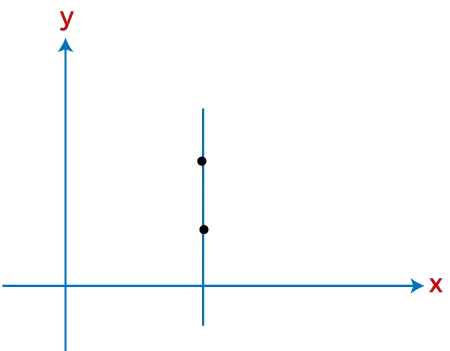
Fig: Repræsentation af udefineret hældning
I ovenstående billede er der en lodret linje, som angiver den udefinerede hældning.
Nul hældning
I nulhældningen er linjen parallel med x-aksen, og y-koordinaten ændres aldrig. Det er hældningen af den vandrette linje. Med hensyn til stigning og løb er stigningen i nulhældningen 0, og stigningen i nulhældningen er positiv.
m = Δy/Δx = 0/positiv ΔxHvis værdien af m er lig med nul, er linjen vandret og har en konstant hældning.
I den følgende graf kan du se repræsentationen af nulhældning. Linjen i nedenstående graf er parallel med x-aksen, der angiver nulhældningen, og y i nulhældningen forbliver den samme, uanset hvad x er.

Fig: Repræsentation af nulhældning
I ovenstående billede er der en vandret linje, som angiver nulhældningen.
Lad os nu se forskellen mellem en udefineret hældning og en nulhældning.
Forskellen mellem udefineret hældning og nul hældning
Den udefinerede hældning er modsat nulhældningen. Forskellen mellem den udefinerede hældning og nulhældningen er opstillet som følger -
| Ja Nej. | Udefineret hældning | Nul hældning |
|---|---|---|
| 1. | Det bestemmes af variablen X. | Det bestemmes af variablen Y. |
| 2. | Det er hældningen af den lodrette linje. | Det er hældningen af den vandrette linje. |
| 3. | Den udefinerede hældning har ikke nogen konkret værdi, så den har en ikke-eksisterende værdi. | Nulhældning er en bestemt værdi, dvs. nul. |
| 4. | Nævneren af den udefinerede hældning er nul. | Tælleren for nulhældningen er nul. |
| 5. | I en udefineret hældning ændres Y, men X ændres ikke. | I en udefineret hældning ændres X, men Y ændres ikke. |
Det handler om artiklen. Vi har forsøgt at give dig tilstrækkelig information på en nemmere måde. Håber det er gavnligt for dig og giver dig information om udefineret hældning, nul hældning og deres sammenligning.
