Det Tidskompleksitet af Merge Sort er O(n log n) i både gennemsnit og værste tilfælde . Rumkompleksiteten af Flet sortering er På) . 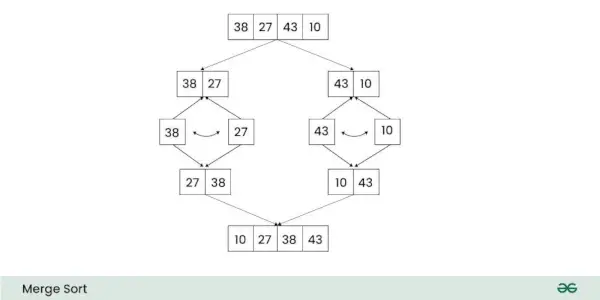
forekomst af
| Aspekt | Kompleksitet |
|---|---|
| Tidskompleksitet | O(n log n) |
| Rumkompleksitet | På) |
Tidskompleksitetsanalyse af fletningssortering:
Overvej følgende terminologier:
T(k) = tid det tager at sortere k elementer
M(k) = tid det tager at flette k elementer
Så det kan skrives
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + konstant * N
Disse N/2-elementer er yderligere opdelt i to halvdele. Så,
streng format java
T(N) = 2 * [2 * T(N/4) + konstant * N/2] + konstant * N
= 4 * T(N/4) + 2 * N * konstant
. . .
= 2k* T(N/2k) + k * N * konstant
Den kan maksimalt deles, indtil der er et element tilbage. Så, så N/2k= 1. k = log 2 N
T(N) = N * T(1) + N * log2N * konstant
= N + N * log2Nboolsk i c
Derfor er tidskompleksiteten O(N * log 2 N) .
Så i det bedste tilfælde, det værste tilfælde og det gennemsnitlige tilfælde er tidskompleksiteten den samme.
Rumkompleksitetsanalyse af fletningssortering:
Flet sortering har en rummets kompleksitet af På) . Dette skyldes, at den bruger et hjælpearray af størrelse n for at flette de sorterede halvdele af input-arrayet. Hjælpe-arrayet bruges til at gemme det flettede resultat, og input-arrayet overskrives med det sorterede resultat.
