Tre dimensioner kan måles, længde, bredde og højde, for ethvert objekt, du kan se eller røre ved. Der er visse dimensioner af vores hjem, som vi bor i. Den rektangulære skærm/monitor, du ser på, har en bredde og bredde i længden. For hver tredimensionel geometrisk struktur måles overfladeareal og volumen.
Aera dækket af objektets overflade er overfladearealet af et givet objekt. Hvorimod mængden af ledig plads i et objekt er volumen.
Indholdsfortegnelse
- Overfladeareal
- Samlet overfladeareal
- Buet overfladeareal/lateral overfladeareal
- Bind
- Eksempler på overfladearealer og volumener
- Ofte stillede spørgsmål om formler for overfladeareal og volumen
Overfladeareal
Overfladeareal og volumen kan beregnes for enhver tredimensionel (3D)geometrisk form. Overfladen af ethvert område er det område, der er optaget af overfladen af et objekt. Volumen er mængden af ledig plads i et objekt. Vi har forskellige former for former som en halvkugle, kugle, terning, terning, cylinder osv. Alle tredimensionelle former har areal og volumen. Men to-dimensionelle former som firkanter, rektangler, trekanter, cirkler osv.
Her i to-dimensional kan vi kun måle arealet. Det areal, der optages af et tredimensionelt objekt af dets ydre overflade, kaldes overfladearealet. Det måles i kvadratenheder.
Området er af to typer:
- Samlet overfladeareal
- Buet overfladeareal/lateral overfladeareal
Samlet overfladeareal
Arealet inklusive basen(e) og den buede del svarer til det samlede overfladeareal. Det er mængden af det område, der er omsluttet af objektets overflade. Hvis formen har en buet base og overflade, vil summen af de to områder være det samlede areal. Det samlede overfladeareal kan defineres som det samlede areal, der dækkes af en genstand, inklusive dens base såvel som den buede del. Hvis en genstand har både grundfladen og buet areal, vil det samlede overfladeareal være lig med summen af basis og buet område.
- Det samlede overfladeareal er det samlede areal optaget af et objekt.
- Tag f.eks. en kuboid som et eksempel, cuboiden har 6 flader, 12 kanter og 8 spidser.
Samlet overfladeareal = basisareal + buet område
pyspark sql
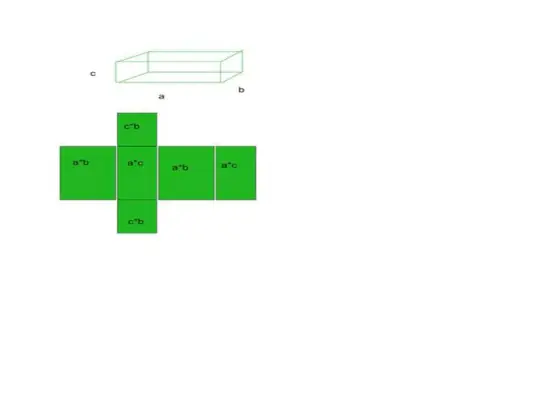
- Summen af alle disse i alt 6 områder vil være vores samlede overfladeareal af den bestemte form
Eksempel:
Nedenstående er en kuboid, hvis dimension er angivet som længde = 8 cm, bredde = 4 cm og højde = 6 cm, find TSA for en cuboid
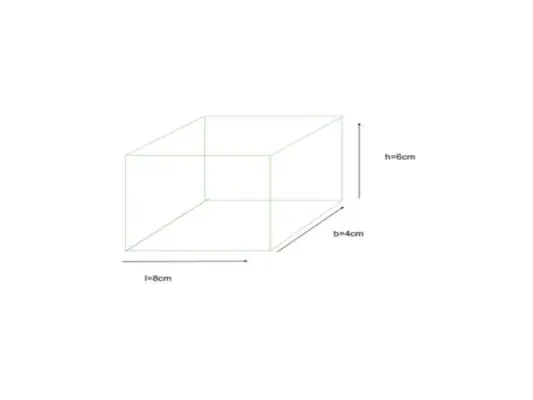
givet l = 8 cm, b = 4 cm, h = 6 cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
TSA for kuben er 208 cm.
Buet overfladeareal/lateral overfladeareal
Buet overfladeareal, undtagen dets centrum, svarer til arealet af kun den buede del af formen/formerne. For former som en kegle kaldes det ofte det laterale overfladeareal. Det laterale overfladeareal kan defineres som det område, der kun inkluderer det buede overfladeareal af et objekt eller et lateralt overfladeareal af et objekt ved at ekskludere basisarealet af et objekt. Det laterale overfladeareal er også kendt som det buede overfladeareal.
De fleste af formerne eller objekterne refererer til det buede overfladeareal, formen eller den objektlignende cylinder refererer til det som et lateralt overfladeareal. Enkelt sagt kaldes det område, der er synligt for os, et lateralt overfladeareal. Betragt for eksempel cylinderen som vist i nedenstående figur.
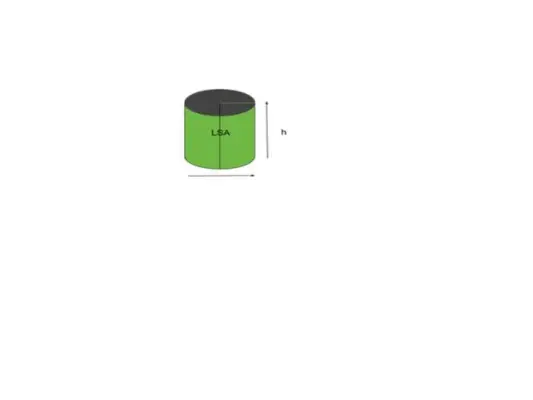
Bind
Volumen er mængden af plads i et bestemt 3D-objekt. Den samlede mængde plads, som et objekt eller stof optager kaldes volumen. Det måles i kubikenheder.
Formler for overfladeareal og volumen
Den angivne tabel indeholder det samlede overfladeareal, det buede overfladeareal/laterale overfladeareal og volumen af forskellige former.
| Formens navn | Buet overfladeareal | Samlet overfladeareal | Bind |
|---|---|---|---|
| Cuboid | 2 timer (l + b) | 2(lb + bh + hl) | l * b * h |
| terning | 4a2 | 6a2 | -en3 |
| Cylinder | 2πrh | 2π(r + h) | πr2h |
| Kugle | 4πr2 indsættelsessorteringsalgoritme | 4πr2 | 4/3π r3 |
| Kegle | πrl | πr(r + l) | 1/3π r2h |
| Halvkugle | 2pr2 | 3πr2 | 2/3π r3 |
Læs mere:
- Pyramidens overfladeareal
- Cylinderens overfladeareal
- Overfladeareal af halvkugle
- Sfærens overfladeareal
- Overfladeareal af Cuboid
Eksempler på overfladearealer og volumener
Eksempel 1: 2 terninger hver med volumen 512 cm 3 er sammenføjet ende mod ende. Find overfladearealet af den resulterende kasse?
Løsning:
givet,
Volumen (V) af hver terning er = 512 cm3
vi kan nu antyde, at en3= 512 cm3
∴ Side af terningen, dvs. a = 8 cm
Nu vil bredden og længden af den resulterende cuboid være 8 cm hver, mens dens højde vil være 16 cm.
Så overfladearealet af kuboidet (TSA) = 2(lb + bh + lh)
Nu, ved at sætte værdierne, får vi,
= 2(8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Derfor er kuboidens TSA = 640 cm 2
Eksempel 2: Vi har et cylindrisk lys, 14 cm i diameter og længde 2 cm. Det smeltes til et kubisk lys med dimensionerne 7 cm × 11 cm × 1 cm. Hvor mange kubiske stearinlys kan man få?
Løsning:
Dimensioner på det cylindriske stearinlys:
Radius af cylindrisk stearinlys = 14/2 cm = 7 cm
Højde/tykkelse=2 cm
Volumen af et cylindrisk lys = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Rumfang af kuboid stearinlys = 7 x 11 x 1 = 77 cm3
Derfor er antallet af kubiske stearinlys = Volumen af kubisk stearinlys/volumen af et cylindrisk stearinlys = 308/77 = 4
Derfor kan vi få 4 kubiske stearinlys.
Eksempel 3: En kvinde vil bygge en kugleformet legetøjskugle af ler, hvis radius er lig med radius af armringen, hun har på. Da armringen er cirkulær i form, ønsker hun også, at armringens areal er lig med kuglens rumfang. Find ud af radius af armringen, hun har på?
Løsning:
Lad r være armringens radius såvel som kuglen,
Vi har fået, at kuglens rumfang er lig med armringens areal:
Derfor,
πr2= 4/3 πr3
⇒ r = 3/4
Derfor er armringens radius 3/4 enheder.
Eksempel 4: Det er givet, at skråhøjden af en ret cirkulær kegle er 25 cm og dens højde er 24 cm. Find det buede overfladeareal af keglen?
Løsning:
Formlen for keglens buede overfladeareal er πrl. Hvor r er keglens radius og l er keglens skråhøjde.
Her er keglen den højre cirkulære kegle.
Så radius af keglen ville være:
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
sortere en arraylist=> r = 7 cm.
Beregning af den buede overflade er nu:
Nødvendigt område = (22/7) * 7 * 25 = 550 cm2
Derfor er det buede overfladeareal af keglen 550 cm 2 .
Eksempel 5: Find det laterale overfladeareal af en cylinder med en basisradius på 6 tommer og en højde på 14 tommer.
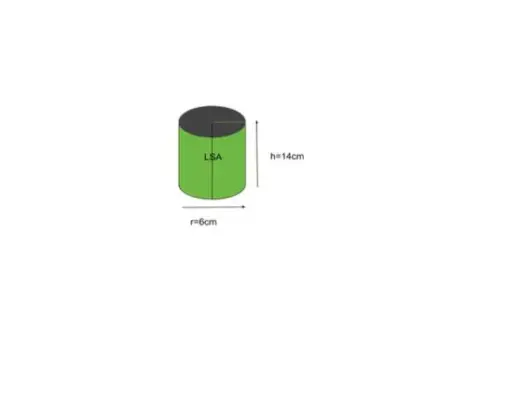
Løsning:
Givet radius r = 6, højde h = 14
LSA = 2µrh
= 2 * ¸ * 6 * 14
= 168µ
= 527.787
= 528.
LSA for den givne cylinder er 528 cm .
Praksisspørgsmål om overfladearealer og volumener
Forskellige Praksisspørgsmål om overfladearealer og volumen formlerne er:
Q1. Find overfladearealet af en terning med sidelængde 5 centimeter.
Q2. Beregn rumfanget af en kugle med en radius på 3 meter.
Q3. Bestem det samlede overfladeareal af en cylinder med radius 4 centimeter og højde 8 centimeter.
Q4. Find volumen af en kegle med radius 6 tommer og højde 10 tommer.
Q5. Beregn overfladearealet af et rektangulært prisme med længde 7 meter, bredde 4 meter og højde 6 meter.
Ofte stillede spørgsmål om formler for overfladeareal og volumen
Hvad er formlerne for overfladeareal og volumen?
Forskellige formler for overfladeareal og volumen er tilføjet i artiklen ovenfor.
Hvad er formlen for overfladearealvolumen Klasse 10?
Formel for overfladeareal og volumenklasse 10 indeholder:
| Formens navn | Buet overfladeareal | Samlet overfladeareal | Bind |
|---|---|---|---|
| Cuboid ændre tilføje kolonne orakel | 2 timer (l + b) | 2(lb + bh + hl) | l × b × h |
| terning | 4a2 | 6a2 | -en3 |
| Cylinder | 2πrh | 2π(r + h) | πr2h |
| Kugle | 4πr2 | 4πr2 | 4/3π r3 |
| Kegle | πrl | πr(r + l) | 1/3π r2h |
| Halvkugle | 2pr2 | 3πr2 | 2/3π r3 |
Hvad er formlen for Cuboid i overfladeareal og volumen?
- Overfladeareal af Cuboid = 2(lb + bh + hl)
- Rumfang af Cubiod = l × b × h
Hvad er overfladeareal og volumen?
Overfladeareal er arealet af alle overflader af et fast stof, og dets volumen er det rum, som sløjden optager.
