Standardformen for en parabel er y = akse2+ bx + c hvor a, b og c er reelle tal, og a ikke er lig med nul. En parabel er defineret som mængden af alle punkter i et plan, der er lige langt fra en fast linje og et fast punkt i planet.
I denne artikel vil vi forstå, hvad en parabel er, standardligningen for en parabel, relaterede eksempler og andre i detaljer.
Indholdsfortegnelse
Hvad er en parabel?
En parabel er et keglesnit defineret som mængden af alle punkter, der er lige langt fra et punkt kaldet fokus og en linje kaldet direkte. Standardligningerne for en parabel afhænger af dens orientering (åbningsretning) og position.
Ligning af en parabel
Parabelligning kan skrives i standardform eller generel form, og begge er tilføjet nedenfor:
Generelle ligninger af en parabel
Den generelle ligning for en parabel er,
y = 4a(x – h) 2 + k
(eller)
x = 4a(y – k) 2 + h
Hvor (h, k) er toppen af en parabel.
Standardligninger for en parabel
Standardligningen for en parabel er,
y = akse 2 + bx + c
(eller)
x = er 2 + af + c
hvor a aldrig kan være nul.
Dele af en parabel
Nogle vigtige udtryk og dele af en parabel er:
- Fokus: Fokus er det faste punkt i en parabel.
- Direkte: En parabels retning er linjen vinkelret på en parabels akse.
- Fokalakkord: Den akkord, der passerer gennem fokus på en parabel, skærer parablen på to forskellige punkter, kaldes den fokale akkord.
- Brændvidde: Brændvidden er afstanden til et punkt (x1, og1) på parablen fra fokus.
- Højre side: En latus rectum er en fokal akkord, der passerer gennem fokus på en parabel og er vinkelret på parablens akse. Længden af latus rectum er LL' = 4a.
- Excentricitet: Forholdet mellem afstanden af et punkt fra fokus og dets afstand fra dirrix kaldes excentricitet (e). For en parabel er excentricitet lig med 1, dvs. e = 1.
En parabel har fire standardligninger baseret på orienteringen af parablen og dens akse. Hver parabel har en anden tværgående akse og konjugeret akse.
| Parabels ligning | Parabel | Formler for parametre for en parabel |
|---|---|---|
| og 2 = 4 aks | 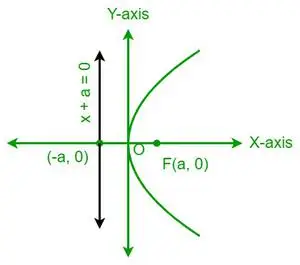 Vandret parabel |
|
| og 2 = -4aks |  Vandret parabel |
|
| x 2 = 4 ay |  Lodret parabel |
|
| x 2 = -4ay |  Lodret parabel |
|
Følgende er observationerne lavet fra standardformen af ligninger for en parabel:
- En parabel er symmetrisk med dens akse. For eksempel, y2= 4ax er symmetrisk v.r.t. x-aksen, hvorimod x2= 4ay er symmetrisk i forhold til y-aksen.
- Hvis en parabel er symmetrisk om x-aksen, åbner parablen sig mod højre, hvis x-koefficienten er positiv, og mod venstre, hvis x-koefficienten er negativ.
- Hvis en parabel er symmetrisk om y-aksen, åbner parablen sig opad, hvis y-koefficienten er positiv, og nedad, hvis y-koefficienten er negativ.
Følgende er standardligningerne for en parabel, når symmetriaksen enten er parallel med x-aksen eller y-aksen, og toppunktet ikke er ved origo.
| Parabolens ligning | Parabel | Formler for parametre for en parabel |
|---|---|---|
| (og – k)2= 4a(x – h) |  Vandret parabel |
|
| (og – k)2= -4a(x – h) |  Vandret parabel |
|
| (x – h)2= 4a(y – k) |  Lodret parabel |
|
| (x – h)2= -4a(y – k) |  Lodret parabel |
|
Ligning af parabelafledning
Lad P være et punkt på parablen, hvis koordinater er (x, y). Fra definitionen af en parabel er afstanden fra punktet P til fokus (F) lig med afstanden af det samme punkt P til en parabels retning. Lad os nu betragte et punkt X på linjen, hvis koordinater er (-a, y).
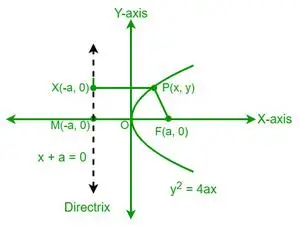
Fra definitionen af en parabels excentricitet har vi
e = PF/PX = 1
⇒ PF = PX
Koordinaterne for fokus er (a, 0). Nu kan vi ved at bruge koordinatafstandsformlen finde afstanden fra punktet P (x, y) til fokus F (a, 0).
PF = √[(x – a)2+ (og – 0)2]
⇒ PF = √[(x – a)2+ og2] ------ (1)
Ligningen for directrix er x + a = 0. For at finde afstanden til PX bruger vi den vinkelrette afstandsformel.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
Vi ved allerede, at PF = PX. Så lig ligning (1) og (2).
√[(x – a)2+ og2] = (x + a)
Ved at kvadrere på begge sider får vi,
⇒ [(x – a)2+ og2] = (x + a)2
⇒ x2+ a2– 2ax + y2= x2+ a2+ 2 aks
⇒ og2– 2ax = 2ax
⇒ og2= 2ax + 2ax ⇒ og 2 = 4 aks
Således har vi udledt ligningen for en parabel. På samme måde kan vi udlede standardligningerne for de tre andre parabler.
- og2= -4aks
- x2= 4 ay
- x2= -4ay
og 2 = 4ax, og 2 = -4aks, x 2 = 4ay og x 2 = -4 år er standardligningerne for en parabel.
Artikler relateret til parabel:
- Cirkelligning
- Ellipseligning
- Ligning af hyperbel
- Anvendelser af parabel i det virkelige liv
Eksempler på ligning af en parabel
Eksempel 1: Find længden af latus rectum, fokus og toppunkt, hvis ligningen for parablen er y 2 = 12x.
Løsning:
givet,
Parablens ligning er y2= 12x
Ved at sammenligne den givne ligning med standardformen y2= 4 aks
4a = 12
⇒ a = 12/4 = 3
Vi ved det,
Højre side af en parabel = 4a = 4 (3) = 12
Nu, fokus for parablen = (a, 0) = (3, 0)
Toppunktet for den givne parabel = (0, 0)
Eksempel 2: Find ligningen for parablen, som er symmetrisk om X-aksen, og går gennem punktet (-4, 5).
Løsning:
givet,
Parabel er symmetrisk om X-aksen og har sit toppunkt i origo.
Således kan ligningen have formen y2= 4ax eller y2= -4ax, hvor tegnet afhænger af om parablen åbner sig mod venstre eller højre side.
Parabel skal åbne til venstre, da den passerer gennem (-4, 5), som ligger i anden kvadrant.
Så ligningen vil være: y2= -4aks
Substituere (-4, 5) i ovenstående ligning,
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Derfor er ligningen for parablen: y2= -4(25/16)x (eller) 4y2= -25x.
Eksempel 3: Find koordinaterne for fokus, aksen, ligningen for retningslinjen og latus rectum af parablen x 2 = 16 år.
Løsning:
givet,
Parablens ligning er: x2= 16 år
Ved at sammenligne den givne ligning med standardformen x2= 4ay,
4a = 16 ⇒ a = 4
Koefficienten for y er positiv, så parablen åbner sig opad.
Desuden er symmetriaksen langs den positive Y-akse.
Derfor,
Fokus for parablen er (a, 0) = (4, 0).
Ligningen for rettet er y = -a, dvs. y = -4 eller y + 4 = 0.
Længde af latus rectum = 4a = 4(4) = 16.
Eksempel 4: Find længden af latus rectum, fokus og toppunkt, hvis ligningen for en parabel er 2(x-2) 2 + 16 = y.
Løsning:
givet,
Ligningen for en parabel er 2(x-2)2+ 16 = og
Ved at sammenligne den givne ligning med den generelle ligning for en parabel y = a(x – h)2+ k, vi får
a = 2
(h, k) = (2, 16)
Vi ved det,
Længde af latus rectum af en parabel = 4a
= 4(2) = 8
Nu, fokus= (a, 0) = (2, 0)
Nu, Vertex = (2, 16)
Eksempel 5: Ligningen for en parabel er x 2 – 12x + 4y – 24 = 0, og find derefter dets toppunkt, fokus og retning.
Løsning:
givet,
Parablens ligning er x2– 12x + 4y – 24 = 0
⇒ x2– 12x + 36 – 36 + 4y – 24 = 0
⇒ (x – 6)2+ 4 år – 60 = 0
⇒ (x – 6)2= -4(y + 15)
Den opnåede ligning er i form af (x – h)2= -4a(y – k)
-4a = -4 ⇒ a = 1
Så toppunktet = (h, k) = (6, – 15)
Fokus = (h, k – a) = (6, -15-1) = (6, -16)
Ligningen for retningslinjen er y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
Ofte stillede spørgsmål om ligning af parabel
Hvordan finder man standardligningen for en parabel?
Standardform for parabel er y2= 4ax eller x2= 4 ay.
Hvad er den normale ligning for parabel?
Normalligning til parablen y2= 4akse med en hældning m er givet som: y = mx – 2 am – am 3
Hvordan finder du toppunktet på en parabel?
For givet parabel: y = akse2+ bx + c dens toppunkt kan findes ved hjælp af formlen x = − b/2a. Sæt denne x-værdi tilbage i ligningen for at finde den tilsvarende y-koordinat.
pyspark tutorial
