Sin Cos formler i trigonometri: Trigonometri er, som navnet antyder, studiet af trekanter. Det er en vigtig gren af matematikken, der studerer forholdet mellem sidelængder og vinkler i den retvinklede trekant og hjælper også med at bestemme de manglende sidelængder eller vinkler i en trekant. Der er seks trigonometriske forhold eller funktioner: sinus, cosinus, tangens, cosekant, sekant og cotangens, hvor cosekant, sekant og cotangens er de gensidige funktioner af de andre tre funktioner, dvs. henholdsvis sinus, cosinus og tangent.
Et trigonometrisk forhold defineres som forholdet mellem sidelængderne af en retvinklet trekant. Trigonometri bruges på forskellige områder i vores daglige liv. Det hjælper med at bestemme højderne af bakker eller bygninger. Det bruges også inden for områder som kriminologi, konstruktion, fysik, arkæologi, marinemotorteknik osv.
I denne artikel vil vi udforske alt trigonometri formler for det meste sin og cos formler med deres eksempler, og en liste over alle formler i trigonometri.
Indholdsfortegnelse
- Formler i trigonometri
- Nogle grundlæggende Sin Cos-formler
- Sin Cos formler tabel
- Eksempler på Sin Cos-formler
- Øv problemer på Sin Cos-formler i trigonometri med eksempler
Formler i trigonometri
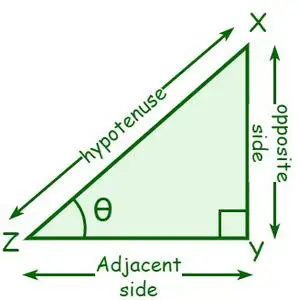
Lad os betragte en retvinklet trekant XYZ, hvor ∠Y = 90°. Lad vinklen ved toppunktet Z være θ. Siden, der støder op til θ, kaldes den tilstødende side, og siden modsat θ kaldes den modsatte side. En hypotenuse er en side modsat den rette vinkel eller den længste side af en ret vinkel.
- sin θ = Modsat side/hypotenuse
- cos θ = Tilstødende side/Hypotenuse
- tan θ = Modsat side/tilstødende side
- cosec θ = 1/sin θ = Hypotenuse/Modsat side
- sek θ = 1/ cos θ = Hypotenuse/tilstødende side
- barneseng θ = 1/ tan θ = Tilstødende side/Modsatte side
Sinus Formel
Sinus for en vinkel i en retvinklet trekant er forholdet mellem længden af den modsatte side og længden af hypotenusen til den givne vinkel. En sinusfunktion er repræsenteret som sin.
sin θ = Modsat side/hypotenuse
Cosinus formel
Cosinus af en vinkel i en retvinklet trekant er forholdet mellem længden af den tilstødende side og længden af hypotenusen til den givne vinkel. En cosinusfunktion er repræsenteret som cos.
python __navn__cos θ = Tilstødende side/Hypotenuse
Nogle grundlæggende Sin Cos-formler
Sinus- og cosinusfunktioner i kvadranter
- Sinusfunktionen er positiv i første og anden kvadrant og negativ i tredje og fjerde kvadrant.
- Cosinusfunktionen er positiv i første og fjerde kvadrant og negativ i anden og tredje kvadrant.
grader
Kvadrant
Tegn på sinusfunktion
Tegn på Cosinus funktion
0° til 90°
1. kvadrant
+ (positiv)
+ (positiv)
90° til 180°
2. kvadrant
+ (positiv)
– (negativ)
180° til 270°
3. kvadrant
– (negativ)
– (negativ)
270° til 360°
4. kvadrant
– (negativ)
+ (positiv)
Sinus- og cosinusfunktionernes negative vinkelidentitet
- Sinus for en negativ vinkel er altid lig med vinklens negative sinus.
sin (– θ) = – sin θ
- Cosinus for en negativ vinkel er altid lig med vinklens cosinus.
cos (– θ) = cos θ
Forholdet mellem sinus- og cosinusfunktion
sin θ = cos (90° – θ)
Gensidige funktioner af sinus- og cosinusfunktionerne
- En Cosecant-funktion er sinusfunktionens gensidige funktion.
cosec θ = 1/sin θ
- En sekantfunktion er den gensidige funktion af cosinusfunktionen.
sek θ = 1/cos θ
Pythagoras identitet
uden 2 θ + cos 2 θ = 1
Periodiske identiteter af sinus- og cosinusfunktionerne
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Dobbeltvinkelformler for sinus- og cosinusfunktionerne
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – synd 2 θ = 2 cos 2 θ – 1 = 1 – 2 sin 2 jeg
Halvvinkelidentiteter for sinus- og cosinusfunktionerne
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Triple vinkelidentiteter for sinus- og cosinusfunktionerne
sin 3θ = 3 sin θ – 4 sin 3 jeg
cos 3θ = 4cos 3 θ – 3 cos θ
Sum- og differensformler
- Sinus funktion
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- Cosinus funktion
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Sinusloven eller sinusreglen
Sinusloven for sinusreglen er en trigonometrisk lov, der giver en sammenhæng mellem sidelængderne og vinklerne i en trekant.

a/sin A = b/sin B = c/sin C
Hvor a, b og c er længderne af de tre sider af trekanten ABC, og A, B og C er vinklerne.
Cosinusloven
Cosinusloven for cosinusreglen bruges til at bestemme de manglende eller ukendte vinkler eller sidelængder af en trekant.

-en 2 = b 2 + c 2 – 2bc cos A
b 2 = c 2 + a 2 – 2ca cos B
c 2 = a 2 + b 2 – 2ab cos C
Hvor a, b og c er længderne af de tre sider af trekanten ABC, og A, B og C er vinklerne.
Sin Cos formler tabel
Her er Sin- og Cos-formeltabellen/-listen for forskellige vinkler i grader og i radianer:
Sin Cos formler liste
| Vinkel (i grader) | Vinkel (i radianer) | synd i | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | s/6 | 1/2 | _3/2 |
| 45° | s/4 | 1/√2 | 1/√2 |
| 60° | s/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Eksempler på Sin Cos-formler
Opgave 1: Hvis cos α = 24/25, så find værdien af sin α.
Løsning:
givet,
cos a = 24/25
Fra de pythagoræiske identiteter har vi;
int til strengcos2θ + sin2θ = 1
(24/25)2+ uden2α = 1
uden2α = 1 – (24/25)2
uden2α = 1 – (576/625) = (625 – 576)/625
uden2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Derfor er sin α = ±7/25.
Opgave 2: Bevis formlerne for sin 2A og cos 2A, hvis ∠A= 30°.
Løsning:
Givet, ∠A= 30°
Vi ved det,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Siden, sin 30° = 1/2, cos 30° = √3/2 og sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Siden, cos 60° = 1/2 og cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Derfor bevist.
Opgave 3: Find værdien af cos x, hvis tan x = 3/4.
Løsning:
Givet, tan x = 3/4
Vi ved det,
tan x = modsat side/tilstødende side = 3/4
For at finde hypotenusen bruger vi Pythagoras sætning:
hypotenusen2= modsat2+ tilstødende2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Nu, cos x = tilstødende side/hypotenuse
cos x = 4/5
Værdien af cos x er således 4/5.
Opgave 4: Find ∠C (i grader) og ∠A (i grader), hvis ∠B = 45°, BC = 15 tommer og AC = 12 tommer.

Løsning:
Givet: ∠B = 45°, BC = a = 15 tommer og AC = b = 12 tommer.
Fra sinusloven har vi
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ uden A = 15/16,97 = 0,8839
⇒ ∠A = synd-1(0,8839) = 62,11°
Vi ved, at summen af indvendige vinkler i en trekant er 180°.
Så ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Derfor er ∠A = 62,11° og ∠C = 72,89°.
Opgave 5: Bevis halvvinkelidentiteter for cosinusfunktionen.
Løsning:
Cosinusfunktionens halvvinkelidentitet er:
cos (θ/2) = ±√[(1 + cos θ)/2]
Fra dobbeltvinkelidentiteter har vi,
cos 2A = 2 cos2A – 1
Udskift nu A med θ/2 på begge sider
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Derfor bevist.
Øv problemer på Sin Cos-formler i trigonometri med eksempler
1. Givet sin θ = 3/5. Find cos θ.
2. Bevis identiteten sin(2A) = 2 sinA cosA for A=45∘.
3. Hvis cos α = 5/13. Find synd(2a).
4. Løs for θ hvis sin θ = cos(90∘−θ).
5. Hvis tan β = 2. Find sin β og cos β ved hjælp af den pythagoræiske identitet.
Ofte stillede spørgsmål om Sin Cos-formler i trigonometri med eksempler
Hvad er de grundlæggende sinus- og cosinusformler i trigonometri?
De grundlæggende sinus- og cosinusformler er sin θ = Modsat/Hypotenuse og cos θ = Adjacent/Hypotenuse, hvor θ er en vinkel i en retvinklet trekant.
Hvordan finder man sinus og cosinus for specielle vinkler?
Specielle vinkler som 0∘, 30∘, 45∘, 60∘ og 90∘ har specifikke sinus- og cosinusværdier, der kan huskes ved hjælp af trigonometriske tabeller eller enhedscirkelkoncepter.
Hvad er forholdet mellem sinus- og cosinusfunktioner?
Sinus- og cosinusfunktionerne er forbundet med identiteten sin θ = cos(90∘- θ) og den pythagoræiske identitet uden 2 θ+cos 2 θ = 1.
Hvordan bruger man dobbeltvinkelformlerne for sinus og cosinus?
Dobbeltvinkelformlerne er sin(2θ) = 2sinθcosθ og cos(2θ)=cos 2 θ – synd 2 jeg. Disse bruges til at udtrykke trigonometriske funktioner af dobbeltvinkler i form af enkeltvinkler.
Hvordan finder man værdierne af sinus og cosinus for vinkler i forskellige kvadranter?
Tegnene for sinus- og cosinusfunktioner afhænger af kvadranten, hvori vinklen ligger:
- Første kvadrant: sin θ> 0 og cos θ> 0
- Anden kvadrant: sin θ> 0 og cos θ <0
- Tredje kvadrant: sinθ <0 og cosθ < 0
- Fjerde kvadrant: sinθ 0
