Kvadrant er defineret som et område i rummet, der er opdelt i fire lige store dele af to akser, nemlig X-aksen og Y-aksen i det kartesiske plan. Disse to akser skærer hinanden i 90 grader, og de fire således dannede områder kaldes fire kvadranter, nemlig I-kvadrant, II-kvadrant, III-kvadrant og IV-kvadrant.
heltal dobbelt java
I denne artikel vil vi udforske væsentlige kvadrantbegreber, herunder hvad en kvadrant er, dens areal, kvadrantgraf, kartesisk plan, fortegnskonventioner inden for kvadranten, abscisse og koordinat, samt plotning af punkter på en kvadrant.
Indholdsfortegnelse
- Hvad er Quadrants of Graph?
- Underskriv konvention i kvadranter
- Plotte punkter på kvadranter
- Trigonometriske værdier i forskellige kvadranter
Hvad er Quadrants of Graph?
En kvadrant er et udpeget område på en Kartesisk fly , skabt af krydset mellem X- og Y-akserne. I dette plan dannes fire kvadranter, hver med sine unikke træk. Den første kvadrant, øverst til højre, har positive x- og y-koordinater. Den anden kvadrant, øverst til venstre, har negative x- og positive y-koordinater og så videre. At forstå disse kvadranter er afgørende for at lokalisere og fortolke punkter på grafen, hvilket giver en systematisk måde at navigere og analysere kartesiske koordinater på.
4 kvadranter på koordinatplan
Det kartesiske plan, dannet af X- og Y-akserne, er opdelt i fire kvadranter, hver med særskilte karakteristika:
- Første kvadrant: Placeret øverst til højre er både x- og y-koordinater positive. Denne kvadrant repræsenterer punkter i den øverste højre del af planet.
- Anden kvadrant: Placeret øverst til venstre er x-koordinaten negativ, og y-koordinaten er positiv. Denne kvadrant dækker punkter i den øverste venstre del af planet.
- Tredje kvadrant: Placeret nederst til venstre er både x- og y-koordinater negative. Punkter i det nederste venstre område af flyet falder ind i denne kvadrant.
- Fjerde kvadrant: Findes nederst til højre er x-koordinaten positiv, og y-koordinaten er negativ. Denne kvadrant inkluderer punkter i den nederste højre del af planet.
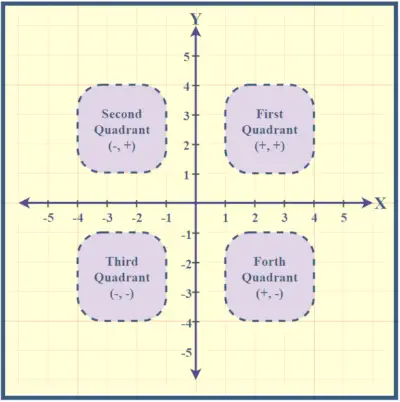
Kvadranterne er nummereret i retning mod uret, startende fra øverst til højre. Punktet, hvor X- og Y-akserne skærer hinanden, kaldes origo, med koordinater (0,0), der angiver nulværdier for både x og y. At forstå disse kvadranter hjælper med at lokalisere punkter inden for det kartesiske plan.
Hvad er oprindelse?
Udgangspunktet på en graf, kendt som origo og vist som (0, 0), er hvor den vandrette x-akse og den lodrette y-akse skærer hinanden. Det betyder, at ved origo er værdierne for både x og y nul. Det tjener som referencepunkt til at lokalisere andre punkter på grafen. På billedet tilføjet ovenfor viser punkt O oprindelsen.
Abscisse og Ordinat i Kvadranter
I de fire kvadranter er tal repræsenteret som par (a, b), hvor 'a' står for x-koordinaten og 'b' for y-koordinaten. For at finde ud af, hvor et punkt er uden at plotte, skal du være opmærksom på fortegnene for x-koordinat (abscisse) og y-koordinat (ordinat). For eksempel, hvis du har et punkt som Q (3, -5), indikerer tegnene (+ve, -ve) at det er i kvadrant IV.
Abscissen viser den vandrette afstand fra Y-aksen. En positiv abscisse betyder til højre, og i vores eksempel betyder abscisse = 3 går lige fra origo langs x-aksen med 3 enheder.
Ordinaten angiver den lodrette afstand fra oprindelsen. En negativ ordinat betyder at gå ned fra origo langs y-aksen. I eksemplet betyder ordinat = -5 gå ned med 5 enheder.
Underskriv konvention i kvadranter
Tegnkonventioner i kvadranterne kan let forstås ved hjælp af billedet tilføjet nedenfor,

I XY-planet, når vi bevæger os fra venstre mod højre langs x-aksen, øges x-koordinaten. På samme måde resulterer bevægelse fra bund til top langs y-aksen i en stigning i y-koordinaten. XY-planet er opdelt i fire kvadranter, hver med specifikke tegnkonventioner for x- og y-koordinater:
| Kvadrant | x-koordinat | y-koordinat |
|---|---|---|
| 1. kvadrant | Positiv (+) | Positiv (+) |
| 2. kvadrant | Negativ (-) | Positiv (+) |
| 3. kvadrant | Negativ (-) | Negativ (-) |
| 4. kvadrant | Positiv (+) | Negativ (-) |
Derfor har punkter i 1. kvadrant positive værdier for både x og y, dem i 2. kvadrant har negativ x og positiv y, 3. kvadrant har både negative x- og y-værdier, og 4. kvadrant har positiv x og et negativt y.
Plotte punkter på kvadranter
I et kartesisk plan identificeres punkter ved x-aksen og y-aksen. Disse punkter er betegnet som (a, b), hvor 'a' er x-koordinaten (abscisse), og 'b' er y-koordinaten (ordinaten). For at placere et punkt i en kvadrant overvejer vi tegnene på disse koordinater. Værdierne af x og y repræsenterer, hvor langt punktet er fra henholdsvis x-aksen og y-aksen.
Plot f.eks. punktet (2, -5) på det kartesiske plan. En analyse af koordinaternes fortegn afslører, at punktet er i 4. kvadrant. Det vil være 2 enheder væk fra x-aksen (til højre) og 5 enheder væk fra y-aksen (ned), ved at bruge origo som referencepunkt.
Trigonometriske værdier i forskellige kvadranter
Værdierne af forskellige trigonometriske funktioner i forskellige kvadranter kan læres ved at studere tabellen tilføjet nedenfor som,
| Kvadrant | Uden | Cos | Så | Cosecant | Sekant | Cotangens |
|---|---|---|---|---|---|---|
| 1. kvadrant | + | + | + | + | + | + |
| 2. kvadrant | + | – | + harald baldr | + | – | – |
| 3. kvadrant | – | – | – | – | – | + |
| 4. kvadrant bedste hentai | – | – | – | – | + | – |
I 1. kvadrant er alle trigonometriske forhold positive. I 2. kvadrant er Sinus og Cosecant positive (+), mens Cosinus og Secant er negative (-). I 3. kvadrant er Tangent og Cotangent positive (+), mens Cosinus og Secant er negative (-). I 4. kvadrant er Sinus og Cosecant negative (-), mens Cosinus og Secant er positive (+).
Læs mere,
- Koordinat geometri
- Parallelle linier
- Afstandsformel
Løste eksempler på kvadrant
Eksempel 1: Plot punktet A (3, -4) og identificer dets kvadrant.
Løsning:
Punkt A er placeret ved koordinaterne (3, -4). Da x-koordinaten er positiv (3) og y-koordinaten er negativ (-4), ligger punkt A i kvadrant IV.
Eksempel 2: Plot punktet P (-5, 2) og bestem dets kvadrant
Løsning:
Koordinaterne for punktet P er (-5, 2). For at bestemme kvadranten undersøger vi fortegnene for x- og y-koordinaterne.
X-koordinat er -5, hvilket indikerer en position til venstre for origo.
Y-koordinat er 2, hvilket indikerer en position over origo.
Da x-koordinaten er negativ og y-koordinaten er positiv, er punktet P placeret i kvadrant II.
Punkt P (-5, 2) er beliggende i kvadrant II af det kartesiske plan.
Øve problemer på kvadranter
Opgave 1: Plot punktet (1, -1) og identificer dets kvadrant.
Opgave 2: Find tre punkter på x-aksen og bestem deres kvadranter.
Opgave 3: Hvis et punkt ligger på y-aksen med koordinater (0, -3), hvilken kvadrant er det så i?
Opgave 4: Find punkterne Q (2, 2), R (-2, -2) og S (0, 0) og kontroller for kollinearitet.
Opgave 5: Plot punktet (-4, -3) og forklar, i hvilken kvadrant det er placeret.
Ofte stillede spørgsmål om kvadranter
1. Hvad er en kvadrant i matematik?
I matematik er en kvadrant en af de fire sektioner skabt af skæringspunktet mellem to vinkelrette linjer eller akser. Disse akser er typisk mærket som x-aksen og y-aksen i et kartesisk koordinatsystem.
2. Hvad kaldes skæringspunktet mellem to akser?
Skæringspunktet mellem to akser i et kartesisk koordinatsystem kaldes oprindelsen. Det er repræsenteret ved det punkt, hvor x-aksen og y-aksen mødes, normalt betegnet som (0,0).
3. Hvad er 4 kvadranter?
De fire kvadranter er sektionerne dannet ved at dele et kartesisk koordinatplan i fire lige store dele. De er mærket som første kvadrant (Q1), anden kvadrant (Q2), tredje kvadrant (Q3) og fjerde kvadrant (Q4).
4. Hvilken kvadrant er positiv?
Den positive kvadrant i et kartesisk koordinatsystem er den første kvadrant (Q1). I denne kvadrant er både x- og y-koordinaterne positive.
5. Hvad er brugen af kvadranter i grafer?
Kvadranter i grafer giver en systematisk måde at organisere og lokalisere punkter baseret på deres koordinater. De hjælper med at visualisere forhold mellem variabler og analysere mønstre i datasæt, hvilket gør det lettere at fortolke grafiske repræsentationer.
6. Hvilken kvadrant har begge værdierne for Koordinater Positive?
Den første kvadrant (Q1) er den kvadrant, hvor både x- og y-koordinaterne for punkter er positive. Det er den eneste kvadrant med begge positive værdier.
7. Hvad er de 4 kvadranter i en cirkel?
Begrebet kvadranter er ikke direkte anvendeligt på cirkler. I stedet opdeles cirkler i vinkler målt i grader. Men hvis man henviser til cirkulære sektorer, kan man bruge udtryk som første sektor, anden sektor, tredje sektor og fjerde sektor, svarende til forskellige vinkelområder.
