• Pushdown-automater er en måde at implementere en CFG på på samme måde, som vi designer DFA til en almindelig grammatik. En DFA kan huske en begrænset mængde information, men en PDA kan huske en uendelig mængde information.
• Pushdown-automater er simpelthen en NFA udvidet med en 'ekstern stack-hukommelse'. Tilføjelsen af ​​stak bruges til at give en last-in-first-out hukommelsesstyringsfunktion til Pushdown-automater. Pushdown-automater kan gemme en ubegrænset mængde information på stakken. Den kan få adgang til en begrænset mængde information på stakken. En PDA kan skubbe et element op på toppen af ​​stakken og springe et element af fra toppen af ​​stakken. For at læse et element ind i stakken, skal de øverste elementer springes af og gå tabt.
• En PDA er mere kraftfuld end FA. Ethvert sprog, der kan accepteres af FA, kan også accepteres af PDA. PDA accepterer også en sprogklasse, som ikke engang kan accepteres af FA. Således er PDA meget mere overlegen end FA.

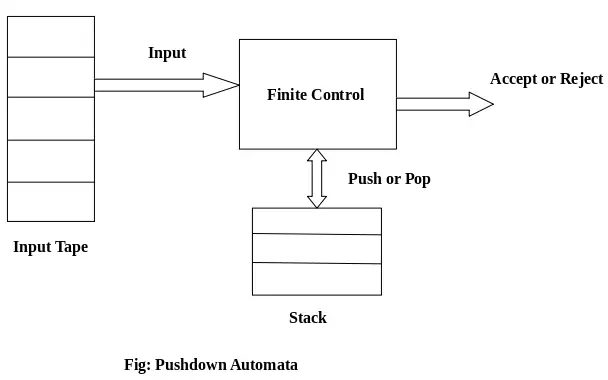
PDA-komponenter:

Indtastningsbånd: Indtastningsbåndet er opdelt i mange celler eller symboler. Indgangshovedet er skrivebeskyttet og må kun bevæge sig fra venstre mod højre, ét symbol ad gangen.

Endelig kontrol: Den endelige kontrol har en eller anden pointer, som peger på det aktuelle symbol, som skal læses.

Stak: Stakken er en struktur, hvori vi kun kan skubbe og fjerne emnerne fra den ene ende. Den har en uendelig størrelse. I PDA bruges stakken til at opbevare genstandene midlertidigt.

Formel definition af PDA:

PDA'en kan defineres som en samling af 7 komponenter:

Q: det endelige sæt af tilstande

∑: inputsættet

C: et staksymbol, som kan skubbes og springes fra stakken

q0: den oprindelige tilstand

primtal java

MED: et startsymbol, som er i Γ.

F: et sæt sluttilstande

d: kortlægningsfunktion, som bruges til at flytte fra nuværende tilstand til næste tilstand.

Øjeblikkelig beskrivelse (ID)

ID er en uformel notation af, hvordan en PDA beregner en inputstreng og træffer en beslutning om, at strengen accepteres eller afvises.

En øjeblikkelig beskrivelse er en tredobbelt (q, w, α), hvor:

q beskriver den aktuelle tilstand.

I beskriver det resterende input.

installering af brænder

-en beskriver stakens indhold, øverst til venstre.

Turnstile notation:

⊢-tegnet beskriver drejekorsets notation og repræsenterer ét træk.

⊢* tegnet beskriver en række træk.

For eksempel,

(p, b, T) ⊢ (q, w, α)

I ovenstående eksempel, mens man tager en overgang fra tilstand p til q, forbruges inputsymbolet 'b', og toppen af ​​stakken 'T' er repræsenteret af en ny streng α.

Eksempel 1:

Design en PDA til at acceptere et sprog aⁿb²ⁿ.

Løsning: På dette sprog skal n antal a'er efterfølges af 2n antal b'er. Derfor vil vi anvende en meget simpel logik, og det er, hvis vi læser enkelt 'a', vil vi skubbe to a'er på stakken. Så snart vi læser 'b', så for hver enkelt 'b' skulle der kun springes et 'a' fra stakken.

ID'et kan konstrueres som følger:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Når vi nu læser b, vil vi ændre tilstanden fra q0 til q1 og begynde at poppe tilsvarende 'a'. Derfor,

 δ(q0, b, a) = (q1, ε) 

Derfor vil denne proces med at poppe 'b' blive gentaget, medmindre alle symbolerne læses. Bemærk, at pop-handling kun forekommer i tilstand q1.

java 8

 δ(q1, b, a) = (q1, ε) 

Efter at have læst alle b'er, skulle alle de tilsvarende a'er blive poppet. Når vi læser ε som input-symbol, burde der derfor ikke være noget i stakken. Derfor bliver flytningen:

 δ(q1, ε, Z) = (q2, ε) 

Hvor

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

Vi kan opsummere ID'et som:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Nu vil vi simulere denne PDA for inputstrengen 'aaabbbbbb'.

10 af 50,00

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Eksempel 2:

Design en PDA til at acceptere et sprog 0ⁿ1^m0ⁿ.

Løsning: I denne PDA er n antal 0'ere efterfulgt af et hvilket som helst antal 1'er efterfulgt af n antal 0'er. Derfor vil logikken for design af en sådan PDA være som følger:

Skub alle 0'ere på stakken, når du møder de første 0'ere. Så hvis vi læser 1, så gør ingenting. Læs derefter 0, og for hver læsning af 0, pop en 0 fra stakken.

For eksempel:

Dette scenarie kan skrives i ID-formularen som:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Nu vil vi simulere denne PDA for inputstrengen '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT