Normalkraften er defineret som den kraft, som en overflade udøver på et andet objekt. Når et objekt er i hvile, er nettokraften, der udøves på det, lig med nul. En normal kraft kan ikke anvendes på to overflader, der ikke er forbundet med hinanden. Det kan tolkes som en komponent af kraften, der er lodret til enhver kontaktflade. Det bestemmer, hvor meget kraft kroppen afgiver til jorden. Normalkraften er kun lig med objektets vægt, hvis objektets hastighedsændring er negativ, hvilket betyder, at den decelererer.
Formel
Værdien af normalkraft afhænger af, hvor objektet er placeret i forhold til det andet objekt. Når en genstand skal falde, bestemmer den position, hvori objektet falder på jorden, værdien af normalkraften. Normalkraften er angivet med symbolet FN. Dens måleenhed er Newton (N), og dimensionsformlen er givet af [M1L1T-2].
Hvis et legeme hviler på en flad kraft, er normalkraften lig med værdien af gravitationsvægten, det vil sige mg.
F N = mg
hvor,
FNer normalkraften,
m er massen af hvilende objekt,
g er accelerationen på grund af tyngdekraften.
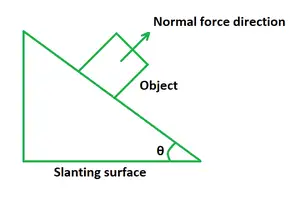
Hvis et legeme glider ned fra en skrå overflade i en vinkel, er værdien af normalkraften tyngdekraften tilføjet med en ekstra kraft af F sin θ. I dette tilfælde er normalkraften større end genstandens vægt.
F N = mg + F sin θ
Hvor,
FNer normalkraften,
m er massen af et glidende objekt,
g er accelerationen på grund af tyngdekraften,
θ er hældningsvinklen.
Hvis kraften virker på et legeme i opadgående retning, er værdien af normalkraft gravitationsvægten dekrementeret med en kraft af F sin θ. I dette tilfælde er nettonormalkraften mindre end genstandens vægt.
F N = mg – F sin θ
hvor,
... i javaFNer normalkraften,
m er massen af et glidende objekt,
g er accelerationen på grund af tyngdekraften,
θ er hældningsvinklen.
Hvis et legeme placeres på et skråplan, vil normalkraften FNer lig med produktet af gravitationsvægt og cosinus af hældningsvinklen.
F N = mg cos θ
hvor,
FNer normalkraften,
m er massen af et glidende objekt,
g er accelerationen på grund af tyngdekraften,
θ er hældningsvinklen.
Prøveproblemer
Opgave 1. En genstand med en masse på 2 kg hviler på et bord. Beregn den normale kraft, der udøves på den.
Løsning:
Vi har,
m = 2
g = 9,8
Ved at bruge formlen vi får,
FN= mg
= 2 (9,8)
= 19,6 N
Opgave 2. En genstand hviler på et bord med en kraft på 39,2 N. Beregn normalkraften, der udøves på den.
Løsning:
Vi har,
F = 39,2
g = 9,8
Ved at bruge formlen vi får,
FN= mg
=> m = F/g
=> m = 39,2/9,8
=> m = 4 kg
Opgave 3. En genstand med en masse på 10 kg glider ned med en kraft på 200 N fra en skrå overflade i en vinkel på 30°. Beregn den normale kraft, der udøves på den.
Løsning:
Vi har,
F = 200
m = 10
g = 9,8
θ = 30°
Ved at bruge formlen vi får,
FN= mg + F sin θ
= 10 (9,8) + 200 sin 30°
= 98 + 200 (1/2)
= 98 + 100
= 198 N
c# kode eksempler
Opgave 4. En genstand med massen 20 kg glider ned med en kraft på 400 N fra en skrå overflade i en vinkel på 30°. Beregn den normale kraft, der udøves på den.
Løsning:
Vi har,
F = 400
m = 20
g = 9,8
θ = 30°
Ved at bruge formlen vi får,
FN= mg + F sin θ
= 20 (9,8) + 400 sin 30°
= 196 + 400 (1/2)
= 196 + 200
= 396 N
Opgave 5. En genstand med en masse på 15 kg placeres på en skrå overflade i en vinkel på 30°. Beregn normalkraften, der udøves på den, hvis kraften virker opad med en værdi på 100 N.
Løsning:
Vi har,
F = 100
m = 15
g = 9,8
θ = 30°
Ved at bruge formlen vi får,
FN= mg – F sin θ
= 15 (9,8) – 100 uden 30°
= 147 – 100 (1/2)
= 147 – 50
= 97 N
Opgave 6. En genstand med en masse på 5 kg placeres på en skrå overflade i en vinkel på 60°. Beregn den normale kraft, der udøves på det på ethvert tidspunkt.
Løsning:
Vi har,
m = 5
g = 9,8
θ = 60°
Ved at bruge formlen vi får,
FN= mg cos θ
= 5 (9,8) (cos 60°)
= 49/2
= 24,5 N
Opgave 7. En genstand placeres på en skrå overflade i en vinkel på 60°. Beregn dens masse, hvis normalkraften, der udøves på den, er 400 N.
Løsning:
Vi har,
FN= 400,
θ = 60°
Ved at bruge formlen vi får,
FN= mg cos θ
m = F/(g cos θ)
= 400/ (9,8 × cos 60°)
skive java-array= 400/4,9
= 81,63 N
