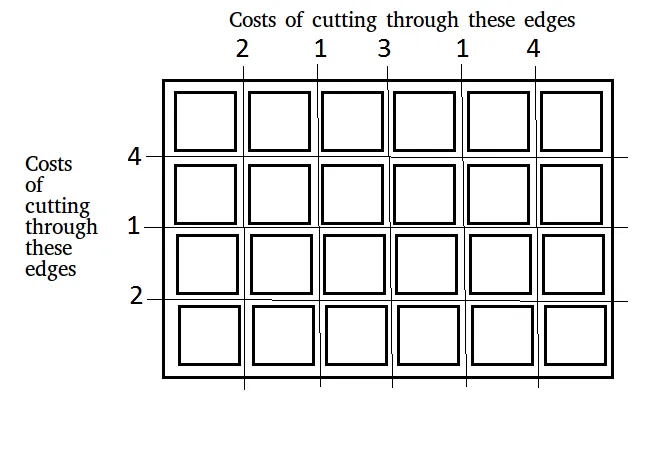
Givet en tavle af dimensioner n × m der skal skæres i n × m firkanter. Omkostningerne ved at lave et snit langs en vandret eller lodret kant er tilvejebragt i to arrays:

• x[] : Skæring af omkostninger langs de lodrette kanter (længdemæssigt).
• og[] : Skæring af omkostninger langs de vandrette kanter (breddemæssigt).

Find den minimale samlede omkostning, der kræves for at skære brættet i firkanter optimalt.

Eksempler: 

Input: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Produktion: 42
Forklaring:

I første omgang nej. af vandrette segmenter = 1 & nr. af lodrette segmenter = 1.
Den optimale måde at skære i firkanter er:
Vælg 4 (fra x) -> lodret klip Pris = 4 × vandrette segmenter = 4
 Nu vandrette segmenter = 1 lodrette segmenter = 2.
Vælg 4 (fra y) -> vandret klip Pris = 4 × lodrette segmenter = 8
 Nu vandrette segmenter = 2 lodrette segmenter = 2.
Vælg 3 (fra x) -> lodret klip Pris = 3 × vandrette segmenter = 6
 Nu vandrette segmenter = 2 lodrette segmenter = 3.
Vælg 2 (fra x) -> lodret klip Pris = 2 × vandrette segmenter = 4
 Nu vandrette segmenter = 2 lodrette segmenter = 4.
Vælg 2 (fra y) -> vandret klip Pris = 2 × lodrette segmenter = 8
 Nu vandrette segmenter = 3 lodrette segmenter = 4.
Vælg 1 (fra x) -> lodret klip Pris = 1 × vandrette segmenter = 3
Nu vandrette segmenter = 3 lodrette segmenter = 5.
Vælg 1 (fra x) -> lodret klip Pris = 1 × vandrette segmenter = 3
Nu vandrette segmenter = 3 lodrette segmenter = 6.
Vælg 1 (fra y) -> vandret klip Pris = 1 × lodrette segmenter = 6
Nu vandrette segmenter = 4 lodrette segmenter = 6.
Så de samlede omkostninger = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Input: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Produktion: 15
Forklaring:
I første omgang nej. af vandrette segmenter = 1 & nr. af lodrette segmenter = 1.
Den optimale måde at skære i firkanter er:
Vælg 1 (fra y) -> vandret klip Pris = 1 × lodrette segmenter = 1
Nu vandrette segmenter = 2 lodrette segmenter = 1.
Vælg 1 (fra y) -> vandret klip Pris = 1 × lodrette segmenter = 1
Nu vandrette segmenter = 3 lodrette segmenter = 1.
Vælg 1 (fra y) -> vandret klip Pris = 1 × lodrette segmenter = 1
Nu vandrette segmenter = 4 lodrette segmenter = 1.
Vælg 1 (fra x) -> lodret klip Pris = 1 × vandrette segmenter = 4
Nu vandrette segmenter = 4 lodrette segmenter = 2.
Vælg 1 (fra x) -> lodret klip Pris = 1 × vandrette segmenter = 4
Nu vandrette segmenter = 4 lodrette segmenter = 3.
Vælg 1 (fra x) -> lodret klip Pris = 1 × vandrette segmenter = 4
Nu vandrette segmenter = 4 lodrette segmenter = 4
Så de samlede omkostninger = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Indholdsfortegnelse

• [Naiv tilgang] Prøv alle permutationer - O((n+m)!×(n+m)) tid og O(n+m) rum
• [Forventet tilgang] Brug af grådig teknik - O( n (log n)+m (log m)) Tid og O(1) Mellemrum

[Naiv tilgang] Prøv alle permutationer - O((n+m)!×(n+m)) tid og O(n+m) rum

Ideen er at generere alle mulige permutationer af de givne nedskæringer og derefter beregne omkostningerne for hver permutation. Til sidst returnerer minimumsomkostningerne blandt dem.

Note: Denne tilgang er ikke mulig for større input, fordi antallet af permutationer vokser faktorielt som (m+n-2)!.
For hver permutation skal vi beregne omkostningerne i O(m+n) tid. Derfor bliver den samlede tidskompleksitet O((m+n−2)!×(m+n)).

[Forventet tilgang] Brug af grådig teknik - O( n (log n)+m (log m)) Tid og O(1) Mellemrum

Ideen er at lave de dyreste snit først ved hjælp af en grådig tilgang . Observationen er, at valget af den højeste omkostningsreduktion på hvert trin reducerer fremtidige omkostninger ved at påvirke flere stykker på én gang. Vi sorterer de lodrette (x) og vandrette (y) skæreomkostninger i faldende rækkefølge, og vælger derefter iterativt den største for at maksimere omkostningsbesparelser. De resterende snit behandles separat for at sikre, at alle sektioner er opdelt optimalt.

Hvad sker der, når vi laver et snit?

• Vandret snit → du skærer på tværs af bredden, så antallet af vandrette strimler øges (hCount++). Men prisen ganges med vCount (antallet af lodrette strimler), fordi det vandrette snit skal passere gennem alle lodrette segmenter.
• Lodret snit → du skærer på tværs af højden, så antallet af lodrette strimler øges (vCount++). Men prisen ganges med hCount (antallet af vandrette strimler), fordi det lodrette snit skal passere gennem alle vandrette segmenter.

Trin til at løse problemet:

• Sorter både x og y arrays i faldende rækkefølge.
• Brug to markører, én for x og en for y, startende fra den største værdi og bevæger sig mod mindre værdier.
• Vedligehold hCount og vCount for at spore, hvor mange segmenter hvert klip påvirker, og opdater dem i overensstemmelse hermed.
• Gentag, mens både x og y har ubehandlede nedskæringer, og vælg altid de højere omkostninger for at minimere de samlede udgifter.
• Hvis x har resterende klip, behandle dem med hCount multiplikator; behandle resterende y snit med vCount.
• Akkumuler samlede omkostninger ved hvert trin ved hjælp af formlen: skær omkostningerne * antal berørte stykker, hvilket sikrer minimale omkostninger.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42