- Vi har undersøgt de strategier, der kan ræsonnere enten frem eller tilbage, men en blanding af de to retninger er passende til at løse et komplekst og stort problem. En sådan blandet strategi gør det muligt, at man først løser hovedparten af et problem og derefter går tilbage og løser de små problemer, der opstår under kombinationen af de store dele af problemet. Sådan en teknik kaldes Middel-mål analyse .
- Means-Ends Analysis er problemløsningsteknikker, der bruges i kunstig intelligens til at begrænse søgning i AI-programmer.
- Det er en blanding af baglæns og fremad søgeteknik.
- MEA-teknikken blev først introduceret i 1961 af Allen Newell og Herbert A. Simon i deres problemløsende computerprogram, som blev navngivet som General Problem Solver (GPS).
- MEA-analyseprocessen var centreret om evalueringen af forskellen mellem den nuværende tilstand og måltilstand.
Sådan fungerer middel-mål-analyse:
Middel-mål-analyseprocessen kan anvendes rekursivt til et problem. Det er en strategi til at kontrollere søgning i problemløsning. Følgende er de vigtigste trin, som beskriver, hvordan MEA-teknikken fungerer til at løse et problem.
- Evaluer først forskellen mellem den oprindelige tilstand og den endelige tilstand.
- Vælg de forskellige operatorer, der kan anvendes for hver forskel.
- Anvend operatøren ved hver forskel, hvilket reducerer forskellen mellem den aktuelle tilstand og måltilstand.
Operatør Delmål
I MEA-processen opdager vi forskellene mellem den nuværende tilstand og måltilstand. Når disse forskelle opstår, kan vi anvende en operatør til at reducere forskellene. Men nogle gange er det muligt, at en operatør ikke kan anvendes til den aktuelle tilstand. Så vi skaber underproblemet i den nuværende tilstand, i hvilken operatør kan anvendes, en sådan type baglæns kæde, hvor operatører er udvalgt, og derefter delmål opstilles for at etablere forudsætningerne for operatøren kaldes Operatør Delmål .
konverter str til int
Algoritme for middel-mål-analyse:
Lad os tage Current state som CURRENT og Goal State som MÅL, så følger trinene til MEA-algoritmen.
- Vælg en ny operatør O, som er relevant for den aktuelle forskel, og hvis der ikke er en sådan operatør, signalér fejl.
- Forsøg at anvende operator O til CURRENT. Lav en beskrivelse af to tilstande.
i) O-Start, en tilstand, hvor O?s forudsætninger er opfyldt.
ii) O-Resultat, den tilstand, der ville resultere, hvis O blev anvendt i O-start. - Hvis
(Første del<------ mea (current, o-start)< strong>
Og
(SIDSTE DEL<----- mea (o-result, goal)< strong>, er vellykkede, signaler derefter Succes og returner resultatet af at kombinere FIRST-PART, O og LAST-PART.
Den ovenfor omtalte algoritme er mere egnet til et simpelt problem og ikke tilstrækkelig til at løse komplekse problemer.
Eksempel på middelværdianalyse:
Lad os tage et eksempel, hvor vi kender starttilstanden og måltilstanden som angivet nedenfor. I dette problem skal vi få måltilstanden ved at finde forskelle mellem starttilstanden og måltilstanden og anvende operatører.
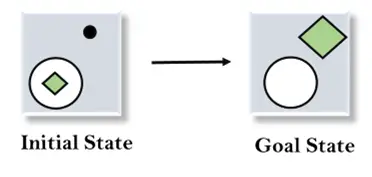
Løsning:
For at løse ovenstående problem vil vi først finde forskellene mellem begyndelsestilstande og måltilstande, og for hver forskel vil vi generere en ny tilstand og anvende operatørerne. De operatører, vi har til dette problem, er:
formatere en dato i java
1. Evaluering af den oprindelige tilstand: I det første trin vil vi evaluere starttilstanden og sammenligne starttilstanden og måltilstanden for at finde forskellene mellem begge tilstande.
vende strengen i java

2. Anvendelse af Slet-operatør: Da vi kan kontrollere, er den første forskel, at der i måltilstand ikke er noget priksymbol, som er til stede i starttilstanden, så først vil vi anvende Slet operatør for at fjerne denne prik.

3. Anvendelse af Move Operator: Efter anvendelse af Slet-operatoren opstår den nye tilstand, som vi igen vil sammenligne med måltilstand. Efter at have sammenlignet disse tilstande, er der en anden forskel, nemlig at kvadratet er uden for cirklen, så vi vil anvende Flyt operatør .

4. Anvendelse af Expand Operator: Nu genereres en ny tilstand i tredje trin, og vi vil sammenligne denne tilstand med måltilstanden. Efter at have sammenlignet staterne er der stadig en forskel, som er størrelsen på kvadratet, så vi vil anvende Udvid operatør , og til sidst vil den generere måltilstanden.

