Lineær regression og logistisk regression er de to berømte Machine Learning-algoritmer, der kommer under overvåget læringsteknik. Da begge algoritmer er af overvåget karakter, bruger disse algoritmer derfor mærket datasæt til at lave forudsigelserne. Men den største forskel mellem dem er, hvordan de bliver brugt. Den lineære regression bruges til at løse regressionsproblemer, mens logistisk regression bruges til at løse klassifikationsproblemerne. Beskrivelsen af begge algoritmer er givet nedenfor sammen med forskelstabellen.
Lineær regression:
- Lineær regression er en af de mest simple maskinlæringsalgoritmer, der kommer under Supervised Learning-teknik og bruges til at løse regressionsproblemer.
- Det bruges til at forudsige den kontinuerlige afhængige variabel ved hjælp af uafhængige variable.
- Målet med den lineære regression er at finde den bedste tilpasningslinje, der nøjagtigt kan forudsige outputtet for den kontinuerlige afhængige variabel.
- Hvis en enkelt uafhængig variabel bruges til forudsigelse, kaldes den simpel lineær regression, og hvis der er mere end to uafhængige variable, kaldes en sådan regression som multipel lineær regression.
- Ved at finde den bedste tilpasningslinje etablerer algoritmen forholdet mellem afhængig variabel og uafhængig variabel. Og forholdet bør være af lineær karakter.
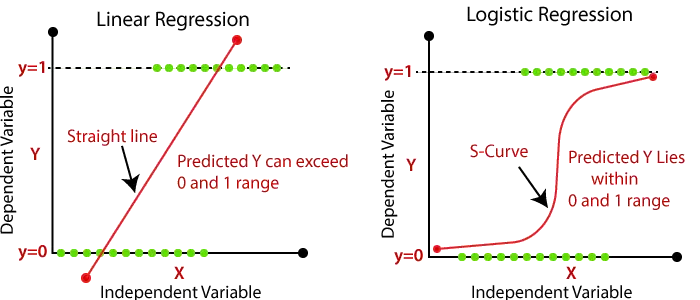
- Outputtet for lineær regression bør kun være de kontinuerlige værdier såsom pris, alder, løn osv. Forholdet mellem den afhængige variabel og den uafhængige variabel kan vises på billedet nedenfor:

I ovenstående billede er den afhængige variabel på Y-aksen (løn) og den uafhængige variabel er på x-aksen (erfaring). Regressionslinjen kan skrives som:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Hvor en0og en1er koefficienterne og ε er fejlleddet.
Logistisk regression:
- Logistisk regression er en af de mest populære Machine learning-algoritmer, der kommer under Supervised Learning-teknikker.
- Det kan bruges til klassifikation såvel som til regressionsproblemer, men bruges hovedsageligt til klassifikationsproblemer.
- Logistisk regression bruges til at forudsige den kategoriske afhængige variabel ved hjælp af uafhængige variable.
- Outputtet af logistisk regression-problem kan kun være mellem 0 og 1.
- Logistisk regression kan bruges, hvor sandsynligheden mellem to klasser er påkrævet. Såsom om det vil regne i dag eller ej, enten 0 eller 1, sandt eller falsk osv.
- Logistisk regression er baseret på konceptet Maximum Likelihood estimering. Ifølge denne vurdering skulle de observerede data være mest sandsynlige.
- I logistisk regression sender vi den vægtede sum af input gennem en aktiveringsfunktion, der kan kortlægge værdier mellem 0 og 1. En sådan aktiveringsfunktion er kendt som sigmoid funktion og den opnåede kurve kaldes sigmoid-kurve eller S-kurve. Overvej billedet nedenfor:

- Ligningen for logistisk regression er:

Forskellen mellem lineær regression og logistisk regression:
| Lineær regression | Logistisk regression |
|---|---|
| Lineær regression bruges til at forudsige den kontinuerlige afhængige variabel ved hjælp af et givet sæt af uafhængige variable. | Logistisk regression bruges til at forudsige den kategoriske afhængige variabel ved hjælp af et givet sæt af uafhængige variable. |
| Lineær regression bruges til at løse et regressionsproblem. | Logistisk regression bruges til at løse klassifikationsproblemer. |
| I lineær regression forudsiger vi værdien af kontinuerte variable. | I logistisk regression forudsiger vi værdierne af kategoriske variable. |
| Ved lineær regression finder vi den bedste tilpasningslinje, hvorved vi nemt kan forudsige outputtet. | I logistisk regression finder vi S-kurven, hvormed vi kan klassificere prøverne. |
| Mindste kvadratisk estimeringsmetode bruges til estimering af nøjagtighed. | Maksimal sandsynlighed estimering metode bruges til estimering af nøjagtighed. |
| Outputtet for lineær regression skal være en kontinuerlig værdi, såsom pris, alder osv. | Outputtet af logistisk regression skal være en kategorisk værdi såsom 0 eller 1, Ja eller Nej osv. |
| Ved lineær regression kræves det, at forholdet mellem afhængig variabel og uafhængig variabel skal være lineær. | I logistisk regression er det ikke nødvendigt at have den lineære sammenhæng mellem den afhængige og uafhængige variabel. |
| Ved lineær regression kan der være kollinearitet mellem de uafhængige variable. | Ved logistisk regression bør der ikke være kolinearitet mellem den uafhængige variabel. |
