Længde, bredde og højde er dimensionerne af en geometrisk figur, som angiver hvor lang, hvor bred og hvor høj figuren er. Længde, bredde og højde er vigtige værktøjer til geometriske figurer.
I denne artikel lærer du alle detaljer relateret til længde, bredde og højde. Hvis du er en ægte studerende og nysgerrig efter at vide om længde, bredde og højde, så er du på det rigtige sted.
Indholdsfortegnelse
- Hvad er Længde Bredde Højde?
- Sådan skriver du dimensioner af længde og bredde
- Længde×Bredde×Højde
- Længde vs bredde
- Længde, bredde og højde i rektangel
- Længde Bredde Højde Formel
Hvad er Længde Bredde Højde?
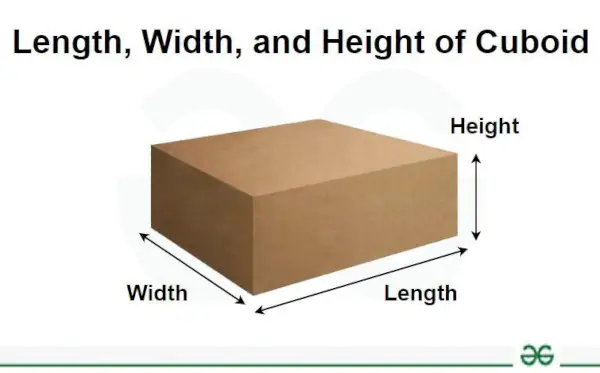
Længde, bredde og højde bruges til at finde siden eller dimensionerne af et objekt. En figurs længste side er længde, bredde er den korteste side af en figur og figurens lodrette dimension kaldes højde. Længde og bredde bruges i todimensionelle former (2D-former), hvorimod vi i tredimensionelle former (3D-former) bruger højden sammen med længden og bredden.
Længde
Værktøj, der kræver måling af afstand mellem to punkter, er kendt som længde. Længde bruges til at måle den længste dimension af en figur. Længde er en lineær måling, som kun bruges til at måle afstanden, der adskiller to punkter. Længdeenhederne er meter, kilometer, centimeter, tommer og så videre.
Som et eksempel på længde kan vi sige, at længden af banen på en cricketbane er 20 meter lang.
Bredde
Værktøj, der bruges til at måle den kortere afstand af et objekt eller en figur, kaldes Width. Det er den kortere dimension af en figur. Bredde er en lineær måling, som kun bruges til at måle den kortere afstand af et objekt. Enhederne for bredde er meter, kilometer, centimeter, tommer og så videre.
Som et eksempel på bredden kan vi sige, at bredden af banen på en cricketbane er 5 meter lang.
Højde
Et andet udtryk for højde er dybde. Højde eller dybde er den tredje lodrette dimension af objektet i 3D-form. Den identificerer, hvor dyb eller høj et objekt er. Højdeenheder er meter, kilometer, centimeter, tommer og så videre.
Sådan skriver du dimensioner af længde og bredde
Dimensioner af længde, bredde og højde kan meget nemt skrives, da vi allerede har læst definitionen af disse værktøjer. I en 2D geometrisk form får vi kun to dimensioner, en længde og en bredde (bredde). I en 3D-form får vi alle tre dimensioner af længde, bredde og højde. Den længste side af figuren er mærket som længden. Den lodrette dimension skrives som højden eller dybden. Den resterende side kaldes bredde eller bredde.
Dette koncept er vist i ovenstående diagram. Enheder af disse dimensioner er udtrykt i enheder som meter, centimeter, tommer og så videre.
Længde×Bredde×Højde
Når alle de tre dimensioner ganges sammen, får vi volumen af en geometrisk form. Volumen er defineret som mængden af plads optaget af en geometrisk form. Det rumfanget af en kuboid er lig med multiplikationen af dens længde, bredde og højde. Med andre ord, hvis vi multiplicerer alle tre dimensioner sammen, får vi rumfanget af en kuboid eller en hvilken som helst rektangulær kasse.
forberede sig til test mockito
Matematisk, volumen af et rektangulært prisme ( cuboid ) eller en æske = Længde × Bredde × Højde.
For eksempel, hvis længden, bredden og højden af et rektangulært prisme er henholdsvis 5, 8 og 10 enheder, så er dets volumen (V)
V = 5 × 8 × 10
V = 400 terningsenheder
Længde vs bredde
Længde og bredde bruges begge til at måle afstand eller dimension af en side, men der er en bemærkelsesværdig forskel mellem disse to. Længde er den længste dimension, mens bredde er den korteste dimension. Længden er altid større end bredden. Med andre ord, længde angiver en figurs længere side, mens bredde angiver dens kortere side. Bredde (bredde) giver den brede karakter af en geometrisk form, mens længden fortæller, hvor lang en form er.
Hvis der gives to mål af en geometrisk form, som er henholdsvis 100 cm og 70 cm, så kan vi sagtens sige, at 100 cm er længden og 70 cm er bredden.
Længde, bredde og højde i rektangel
Et rektangel er et eksempel på 2D-form, så det har kun længde og bredde, men en rektangulær kasse eller et rektangulært prisme (kuboid) er 3D-form, så det har alle tre dimensioner: længde, bredde og højde. Så vi kan sige, at forlængelser af rektangulær form i 3D indeholder længde, bredde og højde.
Længde Bredde Højde Formel
Længde, Bredde og Højde bruges til at beregne volumen og overfladeareal af et rektangulært prisme ved hjælp af visse formler. Disse formler er givet nedenfor,
Volumen af rektangulært prisme Formel
arv i c++
Volumen af rektangulære prisme = længde × bredde × højde
Overfladeareal af rektangulært prisme Formel
Lateral overfladeareal af rektangulært prisme = 2 [(længde × bredde) + (bredde × højde)]
Total overfladeareal af rektangulært prisme = 2 [(længde × bredde) + (bredde × højde) + (længde × højde)]
Længde Bredde Højde af en kasse
Længde, bredde og højde af en kasse kan nemt udtrykkes ved at se på dens form. Fordi vi ved, at længden af kassen generelt er den længste side, er dens bredde den kortere side, og dens højde er dimension i lodret dimension.

Generelt for alle 3D-former skrives dimensioner som Længde, efterfulgt af Bredde eller Bredde og Højde. Det betyder, at hvis en kasses dimensioner skal måles, så skal det angives som længde, bredde og højde. For eksempel angiver 10 meter, 5 meter og 8 meter,
- Længde på kasse = 10 meter
- Kassens bredde = 5 meter
- Kassens højde = 8 meter
Lignende artikler,
- Område med 2D-former
- Overfladeareal og volumen af 3D-former
Længde Bredde Højde Eksempler
Nogle eksempler på emnet længde, bredde og højde er,
Eksempel 1: Dimensioner af en 2D rektangelhave er 50 meter og 35 meter. Hvad er dimensionen af længden og bredden?
Løsning:
Som vi ved,
Længere dimension betragtes generelt som længde og kortere er bredde
Dimension af længde er 50 meter og bredde er 35 meter
Eksempel 2: Hvis dimensionerne af en rektangulær kasse er henholdsvis 26 m, 22 m og 24 m. Hvad bliver værdien af højden af denne rektangulære kasse?
Løsning:
Som vi ved, er dimensioner i en 3D-form udtrykt i rækkefølge efter længde, bredde og højde.
Givet dimensioner,
- Længde = 26 m
- Bredde = 22 m
- Højde = 24 m
Så højden er 24 meter
Eksempel 3: Længde, bredde og højde af et rektangulært prisme er angivet som 6 cm, 4 cm og 5 cm. Bestem dens volumen.
Løsning:
givet,
- Længde = 6 cm
- Bredde = 4 cm
- Højde = 5 cm
Volumen = længde × bredde × højde
Volumen = 6 × 4 × 5
Volumen = 120 cm³
Øvelsesspørgsmål om Længde Bredde Højde
Nogle øvelsesspørgsmål om længde, bredde og højde er,
Q1: Find rumfanget af en kasse med længde, bredde og højde som længde = 12 cm, bredde = 8 cm, højde = 4 cm.
Q2: Find volumen af en kasse med længde, bredde og højde som længde = 18 m, bredde = 9 m, højde = 3 m.
Spørgsmål 3: Find TSA for en kasse med længde, bredde og højde som længde = 42 cm, bredde = 28 cm, højde = 14 cm.
Spørgsmål 4: Find LSA for en kasse med længde, bredde og højde som længde = 7 cm, bredde = 5 cm, højde = 6 cm.
Ofte stillede spørgsmål om længde og bredde
Hvad er Længde Bredde Højde?
Længde, Bredde og Højde er de værktøjer, der bruges til at måle dimensioner af forskellige 3-d objekter.
ipconfig til ubuntu
Hvad er den længste dimension mellem bredde og længde?
Længden er længere dimension. Længde bruges generelt til måling af længere dimensioner af et objekt.
Hvad sker der med dimension, hvis objektet er rundt, som en bold?
Til forskellige mål for objekter som bolde bruger vi radius eller diameter i stedet for længde, bredde eller højde, hvis objektet er rundt. 'Højden' af en kugle er lig med dens diameter.
Er volumen altid beregnet efter formellængde × bredde × højde?
Formel for volumen er generelt længde × bredde × højde for 3D-former, hvor dens dimensioner er, længde, bredde og højde.
