Vi har set forskellige metoder med forskellige tidskompleksiteter til at beregne LCA i n-ært træ:-
Metode 1: Naiv metode (ved at beregne rod til node-sti) | O(n) pr. forespørgsel
Metode 2: Brug af Sqrt-nedbrydning | O(sqrt H)
Metode 3: Brug af Sparse Matrix DP-tilgang | O(logn)
Lad os studere en anden metode, der har hurtigere forespørgselstid end alle ovenstående metoder. Så vores mål vil være at beregne LCA i konstant tid ~ O(1) . Lad os se, hvordan vi kan opnå det.
Metode 4: Brug af Range Minimum Query
Vi har diskuteret LCA og RMQ for binært træ . Her diskuterer vi LCA-problem til RMQ-problemkonvertering for n-ært træ.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Nøglekoncept: I denne metode vil vi reducere vores LCA-problem til RMQ(Range Minimum Query)-problem over et statisk array. Når vi har gjort det, relaterer vi minimumsforespørgslerne til rækkevidde til de påkrævede LCA-forespørgsler.
Det første trin vil være at nedbryde træet til et fladt lineært array. For at gøre dette kan vi anvende Euler-vandringen. Euler-vandringen vil give forudbestillingsgennemgangen af grafen. Så vi vil udføre en Euler Walk på træet og gemme noderne i et array, når vi besøger dem. Denne proces reducerer træet > 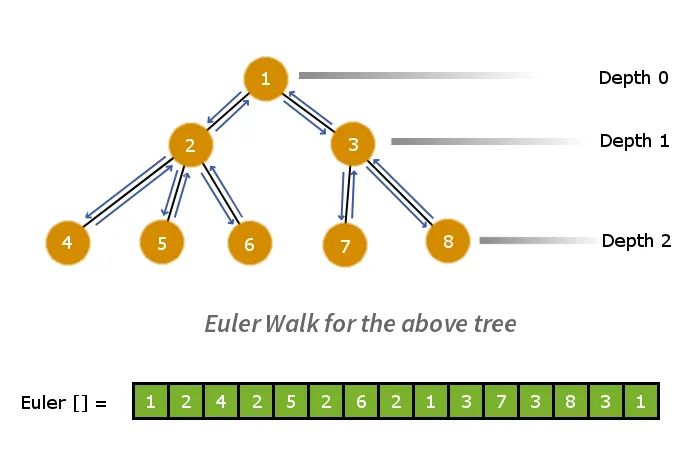
Lad os nu tænke i generelle vendinger: Overvej alle to noder på træet. Der vil være nøjagtig én sti, der forbinder både noderne, og den node, der har den mindste dybdeværdi i stien, vil være LCA for de to givne noder.
Tag nu en hvilken som helst to forskellige noder sige i og v i Euler walk array. Nu vil alle elementerne i stien fra u til v ligge mellem indekset for knudepunkter u og v i Euler walk-arrayet. Derfor skal vi blot beregne noden med den mindste dybde mellem indekset for node u og node v i euler-arrayet.
Til dette vil vi vedligeholde et andet array, der vil indeholde dybden af alle noderne svarende til deres position i Euler walk-arrayet, så vi kan anvende vores RMQ-algoritme på det.
Nedenstående er euler walk-arrayet parallelt med dets dybdesporarray.

python rstrip
Eksempel: - Overvej to noder node 6 og node 7 i Euler-arrayet. For at beregne LCA for node 6 og node 7 ser vi på den mindste dybdeværdi for alle noderne mellem node 6 og node 7.
Derfor node 1 har den mindste dybdeværdi = 0 og derfor er det LCA for node 6 og node 7.

Implementering:-
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
Euler Path og Depth array er de samme som beskrevet ovenfor
sorter array liste
Indeks for første optræden FAI[] : First Appearance index Array vil gemme indekset for den første position af hver node i Euler Path arrayet. FAI[i] = Første optræden af ith node i Euler Walk-array.
Implementeringen af ovenstående metode er angivet nedenfor:-
Implementering:
C++// C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std; #define sz 101 vector < int > adj[sz]; // stores the tree vector < int > euler; // tracks the eulerwalk vector < int > depthArr; // depth for each node corresponding // to eulerwalk int FAI[sz]; // stores first appearance index of every node int level[sz]; // stores depth for all nodes in the tree int ptr; // pointer to euler walk int dp[sz][18]; // sparse table int logn[sz]; // stores log values int p2[20]; // stores power of 2 void buildSparseTable(int n) { // initializing sparse table memset(dp-1sizeof(dp)); // filling base case values for (int i=1; i<n; i++) dp[i-1][0] = (depthArr[i]>depthArr[i-1])?i-1:i; // dp to fill sparse table for (int l=1; l<15; l++) for (int i=0; i<n; i++) if (dp[i][l-1]!=-1 and dp[i+p2[l-1]][l-1]!=-1) dp[i][l] = (depthArr[dp[i][l-1]]>depthArr[dp[i+p2[l-1]][l-1]])? dp[i+p2[l-1]][l-1] : dp[i][l-1]; else break; } int query(int lint r) { int d = r-l; int dx = logn[d]; if (l==r) return l; if (depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]) return dp[r-p2[dx]][dx]; else return dp[l][dx]; } void preprocess() { // memorizing powers of 2 p2[0] = 1; for (int i=1; i<18; i++) p2[i] = p2[i-1]*2; // memorizing all log(n) values int val = 1ptr=0; for (int i=1; i<sz; i++) { logn[i] = ptr-1; if (val==i) { val*=2; logn[i] = ptr; ptr++; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs(int curint prevint dep) { // marking FAI for cur node if (FAI[cur]==-1) FAI[cur] = ptr; level[cur] = dep; // pushing root to euler walk euler.push_back(cur); // incrementing euler walk pointer ptr++; for (auto x:adj[cur]) { if (x != prev) { dfs(xcurdep+1); // pushing cur again in backtrack // of euler walk euler.push_back(cur); // increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr() { for (auto x : euler) depthArr.push_back(level[x]); } int LCA(int uint v) { // trivial case if (u==v) return u; if (FAI[u] > FAI[v]) swap(uv); // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } void addEdge(int uint v) { adj[u].push_back(v); adj[v].push_back(u); } int main(int argc char const *argv[]) { // constructing the described tree int numberOfNodes = 8; addEdge(12); addEdge(13); addEdge(24); addEdge(25); addEdge(26); addEdge(37); addEdge(38); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; memset(FAI-1sizeof(FAI)); dfs(100); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.size()); cout << 'LCA(67) : ' << LCA(67) << 'n'; cout << 'LCA(64) : ' << LCA(64) << 'n'; return 0; }
// Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList; import java.util.Arrays; class GFG{ static int sz = 101; @SuppressWarnings('unchecked') // Stores the tree static ArrayList<Integer>[] adj = new ArrayList[sz]; // Tracks the eulerwalk static ArrayList<Integer> euler = new ArrayList<>(); // Depth for each node corresponding static ArrayList<Integer> depthArr = new ArrayList<>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[][] dp = new int[sz][18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[i][j] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 1][0] = (depthArr.get(i) > depthArr.get(i - 1)) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[i][l - 1] != -1 && dp[i + p2[l - 1]][l - 1] != -1) dp[i][l] = (depthArr.get(dp[i][l - 1]) > depthArr.get( dp[i + p2[l - 1]][l - 1])) ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr.get(dp[l][dx]) > depthArr.get(dp[r - p2[dx]][dx])) return dp[r - p2[dx]][dx]; else return dp[l][dx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.add(cur); // Incrementing euler walk pointer ptr++; for(Integer x : adj[cur]) { if (x != prev) { dfs(x cur dep + 1); // Pushing cur again in backtrack // of euler walk euler.add(cur); // Increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { for(Integer x : euler) depthArr.add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler.get(query(FAI[u] FAI[v])); } static void addEdge(int u int v) { adj[u].add(v); adj[v].add(u); } // Driver code public static void main(String[] args) { for(int i = 0; i < sz; i++) { adj[i] = new ArrayList<>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Arrays.fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.size()); System.out.println('LCA(67) : ' + LCA(6 7)); System.out.println('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by sanjeev2552
# Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range(101)] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [-1] * 101 # stores depth for all nodes in the tree level = [0] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[-1] * 18 for _ in range(101)] # stores log values logn = [0] * 101 # stores power of 2 p2 = [0] * 20 def buildSparseTable(n: int): # initializing sparse table for i in range(n): dp[i][0] = i-1 if depthArr[i] > depthArr[i-1] else i # dp to fill sparse table for l in range(1 15): for i in range(n): if dp[i][l-1] != -1 and dp[i+p2[l-1]][l-1] != -1: dp[i][l] = dp[i+p2[l-1]][l-1] if depthArr[dp[i][l-1] ] > depthArr[dp[i+p2[l-1]][l-1]] else dp[i][l-1] else: break def query(l: int r: int) -> int: d = r-l dx = logn[d] if l == r: return l if depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]: return dp[r-p2[dx]][dx] else: return dp[l][dx] def preprocess(): global ptr # memorizing powers of 2 p2[0] = 1 for i in range(1 18): p2[i] = p2[i-1]*2 # memorizing all log(n) values val = 1 ptr = 0 for i in range(1 101): logn[i] = ptr-1 if val == i: val *= 2 logn[i] = ptr ptr += 1 def dfs(cur: int prev: int dep: int): global ptr # marking FAI for cur node if FAI[cur] == -1: FAI[cur] = ptr level[cur] = dep # pushing root to euler walk euler.append(cur) # incrementing euler walk pointer ptr += 1 for x in adj[cur]: if x != prev: dfs(x cur dep+1) # pushing cur again in backtrack # of euler walk euler.append(cur) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr(): global depthArr for x in euler: depthArr.append(level[x]) def LCA(u: int v: int) -> int: # trivial case if u == v: return u if FAI[u] > FAI[v]: u v = v u # doing RMQ in the required range return euler[query(FAI[u] FAI[v])] def addEdge(u v): adj[u].append(v) adj[v].append(u) # constructing the described tree numberOfNodes = 8 addEdge(1 2) addEdge(1 3) addEdge(2 4) addEdge(2 5) addEdge(2 6) addEdge(3 7) addEdge(3 8) # performing required precalculations preprocess() # doing the Euler walk ptr = 0 FAI = [-1] * (numberOfNodes + 1) dfs(1 0 0) # creating depthArray corresponding to euler[] makeArr() # building sparse table buildSparseTable(len(depthArr)) print('LCA(67) : ' LCA(6 7)) print('LCA(64) : ' LCA(6 4))
// C# program to demonstrate LCA of n-ary // tree in constant time. using System; using System.Collections.Generic; public class GFG { static int sz = 101; // Stores the tree static List<int>[] adj = new List<int>[sz]; // Tracks the eulerwalk static List<int> euler = new List<int>(); // Depth for each node corresponding static List<int> depthArr = new List<int>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[] dp = new int[sz 18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[ij] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 10] = (depthArr[i] > depthArr[i - 1]) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[il - 1] != -1 && dp[i + p2[l - 1]l - 1] != -1) dp[il] = (depthArr[dp[il - 1]] > depthArr[dp[i + p2[l - 1]l - 1]]) ? dp[i + p2[l - 1]l - 1] : dp[il - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr[dp[ldx]] > depthArr[dp[r - p2[dx]dx]]) return dp[r - p2[dx]dx]; else return dp[ldx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.Add(cur); // Incrementing euler walk pointer ptr++; foreach (int x in adj[cur]) { if (x != prev) { dfs(x cur dep + 1); euler.Add(cur); ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { foreach (int x in euler) depthArr.Add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } static void addEdge(int u int v) { adj[u].Add(v); adj[v].Add(u); } // Driver Code static void Main(string[] args) { int sz = 9; adj = new List<int>[sz]; for (int i = 0; i < sz; i++) { adj[i] = new List<int>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Array.Fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.Count); Console.WriteLine('LCA(67) : ' + LCA(6 7)); Console.WriteLine('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by Prince Kumar
let adj = []; for (let _ = 0; _ < 101; _++) { adj.push([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array(101).fill(-1); // stores depth for all nodes in the tree let level = new Array(101).fill(0); // pointer to euler walk let ptr = 0; // sparse table let dp = []; for (let _ = 0; _ < 101; _++) { dp.push(new Array(18).fill(-1)); } // stores log values let logn = new Array(101).fill(0); // stores power of 2 let p2 = new Array(20).fill(0); function buildSparseTable(n) { // initializing sparse table for (let i = 0; i < n; i++) { dp[i][0] = i - 1 >= 0 && depthArr[i] > depthArr[i - 1] ? i - 1 : i; } // dp to fill sparse table for (let l = 1; l < 15; l++) { for (let i = 0; i < n; i++) { if ( dp[i][l - 1] !== -1 && dp[i + p2[l - 1]][l - 1] !== -1 ) { dp[i][l] = depthArr[dp[i][l - 1]] > depthArr[dp[i + p2[l - 1]][l - 1]] ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; } else { break; } } } } function query(l r) { let d = r - l; let dx = logn[d]; if (l === r) { return l; } if (depthArr[dp[l][dx]] > depthArr[dp[r - p2[dx]][dx]]) { return dp[r - p2[dx]][dx]; } else { return dp[l][dx]; } } function preprocess() { // memorizing powers of 2 p2[0] = 1; for (let i = 1; i < 18; i++) { p2[i] = p2[i - 1] * 2; } // memorizing all log(n) values let val = 1; ptr = 0; for (let i = 1; i < 101; i++) { logn[i] = ptr - 1; if (val === i) { val *= 2; logn[i] = ptr; ptr += 1; } } } function dfs(cur prev dep) { // marking FAI for cur node if (FAI[cur] === -1) { FAI[cur] = ptr; } level[cur] = dep; // pushing root to euler walk euler.push(cur); // incrementing euler walk pointer ptr += 1; for (let x of adj[cur]) { if (x !== prev) { dfs(x cur dep + 1); // pushing cur again in backtrack // of euler walk euler.push(cur); // increment euler walk pointer ptr += 1; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr() { for (let x of euler) { depthArr.push(level[x]); } } function LCA(u v) { // trivial case if (u === v) { return u; } if (FAI[u] > FAI[v]) { [u v] = [v u]; } // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } function addEdge(u v) { adj[u].push(v); adj[v].push(u); } // constructing the described tree let numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; FAI = new Array(numberOfNodes + 1).fill(-1); dfs(1 0 0); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.length); console.log('LCA(67) : ' LCA(6 7)); console.log('LCA(64) : ' LCA(6 4));
Produktion
LCA(67) : 1 LCA(64) : 2
Bemærk: Vi forudberegner al den nødvendige effekt af 2'er og forudberegner også alle de nødvendige logværdier for at sikre konstant tidskompleksitet pr. forespørgsel. Hvis vi ellers lavede logberegning for hver forespørgselsoperation, ville vores tidskompleksitet ikke have været konstant.
Tidskompleksitet: Konverteringsprocessen fra LCA til RMQ udføres af Euler Walk, der tager På) tid.
Forbehandling af den sparsomme tabel i RMQ tager O(nlogn) tid, og besvarelsen af hver forespørgsel er en konstant tidsproces. Derfor er den overordnede tidskompleksitet O(nlogn) - forbehandling og O(1) for hver forespørgsel.
Hjælpeplads: O(n+s)
Opret quiz
