Trekanter er tresidede lukkede polygoner dannet af skæringspunktet mellem tre linjer. Det støder man meget på i hverdagen. Det er en af ​​de grundlæggende former for geometri. Den har tre sider, tre vinkler og tre spidser. En retvinklet trekant er en, hvor en af ​​vinklerne altid er lig med 90°. Pythagoras sætning er afledt for retvinklede trekanter, som angiver, at kvadratet af hypotenusen (den længste side) er lig med summen af ​​kvadraterne af grund og vinkelret.

Givet længden af ​​mindst to sider af en retvinklet trekant, kan vi finde værdien af ​​enhver vinkel i den retvinklede trekant. Til dette bruger vi forskellige trigonometriske funktioner som sinus, cosinus, tangens, cotangens, sek og cosec. Disse hjælper os med at relatere vinklerne i en retvinklet trekant til dens sider.

Ejendomme

• Der er et retvinklet toppunkt blandt de tre toppunkter
• Siden modsat det retvinklede toppunkt kaldes hypotenusen .
• Længden af ​​siderne følger Pythagoras sætning, som siger

hypotenusen ² = base ² + højde ²

• Hypotenusen er den længste side af en retvinklet trekant.
• De andre vinkler end den rette vinkel er spidse vinkler, da værdien er mindre end 90^O

Trigonometriske funktioner

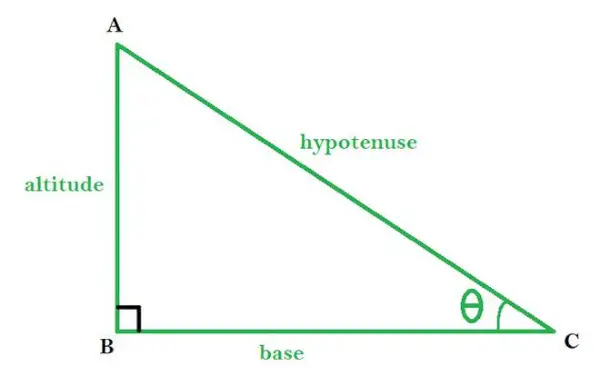
ABC er en retvinklet trekant med ∠B som retvinklet

simpelt python-program

• cosθ: Dette giver forholdet mellem basen ved hypotenusen af ​​en retvinklet trekant.

cosθ = base / hypotenuse

• syndθ: Dette giver forholdet mellem højde ved hypotenusen af ​​en retvinklet trekant.

sinθ = højde / hypotenuse

• tanθ: Det er forholdet mellem højde og bunden af ​​en retvinklet trekant.

tanθ = højde / base

• barneseng θ: Det er det omvendte af tanθ
• sekθ: Det er det omvendte af cosθ
• cosecθ: Det er det omvendte af sinθ

For at finde vinklerne i en retvinklet trekant kan vi tage den trigonometriske inverse af forholdet mellem givne sider i trekanten.

Eksempel:

Hvis sinθ = x, så kan vi skrive

θ = synd ^-1 x.

Dette returnerer den vinkel, for hvilken vinklens sinusværdi er x.

Tilsvarende findes der cos^-1θ, altså^-1jeg, barneseng^-1θ, sek^-1θ og cosec^-1jeg

Prøveproblemer

Spørgsmål 1. Givet en retvinklet trekant, hvor grundfladen er lig med 10 cm og hypotenusen er lig med 20 cm. Find værdien af ​​grundvinklen.

Løsning:

Givet, base = 10 cm

Hypotenus = 20 cm

Lad, værdien af ​​grundvinklen være θ. Vi kan skrive

cosθ = base / hypotenuse = 10/20 = 1/2

θ = cos^-1(1/2) = 60^O

Værdien af ​​grundvinklen er således 60 ^O .

Spørgsmål 2. Find værdien af ​​vinkler i en retvinklet trekant, givet at en af ​​de spidse vinkler er det dobbelte af den anden.

Løsning:

Da vi kender summen af ​​alle tre vinkler i en trekant er 180^O.

Da en af ​​vinklerne er 90^Oog en af ​​de spidse vinkler er det dobbelte af den anden, kan vi betragte dem som θ og 2θ.

Så vi kan skrive

90^O+ θ + 2θ = 180^O

3θ = 180^O– 90^O

3θ = 90^O

θ = 90^O/3 = 30 ^O

2θ = 2 × 30^O= 60 ^O

Så vinklerne er 30 ^O , 60 ^O , og 90 ^O .

Spørgsmål 3. Find værdien af ​​højdevinklen for en stige med en længde på 5m, givet at stigens basis er i en afstand af 3m fra væggen.

Løsning:

Da stigen fungerer som hypotenusen af ​​en retvinklet trekant og grundafstanden er lig med 3m, kan vi skrive

Hypotenus = 5m

Base = 3m

Lad højdevinklen være θ. Så kan vi skrive

cosθ = Base / Hypotenuse = 3/5

θ = cos^-1(3/5)

θ = 53^O

Således er værdien af ​​højdevinklen 53^O.

Spørgsmål 4. Find værdien af ​​hypotenusen, givet længden af ​​højden er 8m og grundvinklen er lig med 30 ^O .

Løsning:

Givet er grundvinklen lig med 30^Oog højde er lig med 8m, kan vi anvende sinusfunktionen til at finde længden af ​​hypotenusen.

synd 30 ^O = højde / hypotenuse

hypotenuse = højde / sind30^O

Siden værdien af ​​sin30^Oer lig med 1/2, kan vi skrive

hypotenuse = højde / (1/2) = 2 × højde

Således er hypotenusen = 2 × 8 = 16m

Således er længden af ​​hypotenusen lig med 16m.