• Hill climbing algoritme er en lokal søgealgoritme, som kontinuerligt bevæger sig i retning af stigende højde/værdi for at finde toppen af ​​bjerget eller den bedste løsning på problemet. Den afsluttes, når den når en spidsværdi, hvor ingen nabo har en højere værdi.
• Bakkebestigningsalgoritme er en teknik, som bruges til at optimere de matematiske problemer. Et af de meget diskuterede eksempler på bakkeklatringsalgoritme er Traveling-salesman Problem, hvor vi skal minimere den afstand, som sælgeren tilbagelægger.
• Den kaldes også grådig lokalsøgning, da den kun ser til sin gode umiddelbare nabostat og ikke længere end det.
• En node af bakkeklatring algoritme har to komponenter, som er tilstand og værdi.
• Bakkeklatring bruges mest, når en god heuristik er tilgængelig.
• I denne algoritme behøver vi ikke at vedligeholde og håndtere søgetræet eller grafen, da den kun beholder en enkelt aktuel tilstand.

Funktioner ved bakkeklatring:

Følgende er nogle hovedtræk ved Hill Climbing Algorithm:

Generer og test variant:Hill Climbing er varianten af ​​Generate and Test-metoden. Generer og test metoden producerer feedback, som hjælper med at beslutte, hvilken retning der skal bevæges i søgeområdet.Grådig tilgang:Bakkebestigningsalgoritmesøgning bevæger sig i den retning, som optimerer omkostningerne.Ingen tilbagesporing:Den sporer ikke søgerummet tilbage, da den ikke husker de tidligere tilstande.

State-space-diagram for bakkeklatring:

State-space-landskabet er en grafisk repræsentation af bakkeklatringsalgoritmen, som viser en graf mellem forskellige algoritmetilstande og målfunktion/omkostninger.

På Y-aksen har vi taget funktionen, som kan være en objektiv funktion eller omkostningsfunktion, og tilstandsrum på x-aksen. Hvis funktionen på Y-aksen er kostpris, er målet med søgning at finde det globale minimum og lokale minimum. Hvis Y-aksens funktion er Objektiv funktion, så er målet med søgningen at finde det globale maksimum og det lokale maksimum.

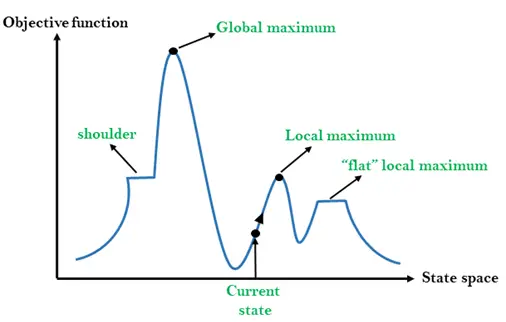
Forskellige regioner i det statslige rumlandskab:

Lokalt maksimum: Lokalt maksimum er en stat, der er bedre end dens nabostater, men der er også en anden stat, der er højere end den.

Globalt maksimum: Globalt maksimum er den bedst mulige tilstand af statens rumlandskab. Det har den højeste værdi af objektiv funktion.

Nuværende tilstand: Det er en tilstand i et landskabsdiagram, hvor en agent i øjeblikket er til stede.

Fladt lokalt maksimum: Det er et fladt rum i landskabet, hvor alle nuværende staters nabostater har samme værdi.

Skulder: Det er en plateau-region, som har en kant op ad bakke.

Typer af bakkeklatringsalgoritme:

• Enkel bakkeklatring:
• Stejleste-opstigning bakke-klatring:
• Stokastisk bakkeklatring:

1. Enkel bakkeklatring:

Simpel bakkeklatring er den enkleste måde at implementere en bakkeklatringsalgoritme på. Den evaluerer kun naboknudetilstanden ad gangen og vælger den første, der optimerer de nuværende omkostninger og indstiller den som en aktuel tilstand . Den kontrollerer kun, at den er en efterfølgertilstand, og hvis den finder bedre end den nuværende tilstand, så flyt ellers i samme tilstand. Denne algoritme har følgende funktioner:

• Mindre tidskrævende
• Mindre optimal løsning og løsningen er ikke garanteret

Algoritme for simpel bakkeklatring:

Trin 1:Evaluer starttilstanden, hvis det er måltilstand, så returner succes og stop.Trin 2:Sløjfe Indtil en løsning er fundet, eller der ikke er nogen ny operatør tilbage at søge.Trin 3:Vælg og anvend en operator til den aktuelle tilstand.Trin 4:Tjek ny tilstand:
1. Hvis det er måltilstand, så returner succes og stop.
2. Ellers, hvis den er bedre end den nuværende tilstand, så tildel ny tilstand som en nuværende tilstand.
3. Ellers, hvis ikke bedre end den nuværende tilstand, så vend tilbage til trin 2.
Trin 5:Afslut.

2. Stejleste stigning i bakkeklatring:

Den stejleste opstigningsalgoritme er en variation af simpel bakkeklatringsalgoritme. Denne algoritme undersøger alle naboknudepunkter i den aktuelle tilstand og vælger en naboknude, som er tættest på måltilstanden. Denne algoritme bruger mere tid, da den søger efter flere naboer

Algoritme for stejleste stigning i bakkeklatring:

Trin 1:Evaluer starttilstanden, hvis det er måltilstand, så returner succes og stop, ellers gør den nuværende tilstand som starttilstand.Trin 2:Loop indtil en løsning er fundet, eller den aktuelle tilstand ikke ændres.
1. Lad SUCC være en stat, så enhver efterfølger af den nuværende stat vil være bedre end den.
2. For hver operatør, der gælder for den aktuelle tilstand:
   1. Anvend den nye operator og generer en ny tilstand.
   2. Evaluer den nye tilstand.
   3. Hvis det er måltilstand, så returner det og afslut, ellers sammenligne det med SUCC.
   4. Hvis det er bedre end SUCC, så sæt ny tilstand som SUCC.
   5. Hvis SUCC er bedre end den aktuelle tilstand, skal du indstille den aktuelle tilstand til SUCC.
Trin 5:Afslut.

3. Stokastisk bakkeklatring:

Stokastisk bakkeklatring undersøger ikke for alle sine naboer, før de flytter. Denne søgealgoritme vælger snarere én naboknude tilfældigt og beslutter, om den skal vælges som en aktuel tilstand eller undersøge en anden tilstand.

Problemer i Hill Climbing Algorithm:

1. Lokalt maksimum: Et lokalt maksimum er en toptilstand i landskabet, som er bedre end hver af dens nabostater, men der er også en anden stat til stede, som er højere end det lokale maksimum.

Løsning: Backtracking teknik kan være en løsning af det lokale maksimum i statens rumlandskab. Opret en liste over den lovende sti, så algoritmen kan spore søgerummet tilbage og også udforske andre stier.

2. Plateau: Et plateau er det flade område af søgerummet, hvori alle nabotilstande i den aktuelle tilstand indeholder den samme værdi, fordi denne algoritme ikke finder nogen bedste retning at bevæge sig. En bakke-bestigningssøgning kan gå tabt i plateauområdet.

Løsning: Løsningen for plateauet er at tage store skridt eller meget små skridt, mens du søger, for at løse problemet. Vælg tilfældigt en tilstand, der er langt væk fra den aktuelle tilstand, så det er muligt, at algoritmen kan finde en ikke-plateauregion.

3. Kamme: En højderyg er en særlig form for det lokale maksimum. Det har et område, der er højere end dets omkringliggende områder, men selv har en hældning og kan ikke nås i et enkelt træk.

Løsning: Ved at bruge tovejssøgning eller ved at bevæge os i forskellige retninger kan vi forbedre dette problem.

Simuleret udglødning:

En bakkeklatringsalgoritme, der aldrig bevæger sig mod en lavere værdi, er garanteret ufuldstændig, fordi den kan sidde fast på et lokalt maksimum. Og hvis algoritmen anvender en tilfældig gåtur ved at flytte en efterfølger, kan den fuldføre, men ikke effektiv. Simuleret udglødning er en algoritme, som giver både effektivitet og fuldstændighed.

På mekanisk sigt Udglødning er en proces med at hærde et metal eller glas til en høj temperatur og derefter afkøle gradvist, så dette tillader metallet at nå en lavenergi-krystallinsk tilstand. Den samme proces bruges i simuleret annealing, hvor algoritmen vælger et tilfældigt træk i stedet for at vælge det bedste træk. Hvis den tilfældige bevægelse forbedrer tilstanden, følger den samme vej. Ellers følger algoritmen stien, som har en sandsynlighed på mindre end 1, eller den bevæger sig ned ad bakke og vælger en anden vej.