Den grådige metode er en af de strategier som Divide and conquer, der bruges til at løse problemerne. Denne metode bruges til at løse optimeringsproblemer. Et optimeringsproblem er et problem, der kræver enten maksimale eller minimale resultater. Lad os forstå gennem nogle udtryk.
Den grådige metode er den enkleste og ligetil tilgang. Det er ikke en algoritme, men det er en teknik. Hovedfunktionen af denne tilgang er, at beslutningen træffes på grundlag af de aktuelt tilgængelige oplysninger. Uanset hvad den aktuelle information er til stede, træffes beslutningen uden at bekymre sig om effekten af den aktuelle beslutning i fremtiden.
javascript søvn
Denne teknik bruges grundlæggende til at bestemme den mulige løsning, der måske eller måske ikke er optimal. Den mulige løsning er en delmængde, der opfylder de givne kriterier. Den optimale løsning er den løsning, som er den bedste og den mest fordelagtige løsning i undergruppen. I tilfælde af gennemførlig, hvis mere end én løsning opfylder de givne kriterier, vil disse løsninger blive betragtet som de mulige, mens den optimale løsning er den bedste løsning blandt alle løsningerne.
Karakteristika ved Greedy-metoden
Følgende er kendetegnene for en grådig metode:
- For at konstruere løsningen på en optimal måde, opretter denne algoritme to sæt, hvor et sæt indeholder alle de valgte elementer, og et andet sæt indeholder de afviste elementer.
- En Greedy-algoritme træffer gode lokale valg i håb om, at løsningen enten skal være gennemførlig eller optimal.
Komponenter af Greedy Algorithm
Komponenterne, der kan bruges i den grådige algoritme, er:
referencevariabel i java
Anvendelser af Greedy Algorithm
- Det bruges til at finde den korteste vej.
- Det bruges til at finde minimumspændingstræet ved hjælp af prim's algoritme eller Kruskal's algoritme.
- Det bruges i en jobrækkefølge med en deadline.
- Denne algoritme bruges også til at løse problemet med fraktioneret rygsæk.
Pseudokode for Greedy Algorithm
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Ovenstående er den grådige algoritme. I første omgang tildeles løsningen nulværdi. Vi passerer arrayet og antallet af elementer i den grådige algoritme. Inde i for-løkken vælger vi elementet et efter et og tjekker, om løsningen er gennemførlig eller ej. Hvis løsningen er gennemførlig, så udfører vi fagforeningen.
Lad os forstå gennem et eksempel.
Antag, at der er et problem 'P'. Jeg ønsker at rejse fra A til B vist som nedenfor:
P : A → B
Problemet er, at vi skal rejse denne rejse fra A til B. Der er forskellige løsninger til at gå fra A til B. Vi kan gå fra A til B pr. gang, bil, cykel, tog, flyvemaskine osv. Der er en begrænsning i rejsen, at vi skal rejse denne rejse inden for 12 timer. Hvis jeg kun tager tog eller fly, kan jeg tilbagelægge denne distance inden for 12 timer. Der er mange løsninger på dette problem, men der er kun to løsninger, der opfylder begrænsningen.
Hvis vi siger, at vi skal dække rejsen til minimumsomkostninger. Det betyder, at vi skal rejse denne afstand så minimum som muligt, så dette problem er kendt som et minimeringsproblem. Indtil nu har vi to mulige løsninger, nemlig en med tog og en anden med fly. Da rejser med tog vil føre til minimale omkostninger, så er det en optimal løsning. En optimal løsning er også den mulige løsning, men giver det bedste resultat, så løsningen er den optimale løsning med minimale omkostninger. Der ville kun være én optimal løsning.
Problemet, der kræver enten minimum eller maksimum resultat, så er dette problem kendt som et optimeringsproblem. Grådig metode er en af de strategier, der bruges til at løse optimeringsproblemerne.
python konstruktør
Ulemper ved at bruge Greedy algoritme
Grådig algoritme træffer beslutninger baseret på den information, der er tilgængelig i hver fase uden at overveje det bredere problem. Så der kan være en mulighed for, at den grådige løsning ikke giver den bedste løsning til ethvert problem.
Den følger det lokale optimale valg på hvert trin med det formål at finde det globale optimum. Lad os forstå gennem et eksempel.
Overvej grafen, som er givet nedenfor:
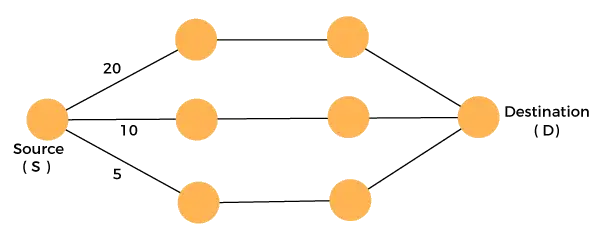
Vi skal rejse fra kilden til destinationen til minimale omkostninger. Da vi har tre mulige løsninger med omkostningsstier som 10, 20 og 5. 5 er minimumsomkostningsstien, så det er den optimale løsning. Dette er det lokale optimum, og på den måde finder vi det lokale optimum på hvert trin for at beregne den globale optimale løsning.
1 million i cifre
