Ford-Fulkerson-algoritmen er en meget brugt algoritme til at løse det maksimale flowproblem i et flownetværk. Det maksimale flow-problem involverer at bestemme den maksimale mængde flow, der kan sendes fra et kildepunkt til et synkepunkt i en rettet vægtet graf, underlagt kapacitetsbegrænsninger på kanterne.
Algoritmen fungerer ved iterativt at finde en forstærkende vej, som er en vej fra kilden til synken i restgrafen, dvs. grafen opnået ved at trække strømstrømmen fra kapaciteten af hver kant. Algoritmen øger derefter flowet langs denne vej med den maksimalt mulige mængde, som er minimumskapaciteten af kanterne langs stien.
Problem:
Givet en graf, der repræsenterer et flownetværk, hvor hver kant har en kapacitet. Også givet to hjørner kilde 's' og håndvask 't' i grafen, find det maksimalt mulige flow fra s til t med følgende begrænsninger:
- Flow på en kant overstiger ikke kantens givne kapacitet.
- Indgående flow er lig med udgående flow for hvert toppunkt undtagen s og t.
Overvej for eksempel følgende graf fra CLRS-bogen.
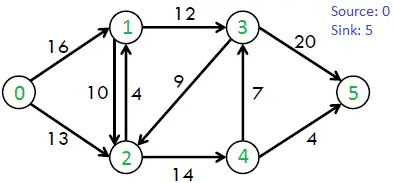
Det maksimalt mulige flow i ovenstående graf er 23.

Forudsætning: Max Flow Problem Introduktion
Ford-Fulkerson algoritme
Følgende er en simpel idé om Ford-Fulkerson-algoritmen:
- Start med indledende flow som 0.
- Mens der eksisterer en forstærkende vej fra kilden til vasken:
- Find en forstærkende sti ved hjælp af en hvilken som helst stifindende algoritme, såsom bredde-først-søgning eller dybde-først-søgning.
- Bestem mængden af flow, der kan sendes langs forstærkningsbanen, som er den minimale resterende kapacitet langs kanterne af banen.
- Forøg flowet langs forstærkningsbanen med den fastsatte mængde.
- Returner det maksimale flow.
Tidskompleksitet: Tidskompleksiteten af ovenstående algoritme er O(max_flow * E). Vi kører en løkke, mens der er en forstærkende sti. I værste fald kan vi tilføje 1 enhedsflow i hver iteration. Derfor bliver tidskompleksiteten O(max_flow * E).
Hvordan implementerer man ovenstående simple algoritme?
Lad os først definere begrebet Residual Graph, som er nødvendigt for at forstå implementeringen.
Restgraf af et flow-netværk er en graf, der angiver yderligere mulig flow. Hvis der er en vej fra kilde til synk i restgraf, så er det muligt at tilføje flow. Hver kant af en resterende graf har en værdi kaldet restkapacitet som er lig med den oprindelige kapacitet af kanten minus strømflow. Restkapacitet er som udgangspunkt kantens nuværende kapacitet.
Lad os nu tale om implementeringsdetaljer. Restkapaciteten er 0, hvis der ikke er nogen kant mellem to spidser af resterende graf. Vi kan initialisere restgrafen som original graf, da der ikke er noget indledende flow og initialt restkapacitet er lig med original kapacitet. For at finde en forøgelsessti kan vi enten lave en BFS eller DFS af restgrafen. Vi har brugt BFS i nedenstående implementering. Ved hjælp af BFS kan vi finde ud af, om der er en vej fra kilde til synk. BFS bygger også overordnet [] array. Ved at bruge parent[]-arrayet krydser vi den fundne sti og finder mulig strømning gennem denne sti ved at finde minimum restkapacitet langs stien. Vi tilføjer senere det fundne sti-flow til det samlede flow.
Det vigtige er, at vi skal opdatere resterende kapaciteter i restgrafen. Vi trækker sti-flow fra alle kanter langs stien, og vi tilføjer sti-flow langs de modsatte kanter. Vi er nødt til at tilføje sti-flow langs modsatte kanter, fordi det senere kan være nødvendigt at sende flow i modsat retning (se f.eks. følgende link).
Nedenfor er implementeringen af Ford-Fulkerson-algoritmen. For at gøre tingene enkle er grafen repræsenteret som en 2D-matrix.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Hvis vi finder en forbindelse til sink-noden, // så er der ingen mening i BFS længere. Vi // skal bare indstille dens overordnede og kan returnere // true if (v == t) { parent[ v] = u; returnere sandt; } q.push(v); forælder[v] = u; besøgt[v] = sand; } } } // Vi nåede ikke sink i BFS startende fra kilden, så // returnerer false return false; } // Returnerer det maksimale flow fra s til t i den givne graf int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Opret en restgraf og udfyld restgrafen // med givne kapaciteter i den originale graf som // restkapaciteter i residualgraf int rGraph[V] [V]; // Residual graf hvor rGraph[i][j] // angiver restkapacitet af kant // fra i til j (hvis der er en kant. Hvis // rGraph[i][j] er 0, så er der ikke) for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; int parent[V]; // Dette array er udfyldt af BFS og til // lagre sti int max_flow = 0; // Der er ingen flow initialt // Øg flowet, mens der er vej fra kilden til // sink while (bfs(rGraph, s, t, parent)) { // Find minimum restkapacitet af kanterne langs // stien udfyldt af BFS Eller vi kan sige find // maksimum flow gennem stien fundet int path_flow = INT_MAX for (v = t; v = s; parent[v]; path_flow = min(path_flow, rGraph[u][v] } // opdater restkapaciteten af kanterne og // omvendte kanter langs stien for (v = t; v != s; v = forælder[v]) { u = overordnet[v]; // Returner det overordnede flow retur max_flow; } // Driverprogram til at teste ovenstående funktioner int main() { // Lad os lave en graf vist i eksemplet ovenfor int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Hvis vi finder en forbindelse til sink // node, så er der ingen mening i BFS // længere. Vi skal bare indstille dens parent // og kan returnere true if (v == t) { parent[ v] = u; returnere sandt; } kø.add(v); forælder[v] = u; besøgt[v] = sand; } } } // Vi nåede ikke sink i BFS startende fra kilden, // så returner false return false; } // Returnerer det maksimale flow fra s til t i den givne // graf int fordFulkerson(int graf[][], int s, int t) { int u, v; // Lav en restgraf og udfyld den resterende // graf med givne kapaciteter i den originale graf // som restkapaciteter i restgraf // Residual graf hvor rGraph[i][j] angiver // restkapacitet af kant fra i til j (hvis der // er en kant. Hvis rGraph[i][j] er 0, så er der // ikke) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; // Dette array er udfyldt af BFS og for at gemme sti int parent[] = new int[ V]; int max_flow = 0; // Der er ikke noget flow til at begynde med af kanterne // langs stien udfyldt af BFS Eller vi kan sige // finde det maksimale flow gennem stien fundet int path_flow = Integer.MAX_VALUE for (v = t; v != s; v = parent[v ]) { u = parent[v]; path_flow = Math.min(path_flow, rGraph[u][v] } // opdater restkapaciteten af kanterne og // omvendte kanter langs stien for (v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow; flow max_flow += path_flow; } // Returner det overordnede flow return max_flow } // Driverprogram til at teste ovenstående funktioner public static void main(String[] args) kaster java.lang.Exception { // Lad os oprette en graf vist i ovenstående eksempel int graf[][] = ny int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = new MaxFlow(); System.out.println('Det maksimalt mulige flow er ' + m.fordFulkerson(graf, 0, 5)); } }> |
>
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
Javascript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Hvis vi finder en forbindelse til sink // node, så er der ingen mening i BFS // længere. Vi skal bare indstille dens parent // og kan returnere true if (v == t) { parent[ v] = u; returnere sandt; } kø.push(v); forælder[v] = u; besøgt[v] = sand; } } } // Vi nåede ikke sink i BFS startende // fra kilden, så returner false return false; } // Returnerer det maksimale flow fra s til t i // den givne graffunktion fordFulkerson(graf, s, t) { let u, v; // Opret en restgraf og udfyld // restgrafen med givne kapaciteter // i den originale graf som residual // kapaciteter i residualgraf // Residualgraf hvor rGraph[i][j] // angiver restkapacitet af kant / / fra i til j (hvis der er en kant. // Hvis rGraph[i][j] er 0, så er der // ikke) lad rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Denne matrix er udfyldt af BFS og for at gemme sti lad forælder = new Array(V // Der er ikke noget flow initialt lad max_flow = 0 // Augment the flow mens der // er sti fra source til sink while (bfs(rGraph, s, t); , parent)) { // Find minimum restkapacitet af kanterne // langs stien udfyldt af BFS. Eller vi kan sige // find det maksimale flow gennem stien, der er fundet ; v != s; v = parent[v]) { u = parent[v]; omvendte kanter langs stien for(v = t; v != s; v = forælder[v]) { u = forælder[v]; rGraph[v][u] + = path_flow; } // Tilføj path flow til det overordnede flow max_flow += path_flow } // Returner det overordnede flow return max_flow } // Driver-kode // Lad os oprette en graf vist i eksemplet ovenfor , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20], [0, 0, 0, 7, 0, 4], [0, 0, 0, 0, 0, 0]]; document.write('Det maksimalt mulige flow er ' + fordFulkerson(graf, 0, 5)); // Denne kode er bidraget af avanitrachhadiya2155> |
stak i ds
>
>Produktion
The maximum possible flow is 23>
Tidskompleksitet: O(|V| * E^2) ,hvor E er antallet af kanter og V er antallet af hjørner.
Rumkompleksitet :O(V) , da vi oprettede kø.
Ovenstående implementering af Ford Fulkerson Algorithm kaldes Edmonds-Karp algoritme . Ideen med Edmonds-Karp er at bruge BFS i Ford Fulkerson-implementering, da BFS altid vælger en vej med et minimum af kanter. Når BFS bruges, kan den værste tidskompleksitet reduceres til O(VE2). Ovenstående implementering bruger dog tilstødende matrixrepræsentation, hvor BFS tager O(V2) tid, er tidskompleksiteten af ovenstående implementering O(EV3) (Henvise CLRS bog for at bevise tidskompleksitet)
Dette er et vigtigt problem, da det opstår i mange praktiske situationer. Eksempler omfatter maksimering af transporten med givne trafikgrænser, maksimering af pakkeflow i computernetværk.
Dincs algoritme for Max-Flow.
Dyrke motion:
Rediger ovenstående implementering, så den kører i O(VE2) tid.
