FLOYD WARSHALL ALGORITHM - TECHCODEVIEW.COM

Det Floyd-Warshall algoritme , opkaldt efter dets skabere Robert Floyd og Stephen Warshall , er en grundlæggende algoritme inden for datalogi og grafteori. Det bruges til at finde de korteste veje mellem alle nodepar i en vægtet graf. Denne algoritme er yderst effektiv og kan håndtere grafer med begge positiv og n egative kantvægte , hvilket gør det til et alsidigt værktøj til at løse en lang række netværks- og forbindelsesproblemer.

Indholdsfortegnelse

Floyd Warshall algoritme
Idéen bag Floyd Warshall-algoritmen
Floyd Warshall Algoritme Algoritme
Pseudo-kode for Floyd Warshall Algorithm
Illustration af Floyd Warshall Algorithm
Kompleksitetsanalyse af Floyd Warshall-algoritmen
Hvorfor Floyd-Warshall Algorithm er bedre til tætte grafer og ikke for sparsomme grafer?
Vigtige interviewspørgsmål relateret til Floyd-Warshall
Virkelige applikationer af Floyd-Warshall Algorithm

Floyd-Warshall-Algorithm-banner

Floyd Warshall-algoritme:

Det Floyd Warshall algoritme er en alle par korteste vej algoritme i modsætning til Dijkstra og Bellman Ford som er single source korteste vej algoritmer. Denne algoritme virker for både instrueret og urettet vægtet grafer. Men det virker ikke for graferne med negative cyklusser (hvor summen af kanterne i en cyklus er negativ). Det følger Dynamisk programmering tilgang til at kontrollere alle mulige veje, der går gennem alle mulige knudepunkter, for at beregne den korteste afstand mellem hvert par knudepunkter.
hvordan fravælger du i gimp

Idéen bag Floyd Warshall-algoritmen:

Antag, at vi har en graf G[][] med I hjørner fra 1 til N . Nu skal vi evaluere en shortestPathMatrix[][] hvor s hortestPathMatrix[i][j] repræsenterer den korteste vej mellem toppunkter jeg og j .

Åbenbart den korteste vej imellem jeg til j vil have nogle k antal mellemknuder. Ideen bag floyd warshall-algoritmen er at behandle hvert eneste toppunkt fra 1 til N som en mellemknude én efter én.

Følgende figur viser ovenstående optimale understrukturegenskab i floyd warshall-algoritmen:

Floyd Warshall Algoritme Algoritme:

Initialiser løsningsmatrixen på samme måde som inputgrafmatricen som et første trin.
Opdater derefter løsningsmatrixen ved at betragte alle toppunkter som et mellemliggende toppunkt.
Ideen er at vælge alle toppunkter én efter én og opdatere alle korteste veje, som inkluderer det valgte toppunkt som et mellemliggende toppunkt i den korteste vej.
Når vi vælger toppunktnummer k som et mellemliggende toppunkt har vi allerede betragtet toppunkter {0, 1, 2, .. k-1} som mellemliggende hjørner.
For hvert par (i, j) af henholdsvis kilde- og destinationshjørnet er der to mulige tilfælde.
- k er ikke et mellemliggende toppunkt i korteste vej fra jeg til j . Vi beholder værdien af dist[i][j] Som det er.
- k er et mellemliggende toppunkt i korteste vej fra jeg til j . Vi opdaterer værdien af dist[i][j] som dist[i][k] + dist[k][j], hvis dist[i][j]> dist[i][k] + dist[k][j]

Pseudo-kode for Floyd Warshall Algorithm:`>`

For k = 0 til n – 1
For i = 0 til n – 1
For j = 0 til n – 1
Afstand[i, j] = min(Afstand[i, j], Afstand[i, k] + Afstand[k, j])

hvor i = kildeknude, j = destinationsknude, k = mellemknude

Illustration af Floyd Warshall Algorithm:

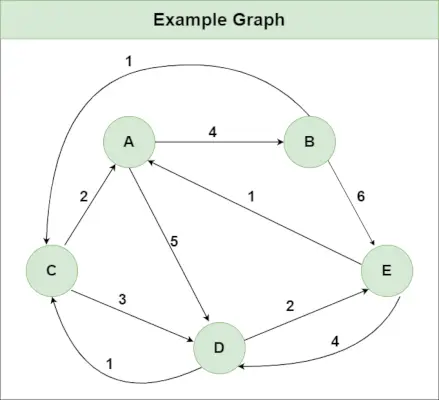
Antag, at vi har en graf som vist på billedet:

Trin 1 : Initialiser Afstand[][]-matricen ved hjælp af inputgrafen, således at Afstand[i][j]= vægt af kant fra jeg til j , også Afstand[i][j] = Uendelig, hvis der ikke er nogen kant fra jeg til j.

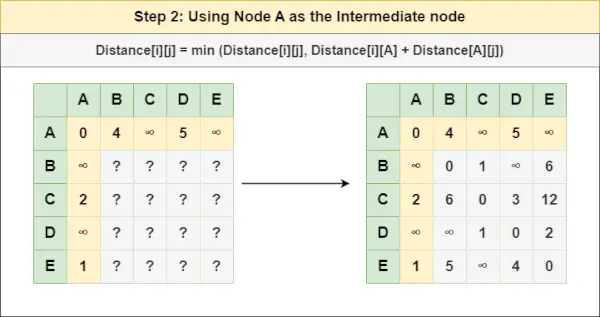
Trin 2 : Behandl node EN som en mellemknude og beregn Afstanden[][] for hvert {i,j} nodepar ved hjælp af formlen:
3d i autocad

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand fra i til EN ) + (Afstand fra EN til j))
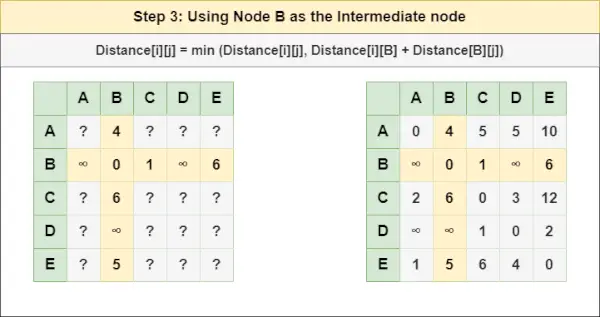
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ EN ] + Afstand[ EN ][j])

Trin 3 : Behandl node B som en mellemknude og beregn Afstanden[][] for hvert {i,j} nodepar ved hjælp af formlen:

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand fra i til B ) + (Afstand fra B til j))
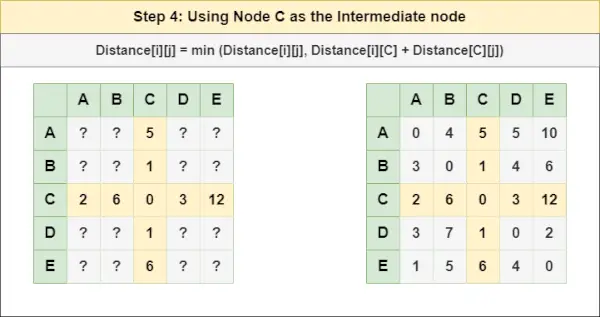
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ B ] + Afstand[ B ][j])

Trin 4 : Behandl node C som en mellemknude og beregn Afstanden[][] for hvert {i,j} nodepar ved hjælp af formlen:

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand fra i til C ) + (Afstand fra C til j))
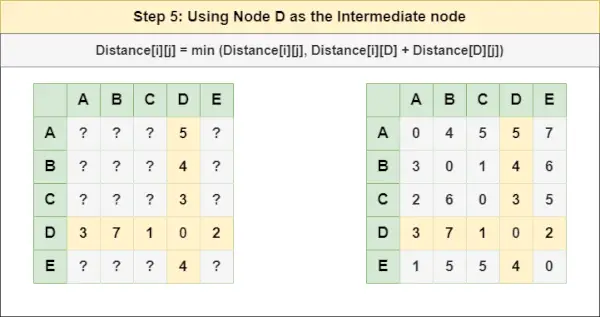
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ C ] + Afstand[ C ][j])

Trin 5 : Behandl node D som en mellemknude og beregn Afstanden[][] for hvert {i,j} nodepar ved hjælp af formlen:
konverter char til streng

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand fra i til D ) + (Afstand fra D til j))
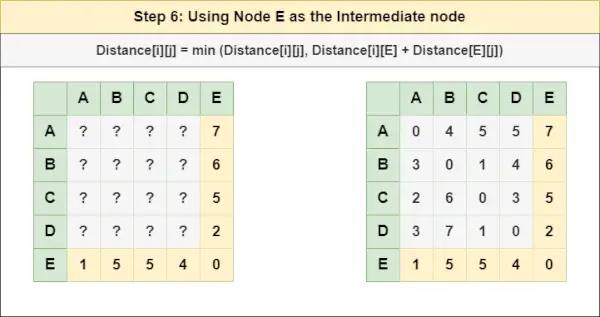
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ D ] + Afstand[ D ][j])

Trin 6 : Behandl node OG som en mellemknude og beregn Afstanden[][] for hvert {i,j} nodepar ved hjælp af formlen:
er lig med streng i java

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand fra i til OG ) + (Afstand fra OG til j))
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ OG ] + Afstand[ OG ][j])

Trin 7 : Da alle noderne er blevet behandlet som en mellemknude, kan vi nu returnere den opdaterede Distance[][] matrix som vores svarmatrix.

Anbefalet praksis Prøv det!

Nedenfor er implementeringen af ovenstående tilgang:

C++

 // C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Før start af en iteration har vi korteste afstande mellem alle par af toppunkter, således at de korteste afstande kun betragter toppunkterne i sæt {0, 1, 2, .. k-1} som mellemliggende toppunkter.  ----> Efter afslutningen af en iteration, vertex no. k tilføjes til sættet af mellemliggende hjørner, og mængden bliver {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Udskriv den korteste afstand matrix printSolution(dist); } /* En hjælpefunktion til at udskrive løsning */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graf[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Funktionskald floydWarshall(graf);  retur 0; } // Denne kode er bidraget af Mythri J L>

 // C Program for Floyd Warshall Algorithm #include  // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough  value. This value will be used  for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Før start af en iteration har vi korteste afstande mellem alle par af toppunkter, således at de korteste afstande kun betragter toppunkterne i sæt {0, 1, 2, .. k-1} som mellemliggende toppunkter.  ----> Efter afslutningen af en iteration, vertex no. k tilføjes til sættet af mellemliggende hjørner, og mængden bliver {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j])  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) {  printf(  'The following matrix shows the shortest distances'  ' between every pair of vertices 
');  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  printf('%7s', 'INF');  else  printf('%7d', dist[i][j]);  }  printf('
');  } } // driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graf[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Funktionskald floydWarshall(graf);  retur 0; }>

Java

 // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Før start af en iteration har vi korteste afstande mellem alle par af toppunkter, således at de korteste afstande kun betragter toppunkterne i sæt {0, 1, 2, .. k-1} som mellemliggende toppunkter.  ----> Efter afslutningen af en iteration, vertex no. k tilføjes til sættet af mellemliggende hjørner, og mængden bliver {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graf[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Funktionskald a.floydWarshall(graf);  } } // Bidraget af Aakash Hasija>

Python3

 # Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Før start af en iteration har vi korteste afstande mellem alle par af toppunkter, således at de korteste afstande kun betragter toppunkterne i mængden {0, 1, 2, .. k-1} som mellemliggende toppunkter.  ----> Efter afslutningen af en iteration, vertex no. k tilføjes til sættet af mellemliggende hjørner, og mængden bliver {0, 1, 2, .. k} ''' for k i område(V): # vælg alle knudepunkter som kilde en efter en for i i interval(V): # Vælg alle toppunkter som destination for # ovenfor valgte kilde for j i interval(V): # Hvis toppunktet k er på den korteste vej fra # i til j, skal du opdatere værdien af dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # En hjælpefunktion til at udskrive løsningen def printSolution (dist): print('Følgende matrix viser de korteste afstande mellem hvert par af hjørner') for i i området(V): for j i området(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Driverkode if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' graf = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Funktionskald floydWarshall(graph) # Denne kode er bidraget af Mythri J L>

 // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Før start af en iteration har vi korteste afstande mellem alle par af toppunkter, således at de korteste afstande kun betragter toppunkterne i sæt {0, 1, 2, .. k-1} som mellemliggende toppunkter.  ---> Efter afslutningen af en iteration, vertex no. k tilføjes til sættet af mellemliggende hjørner, og mængden bliver {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] graf = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Funktionskald a.floydWarshall(graf);  } } // Denne artikel er bidraget af // Abdul Mateen Mohammed>

Javascript

 // A JavaScript program for Floyd Warshall All  // Pairs Shortest Path algorithm.  var INF = 99999;  class AllPairShortestPath {  constructor() {  this.V = 4;  }  floydWarshall(graph) {  var dist = Array.from(Array(this.V), () =>new Array(this.V).fill(0));  var i, j, k;  // Initialiser løsningsmatrixen // samme som inputgrafmatricen // Eller vi kan sige de indledende //-værdier for korteste afstande // er baseret på korteste veje // i betragtning af ingen mellemliggende // toppunkt for (i = 0; i< this.V; i++) {  for (j = 0; j < this.V; j++) {  dist[i][j] = graph[i][j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Før start af en iteration har vi korteste afstande mellem alle par af toppunkter, således at de korteste afstande kun betragter toppunkterne i sæt {0, 1, 2, .. k-1} som mellemliggende toppunkter.  ---> Efter afslutningen af en iteration, vertex no. k tilføjes til sættet af mellemliggende hjørner, og mængden bliver {0, 1, 2, .. k} */ for (k = 0; k< this.V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < this.V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < this.V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j]) {  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  }  // Print the shortest distance matrix  this.printSolution(dist);  }  printSolution(dist) {  document.write(  'Following matrix shows the shortest ' +  'distances between every pair of vertices '  );  for (var i = 0; i < this.V; ++i) {  for (var j = 0; j < this.V; ++j) {  if (dist[i][j] == INF) {  document.write(' INF ');  } else {  document.write('  ' + dist[i][j] + ' ');  }  }  document.write(' ');  }  }  }  // Driver Code  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var graf = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = new AllPairShortestPath();  // Udskriv løsningen a.floydWarshall(graf);    // Denne kode er bidraget af rdtaank.>

PHP

  // PHP Program for Floyd Warshall Algorithm  // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm  function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix   that will finally have the shortest   distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same   as input graph matrix. Or we can say the   initial values of shortest distances are   based on shortest paths considering no   intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set   of intermediate vertices.   --->Før start af en iteration har vi korteste afstande mellem alle par af toppunkter, således at de korteste afstande kun betragter toppunkterne i sæt {0, 1, 2, .. k-1} som mellemliggende toppunkter.   ----> Efter afslutningen af en iteration, vertex no. k tilføjes til sættet af mellemliggende hjørner, og mængden bliver {0, 1, 2, .. k} */ for ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one  for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination  // for the above picked source  for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from  // i to j, then update the value of dist[i][j]  if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix  printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices 
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph  $V = 4 ; /* Define Infinite as a large enough  value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph   10  (0)------->(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $graf = array(array(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), array($INF, $INF, $INF, 0)); // Funktionskald floydWarshall($graf, $V, $INF); // Denne kode er bidraget af Ryuga ?>>

Produktion

The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Kompleksitetsanalyse af Floyd Warshall-algoritmen:

Tidskompleksitet: O(V³), hvor V er antallet af hjørner i grafen, og vi kører tre indlejrede løkker hver af størrelse V
Hjælpeplads: O(V²), for at skabe en 2-D matrix for at gemme den korteste afstand for hvert par knudepunkter.

Bemærk : Ovenstående program udskriver kun de korteste afstande. Vi kan modificere løsningen til at printe de korteste veje også ved at gemme forgængerinformationen i en separat 2D-matrix.

Hvorfor Floyd-Warshall Algorithm er bedre til tætte grafer og ikke for sparsomme grafer?

Tæt graf : En graf, hvor antallet af kanter er væsentligt meget højere end antallet af hjørner.
Sparsom graf : En graf, hvor antallet af kanter er meget lavt.

Uanset hvor mange kanter der er i grafen Floyd Warshall algoritme kører for O(V³) gange derfor er den bedst egnet til Tætte grafer . I tilfælde af sparsomme grafer, Johnsons algoritme er mere egnet.

Hvordan opdager man negativ cyklus i en graf ved hjælp af Floyd Warshall-algoritmen?
Hvordan er Floyd-warshall-algoritmen forskellig fra Dijkstras algoritme?
Hvordan er Floyd-warshall-algoritmen forskellig fra Bellman-Ford-algoritmen?

Virkelige applikationer af Floyd-Warshall-algoritmen:

I computernetværk kan algoritmen bruges til at finde den korteste vej mellem alle par af noder i et netværk. Dette betegnes som netværk routing .
Flight Connectivity I luftfartsindustrien for at finde den korteste vej mellem lufthavnene.
GIS ( Geografiske informationssystemer ) applikationer involverer ofte analyse af geografiske data, såsom vejnet, for at finde de korteste veje mellem lokationer.
Kleenes algoritme som er en generalisering af floyd warshall, kan bruges til at finde regulære udtryk for et regulært sprog.