• Finite state-maskine bruges til at genkende mønstre.
• Finite automata-maskine tager symbolstrengen som input og ændrer dens tilstand i overensstemmelse hermed. I inputtet, når et ønsket symbol er fundet, sker overgangen.
• Under overgangen kan automaten enten flytte til den næste tilstand eller forblive i den samme tilstand.
• FA har to tilstande: acceptere tilstand eller afvise tilstand. Når inputstrengen er behandlet med succes, og automaten har nået sin endelige tilstand, vil den acceptere.

En endelig automat består af følgende:

Q: endeligt sæt af tilstande
∑: begrænset sæt af inputsymbol
q0: begyndelsestilstand
F: sluttilstand
d: Overgangsfunktion

Overgangsfunktion kan defineres som

 δ: Q x ∑ →Q 

FA karakteriseres på to måder:

1. DFA (finite automata)
2. NDFA (non-deterministic finite automata)

DFA

DFA står for Deterministic Finite Automata. Deterministisk refererer til det unikke ved beregningen. I DFA går inputtegnet kun til én tilstand. DFA accepterer ikke nul-bevægelsen, hvilket betyder, at DFA ikke kan ændre tilstand uden noget inputtegn.

DFA har fem tuples {Q, ∑, q0, F, δ}

Eksempel

Se et eksempel på deterministiske endelige automater:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}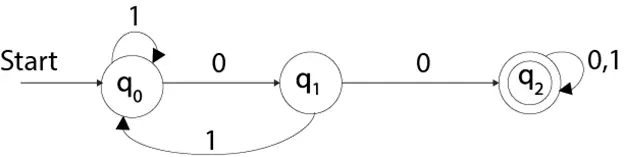 

NDFA

NDFA henviser til Non Deterministic Finite Automata. Det bruges til at overføre et vilkårligt antal tilstande for et bestemt input. NDFA accepterer NULL-bevægelsen, hvilket betyder, at den kan ændre tilstand uden at læse symbolerne.

NDFA har også fem stater som DFA. Men NDFA har en anden overgangsfunktion.

Overgangsfunktion af NDFA kan defineres som:

Eksempel

Se et eksempel på ikke-deterministiske endelige automater:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}