Udtrykstræet er et træ, der bruges til at repræsentere de forskellige udtryk. Trædatastrukturen bruges til at repræsentere udtryksudsagn. I dette træ betegner den interne node altid operatørerne.
- Bladknuderne angiver altid operanderne.
- Operationerne udføres altid på disse operander.
- Operatøren, der er til stede i træets dybde, har altid højeste prioritet.
- Operatøren, som ikke er meget i dybden i træet, har altid den laveste prioritet i forhold til de operatører, der ligger i dybden.
- Operanden vil altid være til stede i en dybde af træet; derfor betragtes det som højeste prioritet blandt alle operatører.
- Kort sagt kan vi opsummere det som, at værdien i en dybde af træet har højeste prioritet sammenlignet med de andre operatører, der er til stede i toppen af træet.
- Hovedanvendelsen af disse udtrykstræer er, at den er vant til vurdere, analysere og modificere de forskellige udtryk.
- Det bruges også til at finde ud af associativiteten af hver operator i udtrykket.
- For eksempel er + operatoren den venstre-associative og / er den højre-associative.
- Dilemmaet ved denne associativitet er blevet ryddet op ved at bruge udtrykket træer.
- Disse udtrykstræer er dannet ved at bruge en kontekstfri grammatik.
- Vi har knyttet en regel i kontekstfri grammatik foran hver grammatikproduktion.
- Disse regler er også kendt som semantiske regler, og ved at bruge disse semantiske regler kan vi let være i stand til at konstruere udtrykstræerne.
- Det er en af de vigtigste dele af compilerdesign og hører til den semantiske analysefase.
- I denne semantiske analyse vil vi bruge de syntaks-rettede oversættelser, og i form af output vil vi producere det kommenterede parsetræ.
- Et kommenteret parsetræ er intet andet end den simple parse, der er knyttet til typeattributten og hver produktionsregel.
- Hovedformålet med at bruge udtrykstræerne er at lave komplekse udtryk og kan nemt evalueres ved hjælp af disse udtrykstræer.
- Det er uforanderligt, og når vi først har oprettet et udtrykstræ, kan vi ikke ændre det eller modificere det yderligere.
- For at foretage flere ændringer er det nødvendigt at konstruere det nye udtrykstræ helt.
- Det bruges også til at løse evalueringen af postfix-, præfiks- og infix-udtryk.
Udtrykstræer spiller en meget vigtig rolle i at repræsentere sprogniveau kode i form af dataene, som hovedsageligt er lagret i den trælignende struktur. Det bruges også i hukommelsesrepræsentationen af lambda udtryk. Ved at bruge trædatastrukturen kan vi udtrykke lambda-udtrykket mere transparent og eksplicit. Det oprettes først for at konvertere kodesegmentet til datasegmentet, så udtrykket nemt kan evalueres.
Udtrykstræet er et binært træ, hvor hver ekstern knude eller bladknude svarer til operanden, og hver intern eller overordnet knude svarer til operatorerne, så for eksempel ville udtrykstræ for 7 + ((1+8)*3) være:
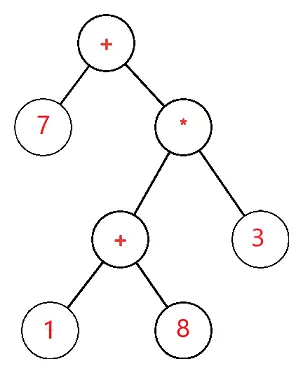
Lad S være udtrykstræet
Hvis S ikke er nul, så
Hvis S.value er en operand, så
Returner S.værdi
x = solve(S.venstre)
y = solve(S.right)
Returner beregne(x, y, S.værdi)
Her i ovenstående eksempel brugte udtrykstræet kontekstfri grammatik.
Vi har nogle produktioner forbundet med nogle produktionsregler i denne grammatik, hovedsagelig kendt som semantiske regler . Vi kan definere den resultatproducerende ud fra de tilsvarende produktionsregler ved hjælp af disse semantiske regler. Her har vi brugt værdiparameteren, som vil beregne resultatet og returnere det til grammatikkens startsymbol. S.left vil beregne det venstre underordnede af noden, og på samme måde kan det højre underordnede af knudepunktet beregnes ved hjælp af S.right parameteren.
Brug af udtrykstræ
- Hovedformålet med at bruge udtrykstræerne er at lave komplekse udtryk og kan nemt evalueres ved hjælp af disse udtrykstræer.
- Det bruges også til at finde ud af associativiteten af hver operator i udtrykket.
- Det bruges også til at løse evalueringen af postfix-, præfiks- og infix-udtryk.
Implementering af et udtrykstræ
For at implementere udtrykstræet og skrive dets program, skal vi bruge en stak datastruktur.
Da vi ved, at stakken er baseret på sidst ind først ud LIFO-princippet, er dataelementet, der for nylig blev skubbet ind i stakken, blevet poppet ud, når det var nødvendigt. Til dens implementering bruges de to vigtigste operationer af stakken, push og pop. Ved at bruge push-operationen vil vi skubbe dataelementet ind i stakken, og ved at bruge pop-operationen vil vi fjerne dataelementet fra stakken.
Hovedfunktioner af stakken i implementeringen af udtrykstræet:
Først og fremmest vil vi scanne det givne udtryk til venstre mod højre måde, derefter en efter en kontrollere det identificerede tegn,
- Hvis et scannet tegn er en operand, anvender vi push-operationen og skubber den ind i stakken.
- Hvis et scannet tegn er en operator, vil vi anvende pop-operationen i det for at fjerne de to værdier fra stakken for at gøre dem til dets underordnede, og derefter vil vi skubbe den nuværende overordnede node tilbage i stakken.
Implementering af udtrykstræ i C programmeringssprog
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Outputtet af ovenstående program er:
X + Y * Z / W
Implementering af Expression tree i C++ programmeringssprog
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Outputtet af ovenstående program er:
X + Y * Z / W
Implementering af udtrykstræ i Java programmeringssprog
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 