Eksempel 1:
Design en NFA til overgangstabellen som angivet nedenfor:
| Nuværende tilstand | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | e |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Løsning:
Overgangsdiagrammet kan tegnes ved at bruge kortlægningsfunktionen som angivet i tabellen.
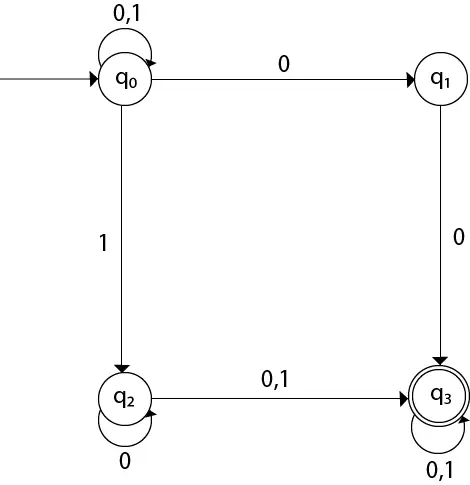
Her,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Eksempel 2:
Design en NFA med ∑ = {0, 1} accepterer alle strenge, der ender med 01.
Løsning:

Derfor ville NFA være:

Eksempel 3:
Design en NFA med ∑ = {0, 1}, hvor dobbelt '1' efterfølges af dobbelt '0'.
Løsning:
FA med dobbelt 1 er som følger:

Det skal umiddelbart efterfølges af dobbelt 0.
Derefter,
java hvis andet

Nu før dobbelt 1 kan der være en hvilken som helst streng på 0 og 1. På samme måde kan der efter dobbelt 0 være en hvilken som helst streng på 0 og 1.
Derfor bliver NFA:

Overvejer nu strengen 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Eksempel 4:
Design en NFA, hvor hele strengen indeholder en understreng 1110.
Løsning:
Sproget består af hele strengen, der indeholder understreng 1010. Det delvise overgangsdiagram kan være:

Nu som 1010 kunne være understrengen. Derfor vil vi tilføje input 0'erne og 1'erne, så understrengen 1010 af sproget kan opretholdes. Derfor bliver NFA:

Overgangstabel for ovenstående overgangsdiagram kan gives nedenfor:
| Nuværende tilstand | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Overvej en streng 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Sidder fast! Da der ikke er nogen sti fra q2 for inputsymbol 0. Vi kan behandle streng 111010 på en anden måde.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Som tilstand er q5 accepttilstanden. Vi får hele det scannede, og vi nåede til den endelige tilstand.
Eksempel 5:
Design en NFA med ∑ = {0, 1} accepterer alle strenge, hvor det tredje symbol fra højre ende altid er 0.
Løsning:

Således får vi det tredje symbol fra højre ende som '0' altid. NFA kan være:
indtastning af streng i java

Ovenstående billede er en NFA, fordi i tilstand q0 med input 0, kan vi enten gå til tilstand q0 eller q1.
