Eulerian sti er en sti i en graf, der besøger hver kant nøjagtigt én gang. Eulerian Circuit er en Eulersk sti, der starter og slutter på samme toppunkt.
css overgangsopacitet


Hvordan finder man ud af, om en given graf er Eulersk eller ej?
Problemet er det samme som det følgende spørgsmål. Er det muligt at tegne en given graf uden at løfte blyanten fra papiret og uden at spore nogen af kanterne mere end én gang.
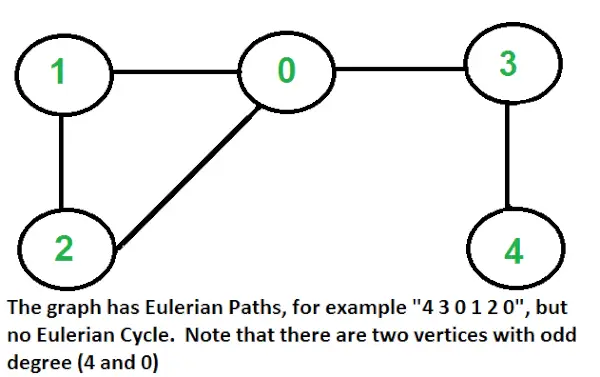
En graf kaldes Eulersk, hvis den har en Eulersk cyklus og kaldes semi-eulerisk, hvis den har en Eulersk sti. Problemet ligner Hamiltonian Path, som er NP komplet problem for en generel graf. Heldigvis kan vi finde ud af, om en given graf har en Eulerian Path eller ej i polynomisk tid. Faktisk kan vi finde det i O(V+E) tid.
Følgende er nogle interessante egenskaber ved urettede grafer med en Eulersk sti og cyklus. Vi kan bruge disse egenskaber til at finde ud af, om en graf er Eulersk eller ej.
Eulersk cyklus: En urettet graf har Eulersk cyklus, hvis følgende to betingelser er sande.
- Alle hjørner med ikke-nul grader er forbundet. Vi er ligeglade med hjørner med nul grader, fordi de ikke tilhører Eulerian Cycle eller Path (vi betragter kun alle kanter).
- Alle hjørner har lige grad.
Eulerian sti: En urettet graf har Eulerian Path, hvis følgende to betingelser er sande.
- Samme som betingelse (a) for Eulersk cyklus.
- Hvis nul eller to hjørner har ulige grad, og alle andre hjørner har lige grad. Bemærk, at kun et toppunkt med ulige grad ikke er muligt i en urettet graf (summen af alle grader er altid lige i en urettet graf)
Bemærk, at en graf uden kanter betragtes som Eulerian, fordi der ikke er nogen kanter at krydse.
Hvordan virker det?
I Eulersk sti går vi, hver gang vi besøger et toppunkt v, gennem to ubesøgte kanter med det ene endepunkt som v. Derfor skal alle midterpunkter i Eulersk sti have lige grad. For Eulersk cyklus kan ethvert toppunkt være midterpunkt, derfor skal alle toppunkter have lige grad.
Implementering:
C++
// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> >int> V;>// No. of vertices> >list<>int>>*adj;>// A dynamic array of adjacency lists> public>:> >// Constructor and destructor> >Graph(>int> V) {>this>->V = V; adj =>new> list<>int>>[I]; }> >~Graph() {>delete> [] adj; }>// To avoid memory leak> >// function to add an edge to graph> >void> addEdge(>int> v,>int> w);> >// Method to check if this graph is Eulerian or not> >int> isEulerian();> >// Method to check if all non-zero degree vertices are connected> >bool> isConnected();> >// Function to do DFS starting from v. Used in isConnected();> >void> DFSUtil(>int> v,>bool> visited[]);> };> void> Graph::addEdge(>int> v,>int> w)> {> >adj[v].push_back(w);> >adj[w].push_back(v);>// Note: the graph is undirected> }> void> Graph::DFSUtil(>int> v,>bool> visited[])> {> >// Mark the current node as visited and print it> >visited[v] =>true>;> >// Recur for all the vertices adjacent to this vertex> >list<>int>>::iterator i;> >for> (i = adj[v].begin(); i != adj[v].end(); ++i)> >if> (!visited[*i])> >DFSUtil(*i, visited);> }> // Method to check if all non-zero degree vertices are connected.> // It mainly does DFS traversal starting from> bool> Graph::isConnected()> {> >// Mark all the vertices as not visited> >bool> visited[V];> >int> i;> >for> (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) returnere falsk; returnere sandt; } /* Funktionen returnerer en af følgende værdier 0 --> Hvis grafen ikke er Eulersk 1 --> Hvis grafen har en Euler-sti (semi-eulerisk) 2 --> Hvis grafen har en Euler-kredsløb (Eulerian) */ int Graph::isEulerian() { // Tjek om alle ikke-nul graders hjørner er forbundet, hvis (isConnected() == falsk) returnerer 0; // Tæl toppunkter med ulige grad int ulige = 0; for (int i = 0; i if (adj[i].size() & 1) ulige++; // Hvis antallet er mere end 2, er grafen ikke Eulerian if (ulige> 2) returnerer 0; // Hvis ulige count er 2, så semi-eulerian // Hvis ulige antal er 0, så eulerian // Bemærk at ulige count aldrig kan være 1 for urettet graf returnerer (ulige) } // Funktion til at køre testcases test(Graph &g) { int res = g.isEulerian( if (res == 0) cout<< 'graph is not Eulerian
'; else if (res == 1) cout << 'graph has a Euler path
'; else cout << 'graph has a Euler cycle
'; } // Driver program to test above function int main() { // Let us create and test graphs shown in above figures Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); test(g1); Graph g2(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); test(g2); Graph g3(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); test(g3); // Let us create a graph with 3 vertices // connected in the form of cycle Graph g4(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); test(g4); // Let us create a graph with all vertices // with zero degree Graph g5(3); test(g5); return 0; }> |
lort
>
>
Java
// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> >private> int> V;>// No. of vertices> >// Array of lists for Adjacency List Representation> >private> LinkedList adj[];> >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> LinkedList[v];> >for> (>int> i=>0>; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) returnere falsk; returnere sandt; } /* Funktionen returnerer en af følgende værdier 0 --> Hvis grafen ikke er Eulersk 1 --> Hvis grafen har en Euler-sti (semi-eulerisk) 2 --> Hvis grafen har en Euler-kredsløb (Eulerian) */ int isEulerian() { // Tjek, om alle ikke-nul graders hjørner er forbundet, hvis (isConnected() == falsk) returnerer 0; // Tæl toppunkter med ulige grad int ulige = 0; for (int i = 0; i if (adj[i].size()%2!=0) ulige++; // Hvis antallet er mere end 2, så er grafen ikke Eulerian if (ulige> 2) returnerer 0; / / Hvis ulige tæller er 2, så semi-eulerian er 0, så eulerian // Bemærk at ulige count aldrig kan være 1 for urettet graf returnerer (ulige==2)? Funktion til at køre testcases void test() { int res = isEulerian(); out.println('graf har en Euler-sti'); else System.out.println('graf har en Euler-cyklus' } // Driver-metode public static void main(String args[]) { / / Lad os oprette og teste grafer vist i ovenstående figurer. Graph g1.addEdge(1, 0), g1.addEdge(2; (0, 3); g1.addEdge(3, 4); addEdge(2, 1, g2.addEdge(3, 4, 0) Graph(5); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Lad os lave en graf med 3 toppunkter // forbundet i form af cyklus Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Lad os lave en graf med alle hjørner // med nul grader Graph g5 = new Graph(3); g5.test(); } } // Denne kode er bidraget af Aakash Hasija> |
>
>
Python3
numpy meshgrid
# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections>import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> >def> __init__(>self>, vertices):> >self>.V>=> vertices># No. of vertices> >self>.graph>=> defaultdict(>list>)># default dictionary to store graph> ># function to add an edge to graph> >def> addEdge(>self>, u, v):> >self>.graph[u].append(v)> >self>.graph[v].append(u)> ># A function used by isConnected> >def> DFSUtil(>self>, v, visited):> ># Mark the current node as visited> >visited[v]>=> True> ># Recur for all the vertices adjacent to this vertex> >for> i>in> self>.graph[v]:> >if> visited[i]>=>=> False>:> >self>.DFSUtil(i, visited)> >'''Method to check if all non-zero degree vertices are> >connected. It mainly does DFS traversal starting from> >node with non-zero degree'''> >def> isConnected(>self>):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.V)> ># Find a vertex with non-zero degree> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i]) !>=> 0>:> >break> ># If there are no edges in the graph, return true> >if> i>=>=> self>.V>->1>:> >return> True> ># Start DFS traversal from a vertex with non-zero degree> >self>.DFSUtil(i, visited)> ># Check if all non-zero degree vertices are visited> >for> i>in> range>(>self>.V):> >if> visited[i]>=>=> False> and> len>(>self>.graph[i])>>0>:> >return> False> >return> True> >'''The function returns one of the following values> >0 -->Hvis grafen ikke er Eulerian> >1 -->Hvis grafen har en Euler-sti (semi-eulerisk)> >2 -->Hvis grafen har et Euler-kredsløb (Eulerian) '''> >def> isEulerian(>self>):> ># Check if all non-zero degree vertices are connected> >if> self>.isConnected()>=>=> False>:> >return> 0> >else>:> ># Count vertices with odd degree> >odd>=> 0> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i])>%> 2> !>=> 0>:> >odd>+>=> 1> >'''If odd count is 2, then semi-eulerian.> >If odd count is 0, then eulerian> >If count is more than 2, then graph is not Eulerian> >Note that odd count can never be 1 for undirected graph'''> >if> odd>=>=> 0>:> >return> 2> >elif> odd>=>=> 2>:> >return> 1> >elif> odd>>2>:> >return> 0> ># Function to run test cases> >def> test(>self>):> >res>=> self>.isEulerian()> >if> res>=>=> 0>:> >print>(>'graph is not Eulerian'>)> >elif> res>=>=> 1>:> >print>(>'graph has a Euler path'>)> >else>:> >print>(>'graph has a Euler cycle'>)> # Let us create and test graphs shown in above figures> g1>=> Graph(>5>)> g1.addEdge(>1>,>0>)> g1.addEdge(>0>,>2>)> g1.addEdge(>2>,>1>)> g1.addEdge(>0>,>3>)> g1.addEdge(>3>,>4>)> g1.test()> g2>=> Graph(>5>)> g2.addEdge(>1>,>0>)> g2.addEdge(>0>,>2>)> g2.addEdge(>2>,>1>)> g2.addEdge(>0>,>3>)> g2.addEdge(>3>,>4>)> g2.addEdge(>4>,>0>)> g2.test()> g3>=> Graph(>5>)> g3.addEdge(>1>,>0>)> g3.addEdge(>0>,>2>)> g3.addEdge(>2>,>1>)> g3.addEdge(>0>,>3>)> g3.addEdge(>3>,>4>)> g3.addEdge(>1>,>3>)> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4>=> Graph(>3>)> g4.addEdge(>0>,>1>)> g4.addEdge(>1>,>2>)> g4.addEdge(>2>,>0>)> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5>=> Graph(>3>)> g5.test()> # This code is contributed by Neelam Yadav> |
>
>
C#
// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> >private> int> V;>// No. of vertices> > >// Array of lists for Adjacency List Representation> >private> List<>int>>[]adj;> > >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> List<>int>>[i];> >for> (>int> i=0; i adj[i] = new List |
>
>
Javascript
kan en abstrakt klasse have en konstruktør
> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> >// Constructor> >constructor(v)> >{> >this>.V = v;> >this>.adj =>new> Array(v);> >for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i |
>
>Produktion
graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle>
Tidskompleksitet: O(V+E)
Rumkompleksitet: O(V+E)
Næste artikler:
Eulersk sti og kredsløb for en rettet grafer.
Fleurys algoritme til at udskrive en Eulersk sti eller kredsløb?
