Divide and Conquer er et algoritmisk mønster. I algoritmiske metoder er designet at tage en tvist om et kæmpe input, dele input i mindre stykker, afgøre problemet på hver af de små stykker og derefter flette de stykvise løsninger sammen til en global løsning. Denne mekanisme til at løse problemet kaldes Divide & Conquer-strategien.

Divide and Conquer-algoritmen består af en tvist ved hjælp af de følgende tre trin.

Deledet oprindelige problem til et sæt underproblemer.Erobre:Løs hvert delproblem individuelt, rekursivt.Forene:Sammensæt løsningerne af delproblemerne for at få løsningen på hele problemet.

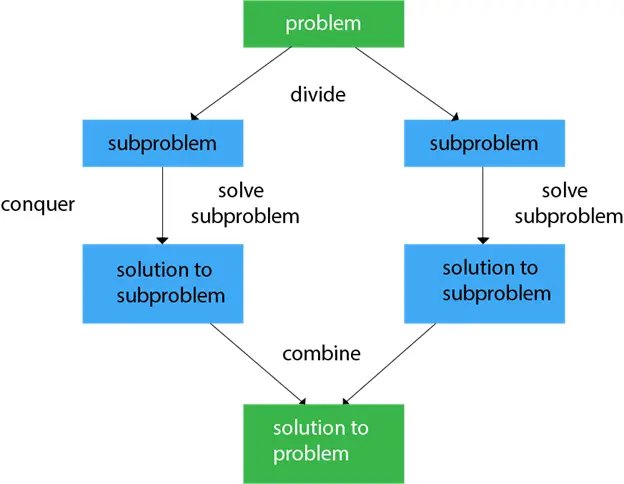
Generelt kan vi følge del-og-hersk tilgang i en tre-trins proces.

Eksempler: De specifikke computeralgoritmer er baseret på Divide & Conquer-tilgangen:

1. Maksimum og minimum problem
2. Binær søgning
3. Sortering (flet sortering, hurtig sortering)
4. Hanois tårn.

Fundamental of Divide & Conquer-strategi:

Der er to grundlæggende i Divide & Conquer-strategien:

1. Relationsformel
2. Standsningstilstand

1. Relationsformel: Det er formlen, som vi genererer ud fra den givne teknik. Efter generering af Formel anvender vi D&C Strategy, dvs. vi bryder problemet rekursivt og løser de ødelagte delproblemer.

2. Standsningstilstand: Når vi bryder problemet ved hjælp af Divide & Conquer Strategy, så skal vi vide, hvor lang tid, vi skal anvende divide & conquer. Så tilstanden, hvor behovet for at stoppe vores rekursionstrin af D&C, kaldes som Stopningstilstand.

Anvendelser af Divide and Conquer-metoden:

Følgende algoritmer er baseret på konceptet Divide and Conquer-teknikken:

Binær søgning:Den binære søgealgoritme er en søgealgoritme, som også kaldes en halvintervalsøgning eller logaritmisk søgning. Det fungerer ved at sammenligne målværdien med det midterste element, der findes i et sorteret array. Efter at have foretaget sammenligningen, hvis værdien afviger, vil den halvdel, der ikke kan indeholde målet, til sidst eliminere, efterfulgt af at fortsætte søgningen på den anden halvdel. Vi vil igen overveje det midterste element og sammenligne det med målværdien. Processen bliver ved med at gentage sig, indtil målværdien er nået. Hvis vi fandt, at den anden halvdel var tom efter at have afsluttet søgningen, kan det konkluderes, at målet ikke er til stede i arrayet.Quicksort:Det er den mest effektive sorteringsalgoritme, som også er kendt som partition-exchange sort. Det starter med at vælge en pivotværdi fra et array efterfulgt af at dele resten af ​​array-elementerne i to underarrays. Partitionen laves ved at sammenligne hvert af elementerne med pivotværdien. Den sammenligner, om elementet har en større eller mindre værdi end pivoten, og sorterer derefter arrays rekursivt.Flet sortering:Det er en sorteringsalgoritme, der sorterer et array ved at foretage sammenligninger. Det starter med at opdele et array i sub-array og sorterer derefter rekursivt hver af dem. Når sorteringen er færdig, flettes dem tilbage.Nærmeste par af punkter:Det er et problem med beregningsgeometri. Denne algoritme lægger vægt på at finde ud af det nærmeste par af punkter i et metrisk rum, givet n punkter, således at afstanden mellem parret af punkter skal være minimal.Strassens algoritme:Det er en algoritme til matrixmultiplikation, som er opkaldt efter Volker Strassen. Den har vist sig at være meget hurtigere end den traditionelle algoritme, når den arbejder på store matricer.Cooley-Tukey Fast Fourier Transform (FFT) algoritme:Fast Fourier Transform-algoritmen er opkaldt efter J. W. Cooley og John Turkey. Det følger Divide and Conquer-tilgangen og pålægger en kompleksitet af O(nlogn).Karatsuba-algoritme til hurtig multiplikation:Det er en af ​​de hurtigste multiplikationsalgoritmer i den traditionelle tid, opfundet af Anatoly Karatsuba i slutningen af ​​1960 og blev udgivet i 1962. Den multiplicerer to n-cifrede tal på en sådan måde ved at reducere det til højst et-cifret.

Fordele ved Divide and Conquer

• Divide and Conquer har en tendens til med succes at løse et af de største problemer, såsom Tower of Hanoi, et matematisk puslespil. Det er udfordrende at løse komplicerede problemer, som man ikke har nogen grundlæggende idé om, men ved hjælp af del og hersk tilgangen har det mindsket indsatsen, da det arbejder på at dele hovedproblemet i to halvdele og derefter løse dem rekursivt. Denne algoritme er meget hurtigere end andre algoritmer.
• Den bruger effektivt cachehukommelse uden at optage meget plads, fordi den løser simple underproblemer i cachehukommelsen i stedet for at få adgang til den langsommere hovedhukommelse.
• Den er mere dygtig end dens modstykke Brute Force-teknik.
• Da disse algoritmer hæmmer parallelisme, involverer det ikke nogen modifikation og håndteres af systemer, der inkorporerer parallel behandling.

Ulemper ved Divide and Conquer

• Da de fleste af dens algoritmer er designet ved at inkorporere rekursion, så det nødvendiggør høj hukommelsesstyring.
• En eksplicit stak kan overforbruge pladsen.
• Det kan endda nedbryde systemet, hvis rekursionen udføres strengt større end stakken til stede i CPU'en.