Indsættelsessortering og udvælgelsessortering er to populære sorteringsalgoritmer, og deres vigtigste forskel ligger i, hvordan de udvælger og placerer elementer i en sorteret sekvens.
Udvalgssortering:
- I udvælgelsessortering er input-arrayet opdelt i to dele: en sorteret del og en usorteret del.
- Algoritmen finder gentagne gange minimumselementet i den usorterede del og ombytter det med elementet længst til venstre i den usorterede del og udvider dermed den sorterede del med ét element.
- Udvælgelsessortering har en tidskompleksitet på O(n^2) i alle tilfælde.
Indsættelsessortering:
- Ved indsættelsessortering er input-arrayet også opdelt i to dele: en sorteret del og en usorteret del.
Algoritmen opfanger et element fra den usorterede del og placerer det i den korrekte position i den sorterede del, og flytter de større elementer en position til højre.
Indsættelsessortering har en tidskompleksitet på O(n^2) i værste fald, men kan klare sig bedre på delvist sorterede arrays med en best-case tidskompleksitet på O(n).
Hovedforskelle: - Selection sort scanner den usorterede del for at finde minimumselementet, mens insertion sort scanner den sorterede del for at finde den korrekte position til at placere elementet.
Udvælgelsessortering kræver færre skift end indsættelsessortering, men flere sammenligninger.
Indsættelsessortering er mere effektiv end udvælgelsessortering, når input-arrayet er delvist sorteret eller næsten sorteret, mens markeringssortering fungerer bedre, når arrayet er meget usorteret.
Sammenfattende har begge algoritmer en lignende tidskompleksitet, men deres valg og placeringsmetoder er forskellige. Valget mellem dem afhænger af inputdataens karakteristika og de specifikke krav til det aktuelle problem.
Fordele ved indsættelsessortering:
- Enkel og let at forstå og implementere.
- Effektiv til små datasæt eller næsten sorterede data.
- In-place sorteringsalgoritme, hvilket betyder, at den ikke kræver ekstra hukommelse.
- Stabil sorteringsalgoritme, hvilket betyder, at den opretholder den relative rækkefølge af lige store elementer i input-arrayet.
Ulemper ved indsættelsessortering:
- Ineffektiv til store datasæt eller omvendt rækkefølge af data med en worst-case tidskompleksitet på O(n^2).
- Insertion sort har mange swaps, hvilket kan gøre det langsomt på moderne computere.
Fordele ved udvælgelsessortering:
- Enkel og let at forstå og implementere.
- Effektiv til små datasæt eller næsten sorterede data.
- In-place sorteringsalgoritme, hvilket betyder, at den ikke kræver ekstra hukommelse.
Ulemper ved udvælgelsessortering:
- Ineffektiv til store datasæt med en worst-case tidskompleksitet på O(n^2).
- Udvælgelsessortering har mange sammenligninger, hvilket kan gøre det langsomt på moderne computere.
- Ustabil sorteringsalgoritme, hvilket betyder, at den muligvis ikke opretholder den relative rækkefølge af lige store elementer i input-arrayet.
I denne artikel vil vi diskutere forskellen mellem indsættelsessortering og udvælgelsessortering:
Indsættelsessortering er en simpel sorteringsalgoritme, der fungerer på samme måde, som du sorterer spillekort i dine hænder. Arrayet er praktisk talt opdelt i en sorteret og en usorteret del. Værdier fra den usorterede del plukkes og placeres i den korrekte position i den sorterede del.
Algoritme:
Sådan sorterer du en matrix af størrelse n i stigende rækkefølge:
- Iterér fra arr[1] til arr[n] over arrayet.
- Sammenlign det nuværende element (nøgle) med dets forgænger.
- Hvis nøgleelementet er mindre end dets forgænger, skal du sammenligne det med elementerne før. Flyt de større elementer en position op for at gøre plads til det ombyttede element.
Nedenfor er billedet til illustration af indsættelsessortering:
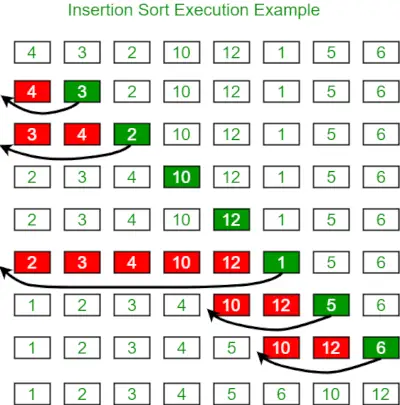
Nedenfor er programmet for det samme:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tast) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = nøgle; } } // Funktion til at udskrive et array af størrelse N void printArray(int arr[], int n) { int i; // Udskriv arrayet for (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tast) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = nøgle; } } // Funktion til at udskrive et array af størrelse N static void printArray(int arr[], int n) { int i; // Udskriv arrayet for (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Driverkode public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; Denne kode er bidraget af code_hunt> |
>
>
Python3
# Python 3 program for the insertion sort> # Function to sort an array using> # insertion sort> def> insertionSort(arr, n):> >i>=> 0> >key>=> 0> >j>=> 0> >for> i>in> range>(>1>,n,>1>):> >key>=> arr[i]> >j>=> i>-> 1> ># Move elements of arr[0..i-1],> ># that are greater than key to> ># one position ahead of their> ># current position> >while> (j>>=> 0> and> arr[j]>nøgle):> >arr[j>+> 1>]>=> arr[j]> >j>=> j>-> 1> >arr[j>+> 1>]>=> key> # Function to print an array of size N> def> printArray(arr, n):> >i>=> 0> ># Print the array> >for> i>in> range>(n):> >print>(arr[i],end>=> ' '>)> >print>(>'
'>,end>=> '')> # Driver Code> if> __name__>=>=> '__main__'>:> >arr>=> [>12>,>11>,>13>,>5>,>6>]> >N>=> len>(arr)> ># Function Call> >insertionSort(arr, N)> >printArray(arr, N)> > ># This code is contributed by bgangwar59.> |
>
>
C#
// C# program for the above approach> using> System;> class> GFG> {> >// Function to sort an array using> >// insertion sort> >static> void> insertionSort(>int>[] arr,>int> n)> >{> >int> i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tast) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = nøgle; } } // Funktion til at udskrive et array af størrelse N static void printArray(int[] arr, int n) { int i; // Udskriv arrayet for (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Driverkode statisk public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; int N = arr.Length; bidraget af Dharanendra L V> |
>
>
Javascript
> // JavaScript program for the above approach> // Function to sort an array using> // insertion sort> function> insertionSort(arr,n)> {> >let i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> tast) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = nøgle; } } // Funktion til at udskrive et array af størrelse N funktion printArray(arr,n) { let i; // Udskriv arrayet for (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Driverkode lad arr=[12, 11 , 13, 5, 6]; lad N = arr.length; // Funktion Kald insertionSort(arr, N); |
>5 6 11 12 13>
Det udvælgelsessortering algoritmen sorterer et array ved gentagne gange at finde minimumselementet (i betragtning af stigende rækkefølge) fra den usorterede del og sætte det i begyndelsen. Algoritmen opretholder to subarrays i et givet array.
- Underarrayet er allerede sorteret.
- Det resterende underarray er usorteret.
I hver iteration af udvælgelsessortering plukkes minimumselementet (i betragtning af stigende rækkefølge) fra den usorterede subarray og flyttes til den sorterede subarray.
Nedenfor er et eksempel for at forklare ovenstående trin:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>
Nedenfor er programmet for det samme:
C++
// C++ program for implementation of> // selection sort> #include> using> namespace> std;> // Function to swap two number> void> swap(>int>* xp,>int>* yp)> {> >int> temp = *xp;> >*xp = *yp;> >*yp = temp;> }> // Function to implement the selection> // sort> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array:
'; // Print the array printArray(arr, n); return 0; }> |
>
>
Java
// Java program for implementation of> // selection sort> import> java.util.*;> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995> |
>
>
Python3
# Python3 program for implementation of> # selection sort> # Function to implement the selection> # sort> def> selectionSort(arr, n):> ># One by one move boundary of> ># unsorted subarray> >for> i>in> range>(n>-> 1>):> ># Find the minimum element> ># in unsorted array> >min_idx>=> i> >for> j>in> range>(i>+> 1>, n):> >if> (arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp> |
>
>
C#
java len af array
// C# program for implementation of> // selection sort> using> System;> public> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> []arr,>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1> |
>
>
Javascript
> // Javascript program for implementation of> // selection sort> // Function to implement the selection> // sort> function> selectionSort(arr, n)> {> >let i, j, min_idx;> > >// One by one move boundary of> >// unsorted subarray> >for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127> |
>
>Produktion:
Sorted array: 11 12 22 25 64>
Tabelforskel mellem indsættelsessortering og udvalgssortering:
| Indsættelsessortering | Udvalgssortering | |
|---|---|---|
| 1. | Indsætter værdien i det forudsorterede array for at sortere værdisættet i arrayet. | Finder minimum / maksimum antal fra listen og sorterer det i stigende / faldende rækkefølge. |
| 2. | Det er en stabil sorteringsalgoritme. | Det er en ustabil sorteringsalgoritme. |
| 3. | Den bedste tidskompleksitet er Ω(N), når arrayet allerede er i stigende rækkefølge. Den har Θ(N2) i værste tilfælde og gennemsnitligt tilfælde. | For bedste tilfælde har worst case og gennemsnitlig udvælgelsessortering kompleksitet Θ(N2). |
| 4. | Antallet af sammenligningsoperationer udført i denne sorteringsalgoritme er mindre end det udførte bytte. | Antallet af sammenligningsoperationer, der udføres i denne sorteringsalgoritme, er mere end det udførte bytte. |
| 5. | Det er mere effektivt end udvælgelsessorten. | Det er mindre effektivt end indsættelsessorten. |
| 6. | Her er elementet kendt i forvejen, og vi søger efter den korrekte position for at placere dem. | Det sted, hvor elementet skal placeres, er tidligere kendt, vi søger efter elementet, der skal indsættes på den position. |
| 7. | Indsættelsessorteringen bruges når:
| Valgsorteringen bruges når
|
| 8. | Indsættelsessorteringen er adaptiv, dvs. effektiv for datasæt, der allerede er væsentligt sorteret: tidskompleksiteten er O(kn) når hvert element i inputtet ikke er mere end k steder væk fra dens sorterede position | Udvælgelsessortering er en in-place sammenligningssorteringsalgoritme |
