Denne artikel taler om Data Encryption Standard (DES), en historisk krypteringsalgoritme kendt for sin 56-bit nøglelængde. Vi udforsker dens drift, nøgletransformation og krypteringsproces og kaster lys over dens rolle i datasikkerhed og dens sårbarheder i nutidens kontekst.
Hvad er DES?
Data Encryption Standard (DES) er en blokchiffer med en 56-bit nøglelængde, der har spillet en væsentlig rolle i datasikkerheden . Datakrypteringsstandard (DES) er blevet fundet sårbar over for meget kraftige angreb, derfor er populariteten af DES blevet fundet en smule faldende. DES er en blokchiffer og krypterer data i blokke af størrelse på 64 bit hver, hvilket betyder, at 64 bits almindelig tekst går som input til DES, som producerer 64 bits chiffertekst. Den samme algoritme og nøgle bruges til kryptering og dekryptering , med mindre forskelle. Nøglen længde er 56 bit .
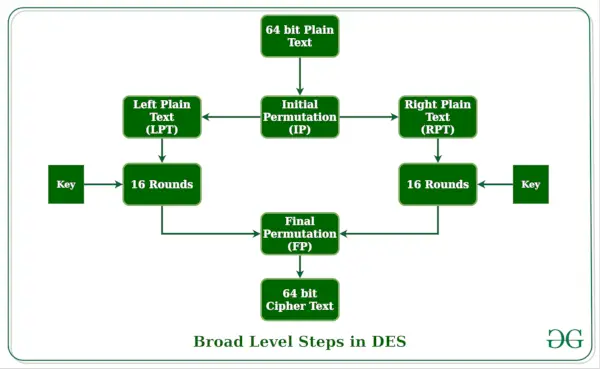
Den grundlæggende idé er vist nedenfor:
Vi har nævnt, at DES bruger en 56-bit nøgle. Faktisk består startnøglen af 64 bit. Men før DES-processen overhovedet starter, kasseres hver 8. bit af nøglen for at producere en 56-bit nøgle. Det vil sige, at bitpositionerne 8, 16, 24, 32, 40, 48, 56 og 64 kasseres.

Kassering af hver 8. bit af nøglen producerer således en 56-bit nøgle fra originalen 64-bit nøgle .
DES er baseret på de to grundlæggende egenskaber ved kryptografi : substitution (også kaldet forvirring) og transposition (også kaldet diffusion). DES består af 16 trin, som hver kaldes en runde. Hver runde udfører trinene substitution og transponering. Lad os nu diskutere de brede trin i DES.
- I det første trin overføres 64-bit almindelig tekstblokken til en initial Permutation (IP) funktion.
- Den indledende permutation udføres på almindelig tekst.
- Dernæst producerer den indledende permutation (IP) to halvdele af den permuterede blok; siger Left Plain Text (LPT) og Right Plain Text (RPT).
- Nu gennemgår hver LPT og RPT 16 runder af krypteringsprocessen.
- I sidste ende forbindes LPT og RPT igen, og en endelig permutation (FP) udføres på den kombinerede blok
- Resultatet af denne proces producerer 64-bit chiffertekst.
Initial Permutation (IP)
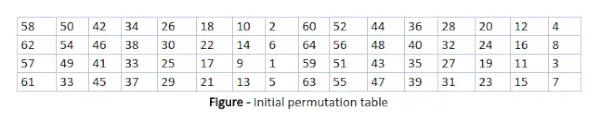
Som vi har bemærket, sker den indledende permutation (IP) kun én gang, og den sker før den første runde. Det foreslår, hvordan transponeringen i IP skal forløbe, som vist på figuren. For eksempel står der, at IP'en erstatter den første bit af den originale almindelige tekstblok med den 58. bit af den originale almindelige tekst, den anden bit med den 50. bit af den originale almindelige tekstblok, og så videre.
Dette er intet andet end jonglering af bitpositioner i den originale almindelige tekstblok. den samme regel gælder for alle de andre bitpositioner vist på figuren.
1 million tal
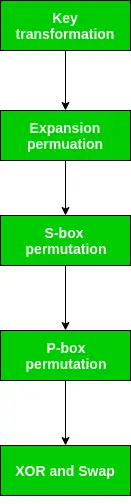
Som vi har bemærket, efter at IP er færdig, er den resulterende 64-bit permuterede tekstblok opdelt i to halve blokke. Hver halvblok består af 32 bit, og hver af de 16 runder består til gengæld af de brede trin, der er skitseret i figuren.
Trin 1: Nøgletransformation
Vi har bemærket, at den indledende 64-bit nøgle er omdannet til en 56-bit nøgle ved at kassere hver 8. bit af den indledende nøgle. Således er en 56-bit nøgle tilgængelig for hver. Fra denne 56-bit nøgle genereres en anden 48-bit undernøgle under hver runde ved hjælp af en proces kaldet nøgletransformation. Til dette er 56-bit nøglen opdelt i to halvdele, hver på 28 bit. Disse halvdele er cirkulært forskudt til venstre med en eller to positioner, afhængigt af runden.
For eksempel: hvis rundtallene 1, 2, 9 eller 16 udføres skiftet med kun én position for andre runder, det cirkulære skift udføres med to positioner. Antallet af nøglebits forskudt pr. runde er vist i figuren.

grænseflade i java
Efter et passende skift vælges 48 af de 56 bit. Fra de 48 kan vi få 64 eller 56 bit baseret på krav, hvilket hjælper os til at erkende, at denne model er meget alsidig og kan håndtere enhver række krav, der er nødvendige eller stillede til rådighed. for at vælge 48 af de 56 bit er tabellen vist i figuren nedenfor. For eksempel, efter skiftet flytter bit nummer 14 til den første position, bit nummer 17 flytter til den anden position og så videre. Hvis vi observerer tabellen, vil vi indse, at den kun indeholder 48-bit positioner. Bit nummer 18 kasseres (vi finder det ikke i tabellen), ligesom 7 andre, for at reducere en 56-bit nøgle til en 48-bit nøgle. Da nøgletransformationsprocessen involverer permutation såvel som et udvalg af en 48-bit delmængde af den originale 56-bit nøgle, kaldes den Compression Permutation.
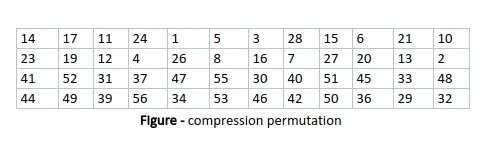
På grund af denne kompressionspermutationsteknik bruges en anden delmængde af nøglebits i hver runde. Det gør DES ikke let at knække.
Trin 2: Udvidelsespermutation
Husk, at efter den indledende permutation havde vi to 32-bit almindelig tekst områder kaldet Venstre almindelig tekst (LPT) og højre almindelig tekst (RPT). Under udvidelsespermutationen udvides RPT fra 32 bit til 48 bit. Bits permuteres også og kaldes derfor ekspansionspermutation. Dette sker, da 32-bit RPT er opdelt i 8 blokke, hvor hver blok består af 4 bit. Derefter udvides hver 4-bit blok i det foregående trin til en tilsvarende 6-bit blok, dvs. pr. 4-bit blok tilføjes yderligere 2 bits.
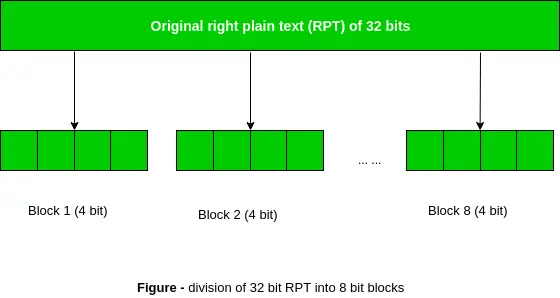
Denne proces resulterer i ekspansion såvel som en permutation af inputbit, mens der skabes output. Nøgletransformationsprocessen komprimerer 56-bit nøglen til 48 bit. Så udvider ekspansionspermutationsprocessen 32-bit RPT til 48-bit . Nu er 48-bit nøglen GRATIS med 48-bit RPT, og det resulterende output gives til næste trin, som er S-Box udskiftning .
Python
fjederst
# Python3 code for the above approach> # Hexadecimal to binary conversion> def> hex2bin(s):> >mp>=> {>'0'>:>'0000'>,> >'1'>:>'0001'>,> >'2'>:>'0010'>,> >'3'>:>'0011'>,> >'4'>:>'0100'>,> >'5'>:>'0101'>,> >'6'>:>'0110'>,> >'7'>:>'0111'>,> >'8'>:>'1000'>,> >'9'>:>'1001'>,> >'A'>:>'1010'>,> >'B'>:>'1011'>,> >'C'>:>'1100'>,> >'D'>:>'1101'>,> >'E'>:>'1110'>,> >'F'>:>'1111'>}> >bin> => ''> >for> i>in> range>(>len>(s)):> >bin> => bin> +> mp[s[i]]> >return> bin> # Binary to hexadecimal conversion> def> bin2hex(s):> >mp>=> {>'0000'>:>'0'>,> >'0001'>:>'1'>,> >'0010'>:>'2'>,> >'0011'>:>'3'>,> >'0100'>:>'4'>,> >'0101'>:>'5'>,> >'0110'>:>'6'>,> >'0111'>:>'7'>,> >'1000'>:>'8'>,> >'1001'>:>'9'>,> >'1010'>:>'A'>,> >'1011'>:>'B'>,> >'1100'>:>'C'>,> >'1101'>:>'D'>,> >'1110'>:>'E'>,> >'1111'>:>'F'>}> >hex> => ''> >for> i>in> range>(>0>,>len>(s),>4>):> >ch>=> ''> >ch>=> ch>+> s[i]> >ch>=> ch>+> s[i>+> 1>]> >ch>=> ch>+> s[i>+> 2>]> >ch>=> ch>+> s[i>+> 3>]> >hex> => hex> +> mp[ch]> >return> hex> # Binary to decimal conversion> def> bin2dec(binary):> >binary1>=> binary> >decimal, i, n>=> 0>,>0>,>0> >while>(binary !>=> 0>):> >dec>=> binary>%> 10> >decimal>=> decimal>+> dec>*> pow>(>2>, i)> >binary>=> binary>/>/>10> >i>+>=> 1> >return> decimal> # Decimal to binary conversion> def> dec2bin(num):> >res>=> bin>(num).replace(>'0b'>, '')> >if>(>len>(res)>%> 4> !>=> 0>):> >div>=> len>(res)>/> 4> >div>=> int>(div)> >counter>=> (>4> *> (div>+> 1>))>-> len>(res)> >for> i>in> range>(>0>, counter):> >res>=> '0'> +> res> >return> res> # Permute function to rearrange the bits> def> permute(k, arr, n):> >permutation>=> ''> >for> i>in> range>(>0>, n):> >permutation>=> permutation>+> k[arr[i]>-> 1>]> >return> permutation> # shifting the bits towards left by nth shifts> def> shift_left(k, nth_shifts):> >s>=> ''> >for> i>in> range>(nth_shifts):> >for> j>in> range>(>1>,>len>(k)):> >s>=> s>+> k[j]> >s>=> s>+> k[>0>]> >k>=> s> >s>=> ''> >return> k> # calculating xow of two strings of binary number a and b> def> xor(a, b):> >ans>=> ''> >for> i>in> range>(>len>(a)):> >if> a[i]>=>=> b[i]:> >ans>=> ans>+> '0'> >else>:> >ans>=> ans>+> '1'> >return> ans> # Table of Position of 64 bits at initial level: Initial Permutation Table> initial_perm>=> [>58>,>50>,>42>,>34>,>26>,>18>,>10>,>2>,> >60>,>52>,>44>,>36>,>28>,>20>,>12>,>4>,> >62>,>54>,>46>,>38>,>30>,>22>,>14>,>6>,> >64>,>56>,>48>,>40>,>32>,>24>,>16>,>8>,> >57>,>49>,>41>,>33>,>25>,>17>,>9>,>1>,> >59>,>51>,>43>,>35>,>27>,>19>,>11>,>3>,> >61>,>53>,>45>,>37>,>29>,>21>,>13>,>5>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,>7>]> # Expansion D-box Table> exp_d>=> [>32>,>1>,>2>,>3>,>4>,>5>,>4>,>5>,> >6>,>7>,>8>,>9>,>8>,>9>,>10>,>11>,> >12>,>13>,>12>,>13>,>14>,>15>,>16>,>17>,> >16>,>17>,>18>,>19>,>20>,>21>,>20>,>21>,> >22>,>23>,>24>,>25>,>24>,>25>,>26>,>27>,> >28>,>29>,>28>,>29>,>30>,>31>,>32>,>1>]> # Straight Permutation Table> per>=> [>16>,>7>,>20>,>21>,> >29>,>12>,>28>,>17>,> >1>,>15>,>23>,>26>,> >5>,>18>,>31>,>10>,> >2>,>8>,>24>,>14>,> >32>,>27>,>3>,>9>,> >19>,>13>,>30>,>6>,> >22>,>11>,>4>,>25>]> # S-box Table> sbox>=> [[[>14>,>4>,>13>,>1>,>2>,>15>,>11>,>8>,>3>,>10>,>6>,>12>,>5>,>9>,>0>,>7>],> >[>0>,>15>,>7>,>4>,>14>,>2>,>13>,>1>,>10>,>6>,>12>,>11>,>9>,>5>,>3>,>8>],> >[>4>,>1>,>14>,>8>,>13>,>6>,>2>,>11>,>15>,>12>,>9>,>7>,>3>,>10>,>5>,>0>],> >[>15>,>12>,>8>,>2>,>4>,>9>,>1>,>7>,>5>,>11>,>3>,>14>,>10>,>0>,>6>,>13>]],> >[[>15>,>1>,>8>,>14>,>6>,>11>,>3>,>4>,>9>,>7>,>2>,>13>,>12>,>0>,>5>,>10>],> >[>3>,>13>,>4>,>7>,>15>,>2>,>8>,>14>,>12>,>0>,>1>,>10>,>6>,>9>,>11>,>5>],> >[>0>,>14>,>7>,>11>,>10>,>4>,>13>,>1>,>5>,>8>,>12>,>6>,>9>,>3>,>2>,>15>],> >[>13>,>8>,>10>,>1>,>3>,>15>,>4>,>2>,>11>,>6>,>7>,>12>,>0>,>5>,>14>,>9>]],> >[[>10>,>0>,>9>,>14>,>6>,>3>,>15>,>5>,>1>,>13>,>12>,>7>,>11>,>4>,>2>,>8>],> >[>13>,>7>,>0>,>9>,>3>,>4>,>6>,>10>,>2>,>8>,>5>,>14>,>12>,>11>,>15>,>1>],> >[>13>,>6>,>4>,>9>,>8>,>15>,>3>,>0>,>11>,>1>,>2>,>12>,>5>,>10>,>14>,>7>],> >[>1>,>10>,>13>,>0>,>6>,>9>,>8>,>7>,>4>,>15>,>14>,>3>,>11>,>5>,>2>,>12>]],> >[[>7>,>13>,>14>,>3>,>0>,>6>,>9>,>10>,>1>,>2>,>8>,>5>,>11>,>12>,>4>,>15>],> >[>13>,>8>,>11>,>5>,>6>,>15>,>0>,>3>,>4>,>7>,>2>,>12>,>1>,>10>,>14>,>9>],> >[>10>,>6>,>9>,>0>,>12>,>11>,>7>,>13>,>15>,>1>,>3>,>14>,>5>,>2>,>8>,>4>],> >[>3>,>15>,>0>,>6>,>10>,>1>,>13>,>8>,>9>,>4>,>5>,>11>,>12>,>7>,>2>,>14>]],> >[[>2>,>12>,>4>,>1>,>7>,>10>,>11>,>6>,>8>,>5>,>3>,>15>,>13>,>0>,>14>,>9>],> >[>14>,>11>,>2>,>12>,>4>,>7>,>13>,>1>,>5>,>0>,>15>,>10>,>3>,>9>,>8>,>6>],> >[>4>,>2>,>1>,>11>,>10>,>13>,>7>,>8>,>15>,>9>,>12>,>5>,>6>,>3>,>0>,>14>],> >[>11>,>8>,>12>,>7>,>1>,>14>,>2>,>13>,>6>,>15>,>0>,>9>,>10>,>4>,>5>,>3>]],> >[[>12>,>1>,>10>,>15>,>9>,>2>,>6>,>8>,>0>,>13>,>3>,>4>,>14>,>7>,>5>,>11>],> >[>10>,>15>,>4>,>2>,>7>,>12>,>9>,>5>,>6>,>1>,>13>,>14>,>0>,>11>,>3>,>8>],> >[>9>,>14>,>15>,>5>,>2>,>8>,>12>,>3>,>7>,>0>,>4>,>10>,>1>,>13>,>11>,>6>],> >[>4>,>3>,>2>,>12>,>9>,>5>,>15>,>10>,>11>,>14>,>1>,>7>,>6>,>0>,>8>,>13>]],> >[[>4>,>11>,>2>,>14>,>15>,>0>,>8>,>13>,>3>,>12>,>9>,>7>,>5>,>10>,>6>,>1>],> >[>13>,>0>,>11>,>7>,>4>,>9>,>1>,>10>,>14>,>3>,>5>,>12>,>2>,>15>,>8>,>6>],> >[>1>,>4>,>11>,>13>,>12>,>3>,>7>,>14>,>10>,>15>,>6>,>8>,>0>,>5>,>9>,>2>],> >[>6>,>11>,>13>,>8>,>1>,>4>,>10>,>7>,>9>,>5>,>0>,>15>,>14>,>2>,>3>,>12>]],> >[[>13>,>2>,>8>,>4>,>6>,>15>,>11>,>1>,>10>,>9>,>3>,>14>,>5>,>0>,>12>,>7>],> >[>1>,>15>,>13>,>8>,>10>,>3>,>7>,>4>,>12>,>5>,>6>,>11>,>0>,>14>,>9>,>2>],> >[>7>,>11>,>4>,>1>,>9>,>12>,>14>,>2>,>0>,>6>,>10>,>13>,>15>,>3>,>5>,>8>],> >[>2>,>1>,>14>,>7>,>4>,>10>,>8>,>13>,>15>,>12>,>9>,>0>,>3>,>5>,>6>,>11>]]]> # Final Permutation Table> final_perm>=> [>40>,>8>,>48>,>16>,>56>,>24>,>64>,>32>,> >39>,>7>,>47>,>15>,>55>,>23>,>63>,>31>,> >38>,>6>,>46>,>14>,>54>,>22>,>62>,>30>,> >37>,>5>,>45>,>13>,>53>,>21>,>61>,>29>,> >36>,>4>,>44>,>12>,>52>,>20>,>60>,>28>,> >35>,>3>,>43>,>11>,>51>,>19>,>59>,>27>,> >34>,>2>,>42>,>10>,>50>,>18>,>58>,>26>,> >33>,>1>,>41>,>9>,>49>,>17>,>57>,>25>]> def> encrypt(pt, rkb, rk):> >pt>=> hex2bin(pt)> ># Initial Permutation> >pt>=> permute(pt, initial_perm,>64>)> >print>(>'After initial permutation'>, bin2hex(pt))> ># Splitting> >left>=> pt[>0>:>32>]> >right>=> pt[>32>:>64>]> >for> i>in> range>(>0>,>16>):> ># Expansion D-box: Expanding the 32 bits data into 48 bits> >right_expanded>=> permute(right, exp_d,>48>)> ># XOR RoundKey[i] and right_expanded> >xor_x>=> xor(right_expanded, rkb[i])> ># S-boxex: substituting the value from s-box table by calculating row and column> >sbox_str>=> ''> >for> j>in> range>(>0>,>8>):> >row>=> bin2dec(>int>(xor_x[j>*> 6>]>+> xor_x[j>*> 6> +> 5>]))> >col>=> bin2dec(> >int>(xor_x[j>*> 6> +> 1>]>+> xor_x[j>*> 6> +> 2>]>+> xor_x[j>*> 6> +> 3>]>+> xor_x[j>*> 6> +> 4>]))> >val>=> sbox[j][row][col]> >sbox_str>=> sbox_str>+> dec2bin(val)> ># Straight D-box: After substituting rearranging the bits> >sbox_str>=> permute(sbox_str, per,>32>)> ># XOR left and sbox_str> >result>=> xor(left, sbox_str)> >left>=> result> ># Swapper> >if>(i !>=> 15>):> >left, right>=> right, left> >print>(>'Round '>, i>+> 1>,>' '>, bin2hex(left),> >' '>, bin2hex(right),>' '>, rk[i])> ># Combination> >combine>=> left>+> right> ># Final permutation: final rearranging of bits to get cipher text> >cipher_text>=> permute(combine, final_perm,>64>)> >return> cipher_text> pt>=> '123456ABCD132536'> key>=> 'AABB09182736CCDD'> # Key generation> # --hex to binary> key>=> hex2bin(key)> # --parity bit drop table> keyp>=> [>57>,>49>,>41>,>33>,>25>,>17>,>9>,> >1>,>58>,>50>,>42>,>34>,>26>,>18>,> >10>,>2>,>59>,>51>,>43>,>35>,>27>,> >19>,>11>,>3>,>60>,>52>,>44>,>36>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,> >7>,>62>,>54>,>46>,>38>,>30>,>22>,> >14>,>6>,>61>,>53>,>45>,>37>,>29>,> >21>,>13>,>5>,>28>,>20>,>12>,>4>]> # getting 56 bit key from 64 bit using the parity bits> key>=> permute(key, keyp,>56>)> # Number of bit shifts> shift_table>=> [>1>,>1>,>2>,>2>,> >2>,>2>,>2>,>2>,> >1>,>2>,>2>,>2>,> >2>,>2>,>2>,>1>]> # Key- Compression Table : Compression of key from 56 bits to 48 bits> key_comp>=> [>14>,>17>,>11>,>24>,>1>,>5>,> >3>,>28>,>15>,>6>,>21>,>10>,> >23>,>19>,>12>,>4>,>26>,>8>,> >16>,>7>,>27>,>20>,>13>,>2>,> >41>,>52>,>31>,>37>,>47>,>55>,> >30>,>40>,>51>,>45>,>33>,>48>,> >44>,>49>,>39>,>56>,>34>,>53>,> >46>,>42>,>50>,>36>,>29>,>32>]> # Splitting> left>=> key[>0>:>28>]># rkb for RoundKeys in binary> right>=> key[>28>:>56>]># rk for RoundKeys in hexadecimal> rkb>=> []> rk>=> []> for> i>in> range>(>0>,>16>):> ># Shifting the bits by nth shifts by checking from shift table> >left>=> shift_left(left, shift_table[i])> >right>=> shift_left(right, shift_table[i])> ># Combination of left and right string> >combine_str>=> left>+> right> ># Compression of key from 56 to 48 bits> >round_key>=> permute(combine_str, key_comp,>48>)> >rkb.append(round_key)> >rk.append(bin2hex(round_key))> print>(>'Encryption'>)> cipher_text>=> bin2hex(encrypt(pt, rkb, rk))> print>(>'Cipher Text : '>, cipher_text)> print>(>'Decryption'>)> rkb_rev>=> rkb[::>->1>]> rk_rev>=> rk[::>->1>]> text>=> bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))> print>(>'Plain Text : '>, text)> # This code is contributed by Aditya Jain> |
>
numpy summering
>
Javascript
// Define DES key and plaintext> const key =>'0123456789abcdef'>;> const plaintext =>'Hello, world!'>;> // Perform DES encryption> const des =>new> DES(key);> const ciphertext = des.encrypt(plaintext);> // Perform DES decryption> const decrypted = des.decrypt(ciphertext);> // Print results> console.log(>'Plaintext: '>, plaintext);> console.log(>'Ciphertext: '>, ciphertext);> console.log(>'Decrypted: '>, decrypted);> // Define DES class> class DES {> >constructor(key) {> >// Initialize DES with key> >this>.key = CryptoJS.enc.Hex.parse(key);> >}> >encrypt(plaintext) {> >// Perform DES encryption on plaintext> >const encrypted = CryptoJS.DES.encrypt(> >plaintext,> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return ciphertext as hex string> >return> encrypted.ciphertext.toString();> >}> >decrypt(ciphertext) {> >// Parse ciphertext from hex string> >const ciphertextHex = CryptoJS.enc.Hex.parse(ciphertext);> >// Perform DES decryption on ciphertext> >const decrypted = CryptoJS.DES.decrypt(> >{ ciphertext: ciphertextHex },> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return decrypted plaintext as UTF-8 string> >return> decrypted.toString(CryptoJS.enc.Utf8);> >}> }> |
>
>Produktion
...60AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Produktion:
streng som en matrix
Encryption: After initial permutation: 14A7D67818CA18AD After splitting: L0=14A7D678 R0=18CA18AD Round 1 18CA18AD 5A78E394 194CD072DE8C Round 2 5A78E394 4A1210F6 4568581ABCCE Round 3 4A1210F6 B8089591 06EDA4ACF5B5 Round 4 B8089591 236779C2 DA2D032B6EE3 Round 5 236779C2 A15A4B87 69A629FEC913 Round 6 A15A4B87 2E8F9C65 C1948E87475E Round 7 2E8F9C65 A9FC20A3 708AD2DDB3C0 Round 8 A9FC20A3 308BEE97 34F822F0C66D Round 9 308BEE97 10AF9D37 84BB4473DCCC Round 10 10AF9D37 6CA6CB20 02765708B5BF Round 11 6CA6CB20 FF3C485F 6D5560AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Konklusion
Som konklusion er Data Encryption Standard (DES) en blok chiffer med en 56-bit nøglelængde, der har spillet en væsentlig rolle i datasikkerheden. Men på grund af sårbarheder er dens popularitet faldet. DES opererer gennem en række runder, der involverer nøgletransformation, ekspansionspermutation og substitution, og producerer i sidste ende chiffertekst fra klartekst. Selvom DES har historisk betydning, er det afgørende at overveje mere sikker kryptering alternativer til moderne databeskyttelsesbehov.
Ofte stillede spørgsmål
Q.1 : Hvad skal betragtes som et alternativ til DES til datakryptering?
Svar:
Til moderne datakrypteringsbehov kan du overveje at bruge stærkere krypteringsalgoritmer som AES (Avanceret krypteringsstandard).
Q.2 : Hvordan genereres 48-bit undernøglen for hver runde i DES?
Svar:
48-bit undernøglen for hver runde i DES er afledt af 56-bit nøglen gennem en proces med cirkulær forskydning og permutation, hvilket sikrer nøglediversitet.

