En NFA kan have nul, et eller mere end et træk fra en given tilstand på et givet inputsymbol. En NFA kan også have NULL-træk (træk uden inputsymbol). På den anden side har DFA et og kun et træk fra en given tilstand på et givet inputsymbol.

Trin til konvertering af NFA til DFA:

Trin 1: Konverter den givne NFA til dens tilsvarende overgangstabel
For at konvertere NFA til dens tilsvarende overgangstabel skal vi liste alle tilstande, inputsymboler og overgangsreglerne. Overgangsreglerne er repræsenteret i form af en matrix, hvor rækkerne repræsenterer den aktuelle tilstand, kolonnerne repræsenterer inputsymbolet, og cellerne repræsenterer den næste tilstand.

Trin 2: Opret DFA's starttilstand
DFA's starttilstand er sættet af alle mulige starttilstande i NFA. Dette sæt kaldes epsilon-lukningen af ​​NFA's starttilstand. Epsilon-lukningen er sættet af alle tilstande, der kan nås fra starttilstanden ved at følge epsilon(?)-overgange.

download youtube video med vlc

Trin 3: Opret DFA's overgangstabel
DFA's overgangstabel ligner NFA's overgangstabel, men i stedet for individuelle tilstande repræsenterer rækkerne og kolonnerne sæt af tilstande. For hvert inputsymbol indeholder den tilsvarende celle i overgangstabellen epsilon-lukningen af ​​sættet af tilstande opnået ved at følge overgangsreglerne i NFA's overgangstabel.

Trin 4: Opret DFA's endelige tilstande
DFA's endelige tilstande er de sæt af stater, der indeholder mindst én sluttilstand fra NFA.

Trin 5: Forenkling af DFA
DFA opnået i de foregående trin kan indeholde unødvendige tilstande og overgange. For at forenkle DFA kan vi bruge følgende teknikker:

• Fjern utilgængelige tilstande: Stater, der ikke kan nås fra starttilstanden, kan fjernes fra DFA.
• Fjern døde stater: Stater, der ikke kan føre til en endelig tilstand, kan fjernes fra DFA.
• Merge ækvivalente tilstande: Stater, der har de samme overgangsregler for alle inputsymboler, kan flettes til en enkelt tilstand.

Trin 6: Gentag trin 3-5, indtil yderligere forenkling ikke er mulig
Efter forenkling af DFA gentager vi trin 3-5, indtil yderligere forenkling ikke er mulig. Den endelige opnåede DFA er den minimerede DFA svarende til den givne NFA.

Eksempel: Overvej følgende NFA vist i figur 1.

boble sortering i algoritme

Følgende er de forskellige parametre for NFA. Q = { q0, q1, q2 } ? = (a, b) F = {q2}? (NFAs overgangsfunktion)

java hvordan man konverterer streng til int

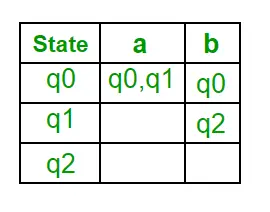
Trin 1: Q' = ? Trin 2: Q' = {q0} Trin 3: For hver tilstand i Q' skal du finde tilstandene for hvert inputsymbol. I øjeblikket er tilstanden i Q' q0, find træk fra q0 på inputsymbolet a og b ved hjælp af overgangsfunktionen i NFA og opdater overgangstabellen for DFA. ?’ (Overgangsfunktion af DFA)

Nu vil {q0, q1} blive betragtet som en enkelt tilstand. Da dens indtastning ikke er i Q', skal du tilføje den til Q'. Så Q' = { q0, { q0, q1 } } Nu, bevægelser fra tilstand { q0, q1 } på forskellige input-symboler er ikke til stede i overgangstabellen for DFA, vi vil beregne det som: ?' , a ) = ? (q0, a) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? (q0, b)? ? ( q1, b ) = { q0, q2 } Nu vil vi opdatere overgangstabellen for DFA. ?’ (Overgangsfunktion af DFA)

Nu vil {q0, q2} blive betragtet som en enkelt tilstand. Da dens indtastning ikke er i Q', skal du tilføje den til Q'. Så Q' = { q0, { q0, q1 }, { q0, q2 } } Nu, bevægelser fra tilstand {q0, q2} på forskellige inputsymboler er ikke til stede i overgangstabellen for DFA, vi vil beregne det som: ?' ( { q0, q2 }, a ) = ? (q0, a) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? (q0, b)? ? ( q2, b ) = { q0 } Nu vil vi opdatere overgangstabellen for DFA. ?’ (Overgangsfunktion af DFA)

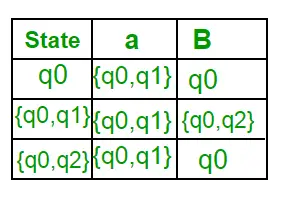
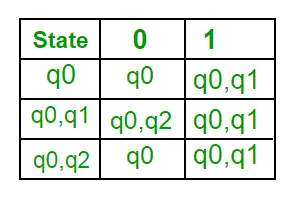
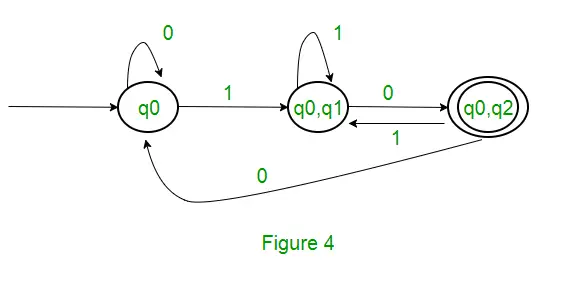
Da der ikke er genereret nogen ny tilstand, er vi færdige med konverteringen. Den endelige tilstand af DFA vil være tilstand, som har q2 som sin komponent, dvs. {q0, q2}. Følgende er de forskellige parametre for DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } ? = ( a, b ) F = { { q0, q2 } } og overgangsfunktion ?’ som vist ovenfor. Den endelige DFA for ovenstående NFA er vist i figur 2.

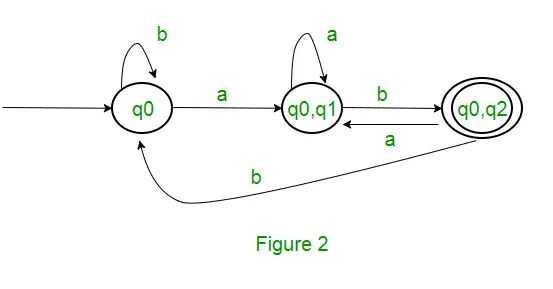
Bemærk : Nogle gange er det ikke nemt at konvertere regulære udtryk til DFA. Først kan du konvertere regulære udtryk til NFA og derefter NFA til DFA.

Spørgsmål : Antallet af tilstande i den minimale deterministiske endelige automat svarende til det regulære udtryk (0 + 1)* (10) er ____________.

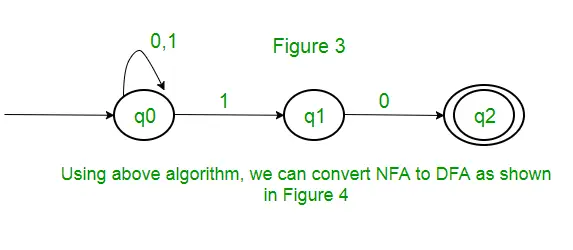
Løsning : Først vil vi lave en NFA for ovenstående udtryk. For at lave en NFA for (0 + 1)*, vil NFA være i samme tilstand q0 på inputsymbol 0 eller 1. Derefter tilføjer vi to træk til sammenkædning (q0 til q1 for 1 og q1 til q2 for 0) som vist i figur 3.

10 af 50

Denne artikel er bidraget af Sonal Tuteja.