Konvolution bruges til mange ting som at beregne afledte, detektere kanter, anvende sløringer osv. og alt dette gøres ved hjælp af en 'foldningskerne'. En foldningskerne er en meget lille matrix, og i denne matrix har hver celle et nummer og også et ankerpunkt.
Ankerpunktet bruges til at kende kernens position i forhold til billedet. Det starter i øverste venstre hjørne af billedet og bevæger sig på hver pixel sekventielt. Kernelen overlapper få pixels ved hver position på billedet. Hver pixel, der overlappes, ganges og tilføjes derefter. Og summen er sat som værdien af den aktuelle position.
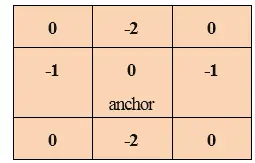
Konvolution er den proces, hvor hvert element i billedet føjes til dets lokale naboer, og derefter vægtes det af kernen. Det er relateret til en form for matematisk foldning.
I Convolution udfører matrixen ikke traditionel matrixmultiplikation, men den er angivet med *.
Antag, at der er to 3x3-matricer, en er kerne og en anden er et billedstykke. I foldning vendes rækker og kolonner i kernen, og derefter multipliceres de, og derefter foretages summering. Elementer, der er til stede i midten af matrix, dvs. i [2,2] af billedet, vil blive vægtet kombination af billedmatricen, og vægtene vil blive givet af kernen. På samme måde vil alle de andre elementer i matrixen blive vægtet, og derefter vil vægte blive beregnet.
Følgende er pseudokode til at beskrive foldningsprocessen:
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
Konvolution kan beregnes ved hjælp af multiple for loops. Men at bruge for loops forårsager en masse gentagne beregninger, og også størrelsen af billede og kerne øges. Ved hjælp af diskret Fourier-transformationsteknik kan beregning af foldning udføres hurtigt. I denne teknik konverteres hele foldningsoperationen til en simpel multiplikation.
I foldning opstår problemet, når kernen er nær kanten eller hjørnerne, fordi kernen er todimensionel.
For at overvinde disse problemer kan følgende ting gøres:
- Dem kan ignoreres
- Ekstra pixels kan oprettes nær kanterne.
Ekstra pixels kan oprettes på følgende måder:
- Dupliker kantpixel.
- Reflektere kanter
- Pixels kan kopieres fra den anden ende.
