Kortsandsynlighed er sandsynligheden for begivenheder, der involverer et sæt spillekort. Som vi ved, er sandsynlighed et af matematikkens vigtige emner, der beskæftiger sig med beregningen af muligheden for enhver begivenhed. Kort sagt er kortsandsynlighed en del af sandsynlighed, hvor vi finder sandsynligheden for at trække et kort fra bunken med kort. I denne artikel vil vi lære om kortsandsynlighed med alle detaljer om kortsandsynlighedsdiagrammet, spillekortsandsynlighed, hvordan man finder kortsandsynligheden og løste eksempler på kortsandsynlighed. Lad os begynde vores læring om emnet kortsandsynlighed.
Hvad er sandsynlighed?
Sandsynlighed er den gren af matematik, der studerer mulighederne for, at enhver begivenhed kan ske eller ej. Matematisk er intet andet end forholdet mellem antallet af gunstige udfald og det samlede antal udfald (prøverum) for en begivenhed.
Nogle af de virkelige eksempler på sandsynlighed er:
- At spille kortspil, for at finde sandsynligheden for at vinde eller tabe spillet.
- Vejrudsigt, for at forudsige regnen.
- Valgresultater, for at afgøre, om kandidaten vil vinde eller tabe.
- Eksamensresultater, for at identificere, om kandidaten vil bestå eller ikke.
Sandsynlighedsformel
Hvis E er en hændelse med stikprøverum S, og antallet af gunstige udfald er n(E), så er sandsynligheden for hændelse E, dvs. P(E) givet ved:
P(E) = n(E) / n(S)
Hvad er kortsandsynlighed?
Sandsynlighed for at trække et kort eller en samling af kort fra en bunke kaldes kortsandsynlighed. Med enkle ord kaldes sandsynlighed relateret til spillekort kortsandsynlighed. Da dette er typen af sandsynlighed, ligger den altid mellem 0 og 1. For eksempel, hvis vi skal finde sandsynligheden for at trække et es fra bunken med kort, dvs. 4/52 = 1/13 [Der er 4 esser i bunken med 52 kort].
Sæt med kort i sandsynlighed
Deck of Cards er en samling af 52 kort, der ser ud til at eksistere i tusinder af år. Deck of Cards eller spillekort anses for at stamme fra enten Indien eller Kina, det første dokumenterede bevis for disse kort er fundet i 9thårhundredes Kina under Tang-dynastiet. Disse kort lignede nutidens kort og også opdelt i fire kulører, men navnet og symbolet på disse kulører er forskellige, dvs. mønter, strenge af mønter, myriader og myriader af tiere.
I moderne tid kommer disse kort i forskellige designs og er opdelt i fire farver, nemlig Spade (♠), Kølle (♣), Hjerte (❤) og Diamant (◆). For et enkelt valgt kort er prøverummet 52, dvs. det samlede antal udfald for et enkelt valgt kort fra et kortspil er 52.
n(S) for spil kort = 52
Typer af kort i en bunke
Ethvert sæt kort kan klassificeres på mange måder, nogle af parametrene, som kort kan klassificeres på er:
- Baseret på farver
- Baseret på dragter
Lad os forstå denne klassificering i detaljer som følger:
Baseret på farver
Baseret på farver kan et sæt kort klassificeres i to kategorier,
- Røde kort
- Sorte kort
I alt 52 kort er fordelt ligeligt i røde og sorte kort, hvilket betyder, at der er 26 røde kort og 26 sorte kort i bunken.
Baseret på dragter
Der er fire farver i bunken med kort, der er:
fejl: kunne ikke finde eller indlæse hovedklassen
- Hjerter (❤)
- Diamanter (◆)
- Klubber (♣)
- Spar (♠)
Bortset fra disse er der endnu en klassifikation af kort, baseret på rangeringen af kort:
- Es
- Nummerkort
- Ansigtskort
Es
Es er et sådant kort, som enten er det vigtigste eller mindst vigtige baseret på spillet. Dette kort A skrevet på det, og hver farve har et af sådanne kort, dvs. fire es-kort.
Nummerkort
Fra 2 til 10 er der 9 kort pr. farve, så der er i alt 36 sådanne kort.
Ansigtskort
Billede kort, som navnet antyder, indeholder en figur eller ansigt af figuren på kortet. Der er tre kort i hver kulør, dvs. knægt, dronning, konge. Der er således i alt 12 billedkort.
Alle disse klassifikationer kan ses i følgende tabel.
| Kortsæt (52 kort) | ||||
|---|---|---|---|---|
| Farvede kort | Sorte kort (26 kort) | Røde kort (26 kort) | ||
| Jakkesæt | Spade (13 kort) | Klub (13 kort) | Hjerte (13 kort) | Diamant (13 kort) |
| Ansigtskort (12 kort i et spil og 3 kort i hver farve) | K (konge) | K (konge) | K (konge) | K (konge) |
| Q (dronning) | Q (dronning) | Q (dronning) | Q (dronning) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Nummerkort (36 kort i et spil og 9 kort i en kulør) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Es-kort (4 kort i dæk og 1 kort i en kulør) | A (Es) | A (Es) | A (Es) | A (Es) |
Kortspil kort
Følgende diagram repræsenterer klassificeringen af bunken med spillekort:
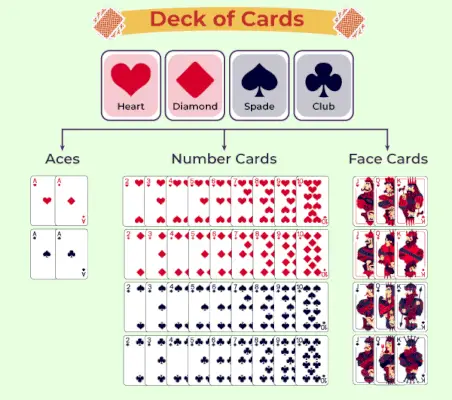
Sandsynlighed for spillekort
Nogle af de almindelige hændelser i kortsandsynligheder er diskuteret i følgende tabel:
| Event E for at trække kort | Sandsynlighed P(E) |
|---|---|
| Et es | P(E) = 4/52 = 1/13 |
| En konge | P(E) = 4/52 = 1/13 |
| Et nummerkort | P(E) = 36/52 = 9/13 |
| Et ansigtskort | P(E) = 12/52 = 3/13 |
| Et spadekort | P(E) = 13/52 = 1/4 |
| Et rødt kort | P(E) = 26/52 = 1/2 |
Hvordan finder man sandsynligheden for kort?
Trin til at finde sandsynligheden for begivenheder, der involverer kort, er de samme som alle de andre sandsynligheder, der er givet som følger:
Trin 1: Find først antallet af gunstige resultater fra det givne spørgsmål.
Trin 2: Find derefter det samlede antal resultater.
Trin 3: Anvend sandsynlighedsformlen for at finde kortsandsynligheden.
Eksempel: Hvad er sandsynligheden for at trække et es fra et sæt kort?
Svar:
Her er E tilfældet med at trække et es-kort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = trække et es-kort fra bunken = 4 (Der er 4 es-kort i 1 dæk)
P(E) = n(E) / n(S) = 4/52
P(E) = 1/13
Sandsynlighed for at trække et es-kort = 1/13
Eksempel på spørgsmål om kortsandsynlighed
Opgave 1: Hvad er sandsynligheden for at trække følgende kort fra et sæt kort?
(i) en spade
(ii) et sort kort
(iii) et nummerkort
Løsning:
(i) Her er E tilfældet med at trække et sparkort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = trække et spadekort fra bunken = 13 (Der er 13 kort i hver farve i 1 bunke)
java-tegn til strengP(E) = n(E) / n(S) = 13/52
P(E) = 1/4
Sandsynlighed for at trække en spade = 1/4
(ii) Her er E tilfældet med at trække et sort kort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = trække et sort kort fra bunken = 26 (Der er 26 sorte kort i 1 bunke)
P(E) = n(E) / n(S) = 26/52
P(E) = 1/2
Sandsynlighed for at trække et sort kort = 1/2
(iii) Her er E tilfældet med at trække et nummerkort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = trække et talkort fra bunken = 36 (Der er 36 talkort i 1 dæk)
P(E) = n(E) / n(S) = 36 / 52
P(E) = 9/13
Sandsynlighed for at trække et talkort = 9/13
Opgave 2: Hvad er sandsynligheden for at trække følgende kort fra et sæt kort?
(i) En konge eller et sort kort
(ii) Et kort med rødt og es
Løsning:
(i) Her er E begivenheden med at trække en konge eller et sort kort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = trække en konge eller et sort kort fra bunken = 26 + 2 = 28 (Der er 26 sorte kort, hvor 2 er konge og resterende 2 konger af sort i 1 bunke)
P(E) = n(E) / n(S) = 28/52
P(E) = 7/13
Sandsynlighed for at trække en konge eller et sort kort = 7/13
(ii) Her er E tilfældet med at trække et rødt og et es-kort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = trække et rødt og es-kort fra bunken = 2 (Der er 26 røde kort, hvor 2 er es-kort)
Ifølge spørgsmålet skal trukket kort være både rødt og es. Derfor er n(E) = 2
P(E) = n(E) / n(S) = 2/52
P(E) = 1/26
Sandsynlighed for at trække et rødt kort med es = 1/26
Opgave 3: Hvad er sandsynligheden for at trække følgende kort fra et sæt kort?
(i) Et ikke-klubkort
(ii) Et ikke-ansigtskort
Løsning:
(i) Her er E tilfældet med at trække et ikke-klubkort
Samlet antal udfald i et kortspil n(S) = 52
q1 q2 q3 q4Antal gunstige udfald = n(E) = trække et ikke-klubkort fra bunken = 39 (Der er 13 køller i 1 dæk, ikke-dæk = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39/52
P(E) = 3/4
Sandsynlighed for at trække et ikke-klubkort = 3/4
(ii) Her er E tilfældet med at trække et ikke-ansigtskort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = at trække et ikke-ansigtskort fra bunken = 40 (Der er 12 billedkort i 1 dæk, ikke-dækket = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40/52
P(E) = 10/13
Sandsynlighed for at trække et ikke-klubkort = 10/13
Opgave 4: Hvad er sandsynligheden for at trække et kort, der hverken er rødt eller et billedkort?
Løsning:
Her er E tilfælde af at trække et hverken rødt eller et billedkort
Samlet antal udfald i et kortspil n(S) = 52
Antal gunstige udfald = n(E) = trækker hverken rødt eller et billedkort fra bunken.
I alt røde kort = 26
Der er i alt 12 billedkort i et kortspil, men 6 røde billedkort er allerede fjernet. Så resterende billedkort = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/52
P(E) = 8/13
Sandsynlighed for at trække et hverken rødt eller et billedkort = 8/13
Opgave 5: Hvad er sandsynligheden for at trække to kort fra et sæt kort med udskiftning, når det første kort er hjerte og andet kort er ruder?
Løsning:
Sandsynlighed for at trække det første kort som hjerte = 13/52
Efter at have trukket det første kort, fjernes kortet.
Sandsynlighed for at trække det andet kort som diamant = 13/51
Sandsynlighed for at trække det første kort som hjerte og det andet som ruder = (13/52) × (13/51)
Sandsynlighed for at trække det første kort som hjerte og det andet som ruder = 13/204
Ofte stillede spørgsmål om kortsandsynlighed
1. Hvad er kortsandsynlighed?
Sandsynligheden for at trække et kort fra bunken med kort kaldes kortsandsynlighed.
2. Angiv typerne af jakkesæt i et sæt kort.
Der er fire typer kulører i et sæt kort. De er:
- Hjerter
- Diamanter
- Spar
- Klubber
3. Hvad er prøvepladsen til bunken med kort, når der trækkes et kort fra bunken?
Prøvepladsen til et sæt kort, når et kort trækkes, indeholder 52 udfald.
4. Skriv formlen for at finde sandsynlighed.
Formlen for at finde sandsynlighed er givet ved:
Sandsynlighed for hændelse = Antal gunstige hændelser / Samlet antal udfald
ELLER
P(E) = n(E) / n(S)
5. Hvor mange ansigtskort er der i et sæt kort?
Der er 12 billedkort i et sæt kort.
