I denne tutorial vil vi udforske en af krypteringsmetoderne kaldet Caesar Cipher. Det er en del af kryptografi.
Introduktion
I denne teknik erstattes hvert tegn med et bogstav, der er bestemt med et bestemt nummer, det er senere eller før alfabetet. For eksempel - Alfabet B erstattes af to positioner nede D. D ville blive F og så videre. Denne metode er opkaldt efter populære friktionsfigurer Julius Cæsar, som brugte den til at kommunikere med embedsmænd.
Der er en algoritme, der bruges til at implementere det. Lad os forstå følgende.
Funktion af Caesar Cipher Algorithm
Denne algoritme består af et par funktioner, der er angivet nedenfor.
- Denne teknik er ret enkel at anvende kryptering.
- Hver tekst erstattes af det faste antal positioner ned eller op med alfabetet.
- Det er en simpel type erstatnings-ciffer.
Der kræves en heltalsværdi for at definere hver sidstnævnte af teksten, der er blevet flyttet ned. Denne heltalsværdi er også kendt som skiftet.
understreg ved hjælp af css
Vi kan repræsentere dette koncept ved hjælp af modulær aritmetik ved først at omsætte bogstavet til tal, ifølge skemaet, A = 0, B = 1, C = 2, D = 3…….. Z = 25.
Følgende matematiske formel kan bruges til at flytte n bogstav.
Hvordan dekrypteres?
Dekrypteringen er den samme som kryptering. Vi kan oprette en funktion, der vil udføre skift i den modsatte vej for at dekryptere den originale tekst. Vi kan dog bruge chifferens cykliske egenskab under modulet.
flette sortering java
Cipher(n) = De-chipher(26-n)
Den samme funktion kan bruges til dekryptering. I stedet vil vi ændre skiftværdien, således at skift = 26 - skift.
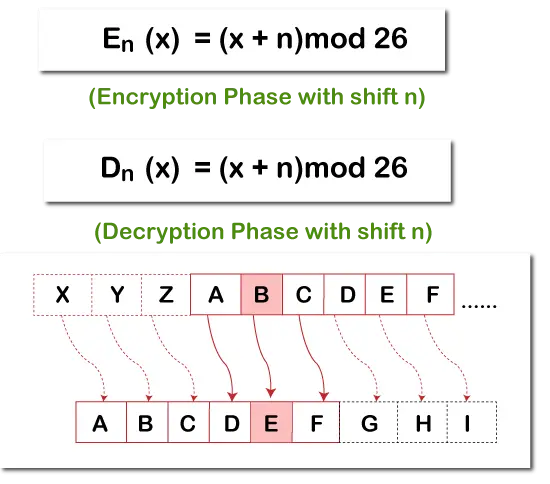
Lad os forstå følgende eksempel -
Eksempel -
1 ud af 1000
def encypt_func(txt, s): result = '' # transverse the plain txt for i in range(len(txt)): char = txt[i] # encypt_func uppercase characters in plain txt if (char.isupper()): result += chr((ord(char) + s - 64) % 26 + 65) # encypt_func lowercase characters in plain txt else: result += chr((ord(char) + s - 96) % 26 + 97) return result # check the above function txt = 'CEASER CIPHER EXAMPLE' s = 4 print('Plain txt : ' + txt) print('Shift pattern : ' + str(s)) print('Cipher: ' + encypt_func(txt, s))
Produktion:
Plain txt : CEASER CIPHER EXAMPLE Shift pattern : 4 Cipher: HJFXJWsHNUMJWsJCFRUQJ
Ovenstående kode har krydset tegnet ad gangen. Det overførte hvert tegn i henhold til reglen afhængigt af proceduren for kryptering og dekryptering af teksten.
Vi har defineret få specifikke sæt positioner, der genererede en krypteringstekst.
Brud på Cæsar Cipher Algorithm
Vi kan hacke krypteringsteksten på forskellige måder. En af måderne er Brute Force teknik, hvilket involverer at prøve alle mulige dekrypteringsnøgler. Denne teknik er ikke så hård og kræver ikke meget indsats.
Lad os forstå følgende eksempel.
Eksempel -
msg = 'rGMTLIVrHIQSGIEWIVGIEWIV' #encrypted msg LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' for k in range(len(LETTERS)): transformation = '' for s in msg: if s in LETTERS: n = LETTERS.find(s) n = n - k if n <0: n="n" + len(letters) transformation="transformation" letters[n] else: s print('hacking k #%s: %s' % (k, transformation)) < pre> <p> <strong>Output:</strong> </p> <pre> Hacking k #25: rHNUMJWrIJRTHJFXJWHJFXJW </pre> <h2>Transposition Cipher</h2> <p>Transposition cipher algorithm is a technique where the alphabet order in the plaintext is rearranged to form a cipher text. This algorithm doesn't support the actual plain text alphabets.</p> <p>Let's understand this algorithm using an example.</p> <p> <strong>Example -</strong> </p> <p>We will take the simple example called columnar transposition cipher where we write the each character in the pain text in horizontal with specified alphabet width. The vertically written texts are cipher, which create a completely unlike cipher text.</p> <p>Let's take a plain text, and apply the simple columnar transposition technique as shown below.</p> <img src="//techcodeview.com/img/python-tutorial/89/caesar-cipher-python-2.webp" alt="Caesar Cipher in Python"> <p>We placed the plain text horizontally and the cipher text is created with vertical format as: <strong>hotnejpt.lao.lvi.</strong> To decrypt this, the receiver must use the same table to decrypt the cipher text to plain text.</p> <p> <strong>Code -</strong> </p> <p>Let's understand the following example.</p> <pre> def split_len(sequence, length): return [sequence[i:i + length] for i in range(0, len(sequence), length)] def encode(k, plaintxt): order = { int(val): n for n, val in enumerate(k) } ciphertext = '' for index in sorted(order.ks()): for part in split_len(plaintxt, len(k)): try:ciphertext += part[order[index]] except IndexError: continue return ciphertext print(encode('3214', 'HELLO')) </pre> <p> <strong>Explanation -</strong> </p> <p>In the above code, we have created a function named <strong>split_len(),</strong> which spitted the pain text character, placed in columnar or row format.</p> <p>The <strong>encode()</strong> method created the cipher text with a key specifying the number of columns, and we have printed each cipher text by reading through each column.</p> <h4>Note - The transposition technique is meant to be a significant improvement in crypto security. Cryptanalyst observed that re-encrypting the cipher text using same transposition cipher shows better security.</h4> <hr></0:> Transposition Cipher
Transposition chifferalgoritme er en teknik, hvor alfabetets rækkefølge i klarteksten omarrangeres til at danne en chiffertekst. Denne algoritme understøtter ikke de faktiske almindelige tekst-alfabeter.
streng som array
Lad os forstå denne algoritme ved hjælp af et eksempel.
Eksempel -
Vi vil tage det simple eksempel kaldet columnar transposition cipher, hvor vi skriver hvert tegn i smerteteksten i vandret med specificeret alfabetbredde. De lodret skrevne tekster er chiffer, hvilket skaber en helt ulig chiffertekst.
Lad os tage en almindelig tekst og anvende den enkle søjleformede transponeringsteknik som vist nedenfor.
js base64 afkode

Vi placerede den almindelige tekst vandret, og chifferteksten oprettes med lodret format som: hotnejpt.lao.lvi. For at dekryptere dette skal modtageren bruge den samme tabel til at dekryptere chifferteksten til almindelig tekst.
Kode -
Lad os forstå følgende eksempel.
def split_len(sequence, length): return [sequence[i:i + length] for i in range(0, len(sequence), length)] def encode(k, plaintxt): order = { int(val): n for n, val in enumerate(k) } ciphertext = '' for index in sorted(order.ks()): for part in split_len(plaintxt, len(k)): try:ciphertext += part[order[index]] except IndexError: continue return ciphertext print(encode('3214', 'HELLO')) Forklaring -
I ovenstående kode har vi lavet en funktion ved navn split_len(), som spyttede smertetekstkarakteren, placeret i søjle- eller rækkeformat.
Det indkode() metode skabte krypteringsteksten med en nøgle, der angiver antallet af kolonner, og vi har udskrevet hver krypteringstekst ved at læse hver kolonne igennem.
