Binært talsystem er et talsystem, der bruges til at repræsentere forskellige tal ved kun at bruge to symboler 0 og 1. Ordet binær er afledt af ordet bi, som betyder to. Derfor kaldes dette talsystem for binært talsystem. Det binære talsystem er således et system, der kun har to symboler.
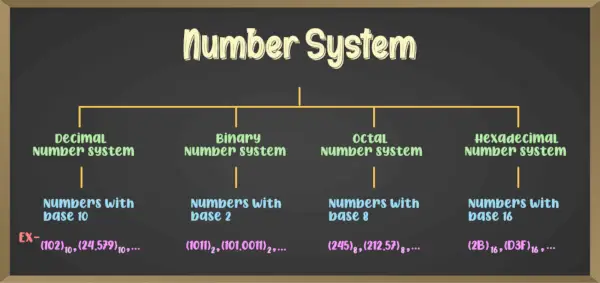
Der er generelt forskellige typer af talsystemer, og blandt dem er de fire vigtigste,
- Binært talsystem (talsystem med base 2)
- Oktaltalsystem (talsystem med base 8)
- Decimaltalsystem (talsystem med grundtal 10)
- Hexadecimalt talsystem (talsystem med base 16)
Her skal vi kun lære om binært talsystem. Dette talsystem er meget nyttigt til at forklare opgaver til computeren. I det binære talsystem har vi to tilstande 0 og 1, og disse to tilstande er repræsenteret af to tilstande af en transistor. Hvis strømmen går gennem transistoren, så læser computeren 1, og hvis strømmen er fraværende fra transistoren, læser den 0. Alternerende strømmen læser computeren således det binære talsystem. Hvert ciffer i det binære talsystem kaldes en bit.
I denne artikel vil vi lære om det binære talsystem, konverteringen af det binære talsystem, den binære tabel, driften af binære tal, eksempler og andre i detaljer.
Indholdsfortegnelse
- Binært talsystem
- Binær taltabel
- Binær til decimal konvertering
- Decimal til binær konvertering
- Aritmetiske operationer på binære tal
- 1'er og 2'er komplement til et binært tal
- Brug af binært talsystem
- Eksempel på binært talsystem
Binært talsystem
Binært talsystem er det talsystem, hvor vi bruger to cifre 0 og 1 til at udføre alle de nødvendige operationer. I det binære talsystem har vi en base på 2. Grundlaget for det binære talsystem kaldes også radixen af talsystem .
I et binært talsystem repræsenterer vi tallet som,
- (11001)2
I ovenstående eksempel er der givet et binært tal, hvor grundtallet er 2. I et binært talsystem kaldes hvert ciffer bit. I ovenstående eksempel er der 5 cifre.
Binær taltabel
| Decimaltal | Binært tal | Decimaltal | Binært tal |
|---|---|---|---|
| 1 | 001 | elleve | 1011 |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | femten | 1111 |
| 6 | 110 | 16 | 10.000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 konverter str til int | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 | 1010 | tyve | 10100 |
Binær til decimal konvertering
Et binært tal konverteres til et decimaltal ved at gange hvert ciffer i det binære tal med potensen af enten 1 eller 0 til den tilsvarende potens af 2. Lad os overveje, at et binært tal har n cifre, B = an-1…en3-en2-en1-en0. Nu er det tilsvarende decimaltal angivet som
D = (a n-1 ×2 n-1 ) +…+(a 3 ×2 3 ) + (a 2 ×2 2 ) + (a 1 ×2 1 ) + (a 0 ×2 0 )
Lad os gennemgå et eksempel for at forstå konceptet bedre.
Eksempel: Konverter (10011) 2 til et decimaltal.
Løsning:
Det givne binære tal er (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Derfor er det binære tal (10011)2er udtrykt som (19)10.
Decimal til binær konvertering
Et decimaltal konverteres til et binært tal ved at dividere det givne decimaltal med 2 løbende, indtil vi får kvotienten som 1, og vi skriver tallene fra nedad til opad.
Lad os gennemgå et eksempel for at forstå konceptet bedre.
Eksempel: Konverter (28) 10 til et binært tal.
Løsning:
Derfor (28)10er udtrykt som (11100)2.
Aritmetiske operationer på binære tal
Vi kan nemt udføre forskellige operationer på binære tal. Forskellige aritmetiske operationer på det binære tal inkluderer,
- Binær tilføjelse
- Binær subtraktion
- Binær multiplikation
- Binær division
Lad os nu lære om det samme i detaljer.
Binær tilføjelse
Resultatet af tilføjelsen af to binære tal er også et binært tal. For at opnå resultatet af tilføjelsen af to binære tal, skal vi tilføje tallet for de binære tal for ciffer. Tabellen tilføjet nedenfor viser reglen for binær addition.
| Binært tal (1) | Binært tal (2) | Tilføjelse | Bære |
|---|---|---|---|
| 0 | 0 | 0 | 0 omdøbe mappe linux |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Binær subtraktion
Resultatet af subtraktionen af to binære tal er også et binært tal. For at opnå resultatet af subtraktionen af to binære tal, skal vi trække tallet fra de binære tal fra for ciffer. Tabellen tilføjet nedenfor viser reglen for binær subtraktion.
| Binært tal (1) | Binært tal (2) | Subtraktion | Låne |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Binær multiplikation
Multiplikationsprocessen for binære tal ligner multiplikationen af decimaltal. Reglerne for at gange vilkårlige to binære tal er givet i tabellen,
| Binært tal (1) | Binært tal (2) | Multiplikation |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Binær division
Det divisionsmetode for binære tal svarer til metoden med decimaltalsdelingsmetoden. Lad os gennemgå et eksempel for at forstå konceptet bedre.
Eksempel: Divide (101101) 2 af (110) 2
Løsning:
1'er og 2'er komplement til et binært tal
- 1's komplement til et binært tal opnås ved at invertere cifrene i det binære tal.
Eksempel: Find 1-komplementet af (10011) 2 .
arraylist metoder
Løsning:
Givet binært tal er (10011)2
Nu, for at finde dets 1-komplement, skal vi invertere cifrene i det givne tal.
Således er 1's komplement af (10011)2er (01100)2
- 2's komplement til et binært tal opnås ved at invertere cifrene i det binære tal og derefter ved at tilføje 1 til den mindst signifikante bit.
Eksempel: Find 2'erens komplement af (1011) 2 .
Løsning:
Givet binært tal er (1011)2
For at finde 2'erens komplement skal du først finde dets 1'er komplementet, dvs. (0100)2
Nu, ved at tilføje 1 til den mindst signifikante bit, får vi (0101)2
Derfor er 2'erens komplement af (1011)2er (0101)2
Brug af binært talsystem
Binære talsystemer bruges til forskellige formål, og den vigtigste anvendelse af det binære talsystem er,
- Binært talsystem bruges i al digital elektronik til at udføre forskellige operationer.
- Programmeringssprog bruger binært talsystem til kodning og afkodning af data.
- Binært talsystem bruges i datavidenskab til forskellige formål osv.
Læs mere,
- Binær formel
- Forskellen mellem decimal- og binære talsystemer
Eksempel på binært talsystem
Eksempel 1: Konverter decimaltal (98) 10 til binær.
Løsning:
Således binært tal for (98)10er lig med (1100010)2
Eksempel 2: Konverter binært tal (1010101) 2 til decimaltal.
Løsning:
Givet binært nummer, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 × 26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Således binært tal (1010101)2er lig med (85)10i decimalsystem.
Eksempel 3: Divide (11110) 2 af (101) 2
Løsning:
Eksempel 4: Tilføj (11011) 2 og (10100) 2
Løsning:
Derfor (11011)2+ (10100)2= (101111)2
Eksempel 5: Træk fra (11010) 2 og (10110) 2
Løsning:
Derfor (11010)2– (10110)2= (00100)2
Eksempel 6: Multiplicer (1110) 2 og (1001) 2 .
Løsning:
Således (1110)2× (1001)2= (1111110)2
Ofte stillede spørgsmål om binært talsystem
Hvad er et binært talsystem?
Binært talsystem er et af de fire talsystem, der bruges til at repræsentere tallene med kun to cifre, 0 og 1. I binært talsystem kaldes cifrene 'bits'. Binært talsystem bruges af computere til at udføre forskellige beregninger.
Hvad er en B det?
En bit i binært talsystem er defineret som individuelle cifre, der har værdien '0' eller '1'.
Hvad er en Nibble?
En gruppe på fire cifre kaldes Niblle.
Hvad er binær værdi af 10?
Binær værdi på 10 er (1010)2
Hvad er typer af talsystemer?
Der findes forskellige typer af talsystemer, og nogle af dem er,
- Binært talsystem
- Oktaltalssystem
- Decimaltalssystem
- Hexadecimalt talsystem
Hvordan beregner man binære tal?
Binære tal beregnes ud fra dimaltal ved at dividere decimaltallet med 2 og skrive resten. Derefter arrangerer vi alle de resterende fra nyeste til ældste for at få det binære tal.
Hvordan tilføjer man binære tal?
Binære tal tilføjes ved at bruge formlerne skrevet nedenfor,
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (bær 1)






